مدلسازی آشفتگی با استفاده از روش‌های RANS

Turbulence Modeling Using RANS Methods

روش‌های RANS براساس میانگین‌گیری معادلات ناویر استوکس توسعه یافته‌اند. معادلات ناویر-استوکس جامع‌ترین معادلات حاکم موجود بر حرکت سیالات می‌باشد که شامل یک معادله پیوستگی، سه معادله ممنتم (برای جریان‌های سه بعدی) و یک معادله انرژی (برای جریان‌های تراکم پذیر یا همراه با انتقال حرارت) می‌باشد. پدیده آشفتگی به نوعی در معادلات ناویر استوکس مستتر است و می‌توان آن را بصورت تغییرات و نوسانات سرعت در هر لحظه درک نمود. در واقع ترم وابستگی جریان به زمان (با اصل ثابت بودن شرایط مرزی یا خصوصیات جریان نسبت به زمان) اصلی‌ترین مبین آشفتگی جریان می‌باشد.

همانطور که می دانیم iشفتگی (توربولانس) عبارتست از عدم تبعیت توده‌های متوالی در یک جریان از یک خط شناخته شده جریان، به عبارت دیگر هر توده جریان ممکن است بصورت اتفاقی موقعیت محلی خود را در هر یک از جهات تغییر دهد و بصورت یقین نمی توان موقعیت آنرا مشخص نمود. به عبارت دیگر آشفتگی ذاتا پدیده‌ای ناپایا و وابسته به زمان است. آنچه که مورد سئوال واقع می‌شود اینست که در صورت عدم اطمینان به موقعیت هر توده سیال چگونه می توان راجع به کل جریان تصمیم گرفت؟ پاسخ آنست که می توان بصورت آماری و با دقت قابل ملاحظه‌ای در مورد متوسط وقایع درون جریان نظر داد و بهمین شکل در مورد وقایع آن پیش بینی و آنگاه تصمیم‌گیری کرد. درواقع این پاسخ اساس و فلسفه توسعه روش‌های Reynold-Average Navier-Stokes: RANS می‌باشد.

روش برخورد RANS با جریان‌های آشفته (توربولانت) در مهندسی کاربرد فراوان دارد، تفکیک خصوصیات میدان جریان به دو بخش مقدار متوسط و مقدار ناشی از نوسانات جریان است که برای اولین بار توسط رینولدز برای جریان‌های تراکم ناپذیر پیشنهاد شد. در این روش هر کمیت دلخواه را بصورت زیر می نویسند:

متوسط گیری زمانی رینولدز برای جریان‌های تراکم ناپذیر.

با توجه به تعریف مقدار میانگین رینولدز، معادلات پیوستگی و ممنتم برای جریان‌های تراکم ناپذیر را می‌توان بصورت زیر بازنویسی نمود. مهمترین نکته در معادلات زیر مفهوم لزجت گردابه‌ای (Eddy Viscosity) در فرض بوزینسک است که به لزجت آشقتگی (Turbulence Viscosity) یا همان μt می‌باشد. هدف نهایی تمامی مدل‌های آشفتگی RANS در محاسبه هرچه دقیق‌تر این متغیر، μt، است و تلاش بر اینست که به کمترین خطا بتوان آن را بدست آورد. نکته دیگر وابستگی کامل دقت محاسبه متغیرهای به کیفیت شبکه تولید شده است. بنابراین بطور خلاصه برای شبیه سازی هرچه دقیقتر جریان‌های آشفته لازمست اولا از مدل‌های آشفتگی مناسب و ثانیا از شبکه با کیفیت استفاده کنیم.

بازنویسی معادلات پیوستگی و ممنتم برای جریان‌های تراکم ناپذیر به فرم RANS.

هدف اصلی مدل‌های توسعه یافته در روش‌های RANS محاسبه هرچه دقیق‌تر μt بصورت مستقیم یا غیر مستقیم می‌باشد. این مدل‌های آشفتگی می‌توانند بصورت‌های مختلف بیان شوند. تعداد معادلات دیفرانسیل بیانگر نوع مدل آشفتگی است. همانطور که پیشتر اشاره شده است مدلهایی که فاقد هر نوع معادله دیفرانسیلی می‌باشد با عنوان مدل جبری شناخته می‌شود. مدلهایی که دارای یک معادله دیفرانسیلی هستند در گروه مدلهای یک معادله‌ای قرار می‌گیرند و در نهایت مدلهایی که دارای دو معادله هستند مدلهای دو معادله‌ای هستند. البته مدلهایی وجود دارد که بیش از دو معادله دیفرانسیلی را در خود جای‌ داده‌اند.

مدلهای جبری (مدل طول تداخل پرانتل، مدل جبری فون کارمن)
مدلهای یک معادله‌ای(مدل یک معادله‌ای پرانتل، مدل گلاشکو-امونز، مدل ولف-شاتین، مدل برادشاو، مدل بالدوین-بارث، مدل اسپالارت-آلماراس)
مدلهای دو معادله‌ای (K-ε، K-ω، q-f، K-z، K-ζ و K-kl-ω)
مدلهای چند معادله‌ای (هانژالیک:3، روها:5، چو:9، دیویدوف: 10، کولاوادین:20)

در مدل‌های جبری آشفتگی معادله دیفرانسیل ظاهر نمی‌شود. بهترین نمونه این نوع مدل‌ها مدل طول تداخل پرانتل است که کاربرد بسیار گسترده‌ای دارد. مدل انرژی پرانتل نیز که از طریق حل معادلات انتقال بیان می‌گردد، یک مدل یک معادله‌ای مناسب در زمان خود بود و بهمین شکل مدل دو معادله‌ای کولموگروف نیز مدلی مناسب بود. بدیهی است که با بالا رفتن تعداد معادلات، وقت و هزینه بیشتری باید جهت حل هر مدل صرف نمود. به هر صورت معیارهای مدل‌های آشفتگی (مدل های توربولانس) خوب عبارتند از:

گستره عملکرد آن مناسب باشد.
ثابتهایی که در اصل استفاده شده است باید ثابتهای مرسوم باشد.
تعداد معادلاتی که مدل به معادلات جریان استفاده می‌کند باید حداقل باشد.
پاسخهای آن قابل قبول باشد (انطباق تئوری با آزمایش).
از جهت دقت کامپیوتر و نیروی فکر اقتصادی باشد.
بطور کلی ساده باشد.

مدل آشفتگی اسپالارت-آلماراس (Spalart-Allmaras Turbulence Model)

مدل اسپالارت-آلماراس (Spalart-Allmaras) یک مدل آشفتگی یک معادله‌ای و از روش‌های RANS است. پاسخ‌های این مدل محلی بوده (یعنی اینکه حل معادله در یک نقطه هیچ ربطی به حل نقاط دیگر ندارد) و بنابراین با انواع شبکه‌های دامنه محاسباتی معادله ناویر-استوکس بصورت باسازمان و یا بی‌سازمان در فضاهای دو و سه بعدی سازگار است. پاسخ‌های این مدل با سرعت نسبتاً خوبی برای حالت پایا همگرا می‌شوند. همچنین پیچیدگی اعمال شرائط مرزی دیواره و جریان آزاد در این مدل ناچیز است. پاسخ‌های مدل در نقطه‌ای که بوسیله کاربر مشخص می‌شود، انتقال آرام به آشفتگی نسبتاً همواری دارد. همچنین این مدل از توانایی کافی برای کالیبره شدن روی لایه‌های ترکیبی دو بعدی، دنباله‌ها و لایه‌های مرزی صفحه تخت که برای ساختن بلاکهایی برای حل جریان‌های آئرودینامیک در نظر گرفته شده است، برخوردار می‌باشد. پاسخ‌های این مدل بطور رضایت بخشی گرادیان فشار در لایه مرزی را پیشگویی می‌کند. از طرفی نتایج بدست آمده در نزدیکی دنباله‌ها نیز رضایت بخش است و بعنوان کاندیدای خوب برای جریان‌های پیچیده‌تر همچون سیستم‌های برازا یا اتصال بال و بدنه ظاهر شده است.

تولید و کالیبره کردن مدل

برای بدست آوردن این مدل، از یک مدل یک معادله‌ای بسیار ساده برای کاربرد در جریانهای برشی آزاد تا پیچیده‌ترین معادله برای حالت جریانهای لزج گذرنده از بدنه‌های جامد و با نواحی آرام استفاده شده است. در حالیکه هر اثر فیزیکی که به میدان جریان اضافه می‌شود، ترم‌های جدیدی نیزبه مدل اضافه شده و کالیبره می‌شوند. این ترمها بوسیله زیرنویس‌های مشترک درثابتها وتوابع درگیر مشخص شده‌اند. قابل توجه است که ثابتها بطوری بی‌بعد شده‌اند که توابع از درجه 1باشد. این مدل بصورت مستقیم و بی واسطه لزجت آشفتگی را محاسبه می‌کند. از آنجایی که هیچ معادله انتقال دقیقی برای محاسبه لزجت آشفتگی وجود ندارد، این مدل تقریبا ترم به ترم و با استفاده از کارهای تجربی مد توسعه یافته و حتی از فرایندهای کلاسیک ساختن و کالیبره کردن مدل در جریان‌های آشفته همگن، پیروی نشده است. این مهم بخاطر اینست که اولا مدل ابتدائی با یک معادله، بقدری ساده است که خودبخود به رفتار آشفتگی همگن می‌رسد و ثانیا تاکید سازندگان این مدل بر جریان‌های واقعی آئرودینامیک و علاقه اندک آنها به جریان‌های آشفته همگن بود. البته هر چند اسپالارت و آلماراس تاکیدی روی جریانهای آشفته همگن نداشتند اما در عین حال بطور کامل درگیر چالشهای موجود در جریانهای آشفته غیر همگن نیز نشدند. این دو با گرداوری مقادیر بر گرفته از میدان جریان متوسط و‌ لزجت سینماتیکی آشفتگی، νt، که ثابت گالیلین را بهمراه دارد، این مدل را استخراج کردند. آنها همچنین جریان‌های برشی آزاد در رینولندهای بالا که بواسطه آن لزجت مولکولی نقش تاثیرگذاری در معادله انتقال نخواهد داشت را در نظر گرفتند و دلیل آنها برای این فرض اینست که در چنین جریان‌هایی، اطلاعات و همچنین انرژی، از گردابه‌های بزرگ به گردابه‌های کوچک منتقل می‌شود. که فرآیند محاسبه آن در زیر نشان داده شده است.

این مدل برای جریان‌ها در نزیدیک دیواره برای اعداد رینولدز بالا و پایین (بخصوص برای لایه بافر) کالیبره شده است. به همین جهت پاسخ‌های بسیار مناسبی در حل میدان جریان در نزدیکی دیواره می‌دهد. همچنین وونگ (Wong) در سال 1999 این مدل را برای جریان‌های مافوق صوت همراه با جدایش نیز کالیبره نمود. توابع ft1 و ft2 برای کالیبره کردن نواحی انتقالی جریان آرام به آشفته استخراج شده‌اند و اگر جریان کاملا آشفته باشد می‌توان آن‌ها را صفر در نظر گرفت. Cw و fw نیز به ترتیب ثوابت و توابع کالیبره کننده مدل در نزدیکی مرزهای جامد بوده که برای رینولدزهای بالا و پایین بدست توسعه یافته‌اند.

فرمولاسیون مدل آشفتگی اسپالارت-آلماراس (Spalart-Allmaras Turbulence Model)

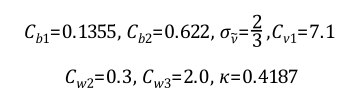
جزئیات بیشتر در مورد مدل‌های آشفتگی یک معادله‌ای و بخصوص مدل اسپالارت-آلماراس (Spalart-Allmaras) در فایل پیوست زیر ارائه شده است.

مدل‌های آشفتگی یک معادله‌ای دریافت

ویژگی‌های مهم مدل آشفتگی اسپالارت-آلماراس (Spalart-Allmaras)

مهمترین ویژگی‌های مدل آشفتگی اسپالارت-آلماراس (Spalart-Allmaras) عبارتند از:

این مدل اساسا برای حل مسائل آئرودینامیک توسعه یافته است.
این مدل پاسخ‌های خوبی برای جریان در لایه مرزی بخصوص لایه‌های مرزی درگیر با گرادیان فشار معکوس ارائه می‌کند.
محبوبیت این مدل برای حل میدان جریان در توربوماشین‌ها در حال افزایش است.
برای حل مناسب جریان با رینولدزهای کم با استفاده از مدل اسپالارت-آلماراس در لایه مرزی لازمست اندازه شبکه به قدری ریز شود تا 1~(+Y) یا به عبارت دیگر وای پلاس حدودا یک باشد.
البته در نرم افزار Fluent تمهیداتی اندیشه شده است تا ضمن غیرحساس کردن رفتار مدل در نزدیکی دیواره در حالت کلی 30>+Y>یک ( وای پلاس بین یک تا 30 ) نیز جواب‌های قابل قبولی از این مدل گرفته شود.
بطور کلی با 10 تا 15 المان در لایه مرزی می‌توان پاسخ‌های مناسبی دریافت نمود.
این مدل هنوز برای کاربردهای عمومی صنعتی کالیبره نشده است و برای جریان‌های برشی آزاد مثل انواع جریان‌های جت به نسبت خطای بیشتری تولید می‌کند. همچنین برای پیش بینی نرخ اتلاف آشفتگی ایزوتروپیک و همگن خیلی نمی‌توان روی این مدل حساب باز کرد!

آموزش تئوری و استفاده از مدل اسپالارت-آلماراس در نرم افزار Fluent همراه با حل یک مسئله

مدل آشفتگی دو معادله‌ای K-Epsilon

مدل‌های توربولانس (آشفتگی) K-ε: Epsilon یکی دیگر از خانواده روش‌های RANS، متداول‌ترین و کاربردی‌ترین مدل‌های دومعادله‌ای و یا حتی در کل مدل‌های آشفتگی هستند. خانواده مدل‌ آشفتگی K-Epsilon از دو معادله انتقالی برای حل انرژی جنبشی آشفتگی، K، و نرخ اتلاف گردابه‌ای ε، یا همان Epsilon استفاده می‌کنند. مهمترین مدل‌های معروف خانواده K-ε مدل‌های K-Epsilon Standard، K-Epsilon RNG و K-Epsilon Realizable می‌باشند. فرمولاسیون کلی مدل‌های فوق شبیه به هم می‌باشد اما در کل از تفاوتهای عمده زیر برخوردار هستند:

1- از ترم‌های متفاوتی در معادله انتقالی برای محاسبه نرخ اتلاف گردابه‌ای، ε، استفاده می‌کنند.

2- ثابت‌های استفاده شده در آن‌ها با یکدیگر متفاوت می‌باشد.

3-مقادیر اعداد پرانل آشفته مورد استفاده در معادلات K و ε با یکدیگر متفاوت می‌باشد.

در زبان عامیانه می‌توان به خانواده مدل K-Epsilon لقب آچار فرانسه مدل‌های آشفتگی را داد چرا که در اغلب مسائل سیالاتی از کیفیت و دقت حداقلی برخوردار هستند و می‌توان از آن‌ها استفاده نمود. دلایل و ملاحظات‌ مربوط به توسعه مدل‌های خانواده K-Epsilon در کنار کاربردها و مقایسه بین آن‌ها همیشه مورد توجه دانشجویان و مهندسان در طی تمامی دوره‌های آموزشی بوده از این رو در این پست سعی شده تا این موارد تشریح گردد.

مدل آشفتگی K-Epsilon Standard

اساس مدل آشفتگی K-Epsilon Standard مدل پیشنهادی Launder-Spalding می‌باشد. پایداری، اقتصادی و برخورداری از دقت حداقلی برای گستره وسیعی از کاربردهای صنعتی، دلایل اصلی محبوبیت این مدل است. این مدل یک مدل نیمه تجربی بوده و مشتقات معادلات مدل بر پایه ملاحظات پدیده شناسی و تجربیات اکتسابی استخراج شده است. در این مدل معادله انتقالی K از یک معادله دقیق ریاضی استخراج شده است در حالیکه ε از دستکاری تجربی معادله دقیق پایه مرتبط بدست آمده است.

لازم به توضیح است مدل K-Epsilon Standard با فرض جریان کاملا آشفته (Fully Turbulent Flow) توسعه یافته است. به همین خاطر شبیه سازی ناحیه انتقالی آرام به آشفته در این مدل جایگاهی ندارد. مطلب دیگر اینکه از اثرات لزجت ملکولی در توسعه این مدل صرف نظر شده است. بنابراین اولین نکته در استفاده از این مدل بهره گیری از آن صرفا برای حل میدان‌های جریان کاملا آشفته می‌باشد که البته فرض بسیار متداولی در اکثر مسائل مهندسی سیالات به شمار می‌رود. نکته دیگر اینکه این مدل برای جریان‌های با عدد رینولدز بالا مناسب می‌باشد. پس از شناسایی نقاط قوت و ضعف این مدل بود که مدل‌های اصلاح شده بیشتری از جمله مدل‌های K-Epsilon RNG و K-Epsilon Realizable توسعه یافتند.

فرمولاسیون مدل توربولانس K-Epsilon Standard.

در معادلات انتقالی K و ε، ترم‌های مهم درگیر در سمت راست معادلات عبارتند از:

Gk: ترم تولید انرژی ناشی از گرادیان‌های سرعت متوسط جریان

Gb: ترم تولید انرژی ناشی از بویانسی (برای جریان‌های بدون جاذبه و انتقال حرارت صفر می‌باشد)

Ym: ترم تولید انرژی جنبشی ناشی از اثرات تراکم پذیری جریان (برای جریان‌های تراکم ناپذیر صفر است)

σk و σε: اعداد پرانتل متناسب با k و ε هستند.

Sk و Sε: هم ترم‌های چشمه قابل تعریف توسط اپراتور هستند.

در معادلات مدل مذکور ثابت Cμ و همچنین سایر ثابت‌ها براساس نتایج آزمایشگاهی متنوع و متعددی برای جریان‌های مختلف نظیر جریان در لایه مرزی، لایه‌های مختلط (Mixixng Layer)، جریان جت‌ها و غیره بدست آمده است. اگر چه این ثوابت در دامنه وسیعی از کاربردها پاسخ‌های قابل قبولی می‌دهند اما در صورت نیاز می‌توان آن‌ها را تغییر داد. البته توصیه می‌شود جز در مواردی که اشراف کامل به پدیدیه‌های جریان، رفتار مدل در شبیه سازی آن‌ها و همچنین نوع اثر گذاری ثوابت بر نتایج دارید ثابت‌های فوق را تغییر دهید در غیر این صورت حتی فکرش را هم نکنید!!

مدل آشفتگی K-Epsilon RNG

مدل توربولانس K-Epsilon RNG از خانواده RANS، یکی ازمدل‌های بهبود یافته K-Epsilon بر اساس مدل K-Epsilon Standard می‌باشد. در این مدل نسبت به مدل Standard بهینه‌ سازی های زیر انجام شده است.

این مدل از یک ترم اضافه، Rε، در معادله انتقال ε استفاده می‌کند که دقت آن را دشبیه سازی جریان‌های آشفته با کرنش‌های سریع (Rapidly Strained) افزایش می‌دهد
در مدل K-Epsilon RNG اثر چرخش جریان روی لزجت آشفتگی لحاظ شده است در نتیجه شاهد افزایش دقت شبیه سازی در شبیه سازی جریان‌های چرخشی هستیم
تئوری مدل مذکور یک رابطه تحلیلی برای عدد پرانتل آشفته پیشنهاد می‌کند در حالیکه در مدل استفاندارد این مقدار یک عدد ثابت می‌باشد.
در حالیکه مدل K-Epsilon Standard یک مدل مناسب برای رینولدزهای بالاست، مدل RNG یک رابطه دیفرانسیلی مبتنی بر حل تحلیلی برای لحاظ نمود لزجت مؤثر، μeff، در رینولدزهای پایین را ارائه می‌کند.

قابلیت‌های فوق مدل RNG را نسبت به Standard دقیق‌تر و کاربردی‌تر ساخته است. مدل K-Epsilon RNG از معادلات ناویر-استوکس لحظه‌ای (Instantaneous Navier-Stokes) و با استفاده از تکنیک‌های ریاضی معروف به Re-Normalized Group: RNG به دست آمده است.

تفاوت اصلی بین مدل K-Epsilon RNG با مدل K-Epsilon Standard در ترم Rε است که به منظور افزایش عملکرد بهتر مدل در تخمین دقیق‌تر اثرات کرنش‌های سریع و انحنای خطوط جریان (Streamline Curveture) نسبت به مدل Standard می‌باشد. همانطور که در ابتدای این بحث نیز گفته شد ثوابت این مدل نیز با مدل Standard متفاوت بوده و مقدار آن‌ها در فرمولاسیون‌های مرتبط مشخص شده است.

بطور کلی در جریان‌های دورانی و یا چرخشی، آشفتگی متأثر از مقدارمتوسط سرعت دورانی یا چرخشی است. مدل K-Epsilon RNG قادر است تا با تقریب مناسبی اثرات این پدیده‌ها را روی لزجت آشفتگی لحاظ کند. در واقع این مدل لزجت آشفتگی نهایی را بصورت تابعی از لزجت آشفتگی اولیه محاسبه شده توسط معادلات انتقال K و ε همراه با خصوصیات چرخش و دوران محاسبه می‌کند که بصورت (μt=μt0(αs, Ω, k/ε تعریف می‌شود. αs به ثابت چرخش (Swirl Constant) معروف است و مقدار مناسب آن بسته به این که جریان دارای چرخشی ملایم (Mildly Swirling) و یا اینکه غالبا چرخش (Swirl Dominate) باشد تغییر می‌کند. معمولا برای چرخش ملایم αs=0.07 و برای دوران یا چرخش‌های قویتر بیشتر است. این مقادیر برای تمامی جریان‌های دورانی سه بعدی، چرخشی (Swirling) و متقارن محوری (Axymetric) صادق است. Ω نیز عدد چرخش (Swirl Number) می‌باشد و نکته مهم در مورد آن اینست که استفاده از مدل آشفتگی K-Epsilon RNG برای مقادیر Ω کمتر از 0.5 پیشنهادی می‌شود.

مدل آشفتگی K-Epsilon Realizable

مدل K-Epsilon Realizable از یک رابطه جایگزین برای محاسبه لزج آشفتگی استفاده می‌کند. همچنین در این مدل یک معادله انتقالی تصحیح شده مبتنی بر معادله دقیق انتقال حداقل مربعات نوسانات سرعت برای محاسبه نرخ اتلاف، ε؛ بکار گرفته شده است. اصطلاح Realizable به این مفهوم است که مدل مذکور شرایط و قیدهای ریاضی مشخصی را روی تنش‌های رینولدز سازگار با جریان‌های آشفته ارضاء می‌کند که این مقابلیت در هیچ یک از دیگ رمدل‌های K-Epsilon وجود ندارد. با ترکیب رابطه بوزینسک و تعریف لزجت آشفتگی، مدل Realizable همانند مدل RNG در شبیه‌سازی جریان‌های همراه با خطوط جریان منحنی قوی‌تر، گردابه‌ها و دوران، بهتر از مدل Standard عمل می‌کند.

از آنجائیکه این مدل نسبتا جدید است شناخت دقیقی از تمام رفتارهای آن در حل میدان‌های جریان‌های متفاوت آشفته وجود ندارد. با این حال ادعا بر اینست که این مدل نسبت به دو مدل دیگر K-Epsilon عملکرد بهتری از خود بر جای گذاشته است. بطور کلی مشخصات مدل K-Epsilon Realizable عبارتند از:

این مدل از یک فرمولاسیون جدید وابسته به رینولدز برای محاسبه Cμ استفاده می‌کند.
معادله انتقال جدید پیشنهادی برای ε، براساس میانگین مربعات نوسانات سرعت به دست آمده است.

فرمولاسیون مدل توربولانس K-Epsilon Realizable.

در معادلات بالا می‌توان دید که Cμ تابعی از نرخ‌های دوران و کرنش متوسط، سرعت زاویه‌ای سیستم‌های دورانی میدان آشفتگی K و ε می‌باشد. برای هر سه مدل K-Epsilon، معادله انتقال انرژی جنبشی آشفتگی، K، تقریبا یکسان است (بجز اختلافات جزئی در تعاریف و مقادیر ثابت‌ها)، اما معادلات انتقال نرخ اتلاف، ε، بطور قابل توجهی متفاوت هستند که در مدل K-E Realizable نیز شاهد آن هستیم. یکی از مهمترین این تفاوت‌ها اینست که اثری از ترم Gk در معادله انتقال ε نیست. اعتقاد بر اینست که این فرمولاسیون انتقال انرژی اسپکترال را بهتر بیان می‌کند. اثر ترم Gb یا همان بویانسی روی معادلات انتقال K به مراتب روشن‌تر و دقیق‌تر از معادلات انتقال ε است و در نرم افزارهایی مثل فلوئنت (Ansys Fluent) بطور پیش فرض از لحاظ نمودن آن صرف نظر می‌شود. اگر کاربر خود بخواهد می‌تواند آن را فعال کند. نکته دیگر آنکه ترم سوم سمت راست معادله هیچ‌گونه حالت تکینگی (سینگولاریتی) ندارد.

مدل مذکور برای کاربردهای بسیاری صحه گذاری شده است. جریان‌های برشی همگن دورانی، جریان‌های آزاد شامل جت‌ها و لایه‌های مختلط، جریان در کانال‌ها، لایه‌های مرزی و همچنین جدایی جریان از سطح (Separation) از جمله آنه‌ها هستند. برای تمامی این حالات عملکرد این مدل نسبت به مدل Standard بطور قابل توجهی بهتر بوده مخصوصا اگر مسأله شامل ناهنجاری‌های جت دوار (Round Jets) نیز باشد.

یکی از نقاط ضعف این مدل در حالتهایی است که دامنه محاسابتی شامل نواحی مختلف و متشکل از جریان دورانی و جریان انتقالی یا به عبارت دیگر Multiple Reference Frame: MRF باشد. در این شرایط احتمال اینکه مقادیر لزجت آشفتگی محاسبه شده توسط این مدل غیر فیزیکی باشد بسیار زیاد است چراکه این مدل اثرات متوسط دوران را در کل دامنه محاسباتی -از جمله نواحی دارای صرفا حرکت انتقالی- لحاظ می‌کند. به هر حال بخاطر طبیعت اصلاحات انجام شده در این مدل، بهره گیری از آن برای شبیه سازی مسائل متشکل از چندین دامنه محاسباتی با ویژگی‌های متفاوت، مستلزم رعایت احتیاط‌های لازم می‌باشد.

آموزش تئوری و استفاده از انواع مدل‌های K-E در نرم افزار Fluent همراه با حل یک مسئله

مدل آشفتگی دو معادله‌ای K-Omega

مدل K-ω: Omega یکی از مدل‌های متداول آشفتگیدو معادله‌ای است که از دو معادله انتقالی برای انرژی جنبشی آشفتگی (K) و اتلاف ویژه (ω) -که اندازه آشفتگی را مشخص می‌کند- تشکیل شده است. عمدتا مدل‌های آشفتگی K-Omega بر اساس مدل پایه ویلکاکس، K-Omega Wilcox، توسعه یافته‌اند. لازم به ذکر است بر روی مدل K-Omega Wilcox اصلاحاتی برای کاربرد در رینولدز پایین صورت گرفته است. البته بدون اصلاحات یاد شده نیز می‌توان از مدل K-Omega در زیر لایه لزج (Viscous Sublayer) استفاده نمود. در واقع اصلاحات مذکور اساسا برای مشاهده قله (Peak) انرژی جنبشی آشفتگی مشاهده شده توسط روش‌های عددی DNS (اینجا) در فاصله بسیار نزدیک به دیواره، به مدل پایه ویلکاکس اضافه شده‌اند. بعلاوه افزودن ترم‌های اصلاحی بر فرآیند انتقالی جریان آرام به آشفته تأثیر گذار بوده و می‌توانند شروع لایه مرزی آشفته روی دیواره را به تأخیر بیاندازند. بطور کلی استفاده از ترم‌های اصلاحی عدد رینولدز پایین در مدل‌های K-Omega پیشنهاد نمی‌شود (به عنوان مثال در نرم افزار Fluent آپشنی جهت استفاده از اصلاحات عدد رینولز پایین وجود دارد) و بجای آن بهتر است از مدل‌های پیشرفته‌تر و کالیبره شده‌تر برای انتقال لایه مرزی آرام به آشفته استفاده نمود.

هدف ما در این بخش معرفی سه مدل معروف خانواده مدل‌های توربولانس K-Omega می‌باشد که در دنیای CFD بسیار متداول و شناخته شده هستند. مدل‌های K-Omega Standard، K-Omega Baseline: BSL و K-Omega Shear Stress Transport: SST سه مدل معروف خانواده K-ω هستند. تمامی مدل‌های فوق از فرم‌های مشابهی در معادلات انتقالی برای انرژی جنبشی آشفتگی (K) و ω برخوردارند. مدل‌های BSL و SST مدل‌های جدیدتر و مدرن‌تری نسبت به مدل K-Omega Standard بوده و در جهت افزایش پایداری و همگرایی حل و همچنین افزایش دقت محاسبه لزجت (ویسکوزیته) آشفتگی ناشی از اثرات انتقالی تنش برشی آشفتگی (تنها در مدل SST) روی آن‌ها اصلاحاتی انجام شده است.

مدل آشفتگی K-Omega Standard

شالوده اصلی مدل K-omega Standard همان مدل K-Omega Wilcox می‌باشد که از ترم‌هایی برای لحاظ نمودن اثرات اعداد رینولدز پایین، تراکم‌پذیری و گسترش جریان برشی برخوردار است. یکی از نقاط ضعف کلی مدل K-Omega Wilcox و مدل‌های برگرفته از آن، حساس بودن فرآیند حل به مقادیر K و ω در بیرون از لایه برشی (حساسیت حل به جریان آزاد) می‌باشد که باعث کاهش پایداری و مشکل شدن همگرایی فرآیند حل این مدل‌ها می‌شود. اگر چه در نرم‌افزارهای تجاری معروف و قابل اعتمادی نظیر Fluent سعی شده تا حد امکان از این حساسیت‌ها کاسته شود اما همچنان شاهد اثرات قابل توجه جریان‌های برشی آزاد بر فرآیند حل هستیم. مدل K-Omega Standard یک مدل تجربی مبتنی بر معادلات انتقال برای انرژی جنبشی آشفتگی (K) و نرخ اتلاف ویژه (ω) می‌باشد. لازم به توضیح است که نرخ اتلاف ویژه را می‌توان بصورت ε/K نیز تعریف نمود. همراه با توسعه مدل K-ω طی سال‌های متمادی، ترم‌هایی نیز به معادلات اصلی این مدل اضافه شده‌اند که دقت مدل را برای پیش‌بینی تنش‌های آزاد جریان بهبود بخشیده‌اند. بطور کلی معادلات اصلی انتقال K و ω و همچنین سایر روابط در مدل استاندارد K-Omega عبارتند از:

اصلی‌ترین ترم‌های معادلات انتقال مدل K-Omega که در بالا نشان داده شده است عبارتند از:

Gk: انرژی جنبشی ناشی از گردابه‌های متوسط

Gω: ترم تولید ω

Γk و Γω: انتشار مؤثر K و ω

Sk و Sω: ترم‌های چشمه قابل تعریف توسط کاربر

σk و σω: اعداد پرانتل مرتبط با K و ω

همچنین مهمترین ویژگی‌های مدل K-Omega Standard عبارتند از:

عملکرد بسیار خوب در شبیه سازی لایه‌های مرزی محدود به دیواره (Wall-Bounded Boundary Layer)، جریان‌های برشی آزاد و همچنین جریان‌های با رینولدز پایین
مناسب برای شبیه سازی جریان‌های لایه مرزی پیچیده تحت گرادیان فشار منفی و یا جدایش نظیر آئرودینامیک خارجی و جریان در توربوماشین‌ها
قابل استفاده برای شبیه سازی ناحیه انتقالی بین جریان آرام و آشفته و همچنین جدایش جریان (هر چند در تعیین محل وقوع ناحیه انتقالی و یا جدایی جریان خیلی دقیق نیست)

مدل آشفتگی K-Omega Baseline: BSL

همانطور که پیشتر گفته شد، مهمترین مشکل مدل K-Omega Wilcox، حساسیت شدید آن به شرایط جریان آزاد می‌باشد. در همین راستا مدل K-Omega BSL توسط منتر (Menter) و با راهکارترکیب مؤثر فرمولاسیون دقیق و پایدار مدل K-Omega در ناحیه نزدیک دیواره با قابلیت استقلال از جریان آزاد مدل K-Epsilon در مرزهای دوردست (Far Field) توسعه یافته و ارائه گردید. بطور خلاصه هنگام استفاده از این مدل، مدل K-Epsilon در مرزهای دوردست به مدل K-Omega در نزدیکی دیواره تبدیل می‌شود. اساس مدل K-Omega BSL شبیه مدل K-Omega Standard می‌باشد و البته از تفاوت‌های زیر نیز برخوردار است:

1- در این مدل، مدل استاندارد K-Omega و مدل استاندارد K-E یا به عبارت دیگر Transformed K-ε، در یک تابع ترکیب وزنی، F1، ضرب شده و با یکدیگر جمع می‌شوند. معادله ترکیب طوری طراحی شده است که در نزدیکی دیواره 1 باشد تا پاسخ‌ها کاملا با مدل استاندارد K-Omega یکی باشد و برعکس در مرز دوردست صفر در نظر گرفته می‌شود تا پاسخ‌ها کاملا از مدل K-Epsilon استخراج گردد.

2- مدل K-Omega BSL از یک ترم اضافی مشتق انتشار متقابل (Cross-Deffusion) در معادله انتقال ω استفاده می‌کند.

3-ثابت‌های مدل با هم متفاوت هستند.

قابل توجه است که در معادلات و ثوابت فوق از ذکر دوباره معادلات و ثابت‌های مشترک بین این مدل و مدل K-Omega Standard خود داری شده است. به عنوان خاتمه کلام در مورد مدل K-Omega BSL تنها به این موضوع بسنده می‌شود که موارد کاربرد و دقت این مدل تقریبا با موارد کاربرد و دقت مدل K-Omega Standard یکی است اما از عملکرد بهتری در پایداری و همگرایی حل برخوردار می‌باشد.

مدل آشفتگی K-Omega Shear Stress Transport: SST

مدل SST علاوه بر اینکه تمامی اصلاحات مدل BSL را با خود به همراه دارد، از روابط اضافی برای محاسبات انتقال تنش برشی آشفتگی در تعریف لزجت آشفتگی استفاده می‌کند. علی رغم مزایای مدل BSL نسبت به مدل استاندارد K-Omega، آن مدل همچنان در تخمین مناسب شروع و میزان جدایش جریان از سطوح هموار ضعیف عمل می‌کند چرا که هر دو مدل یاد شده برای تعیین مقدار انتقال تنش برشی محاسبه‌ای انجام نمی‌دهند. این مهم باعث پیش‌بینی بیش از اندازه لزجت گردابه‌ای می‌شود. برای حل این مشکل، در مدل SST برای رسیدن به رفتار مناسب مدل در محاسبه ناحیه انتقالی می‌توان از یک مقید کننده فرمولاسیون لزجت گردابه‌ای استفاده نمود. در واقع این رابطه مهمترین اختلاف بین مدل SST با سایر مدل‌های خانواده K-Omega می‌باشد.

همانطور که در بالا به آن اشاره شد فرمولاسیون SST همانند فرمولاسیون BSL می‌باشد اما تفاوت‌هایی در محاسبه لزجت گردابه‌ای بین این دو مدل وجود دارد و روابط متفاوت مورد استفاده در مدل SST در بالا نشان داده شده است. در روابط فوق S اندازه نرخ کرنش بوده و *α نیز از همان رابطه مشابه در مدل K-Omega Standard محاسبه می‌شود. به هر حال مهمترین ویژگی‌های این مدل عبارتند از:

برای محاسبه ناحیه انتقالی بین جریان آرام و آشفته بسیار مناسب است.
در تخمین جدایی جریان از سطوح صاف بطور قابل توجهی از سایر مدل‌های خانواده K-Omega بهتر عمل می‌کند.
با توجه به خصوصیات فوق مناسب‌ترین مدل (بین مدل‌های خانواده K-Epsilon و K-Omega) از لحاظ پیش‌گویی ضریب پسا/درگ (Drag) بویژه ضریب درگ اصطکاکی در سرعت‌های کم و جدایش جریان می‌باشد.
این مدل هم همانند سایر مدل‌های خانواده K-Omega نسبت به جریان‌های برشی آزاد حساس بوده و از صلاحیت کمی برای شبیه سازی چنین جریان‌هایی برخوردار است.
نرم افزار Fluent با انجام اصلاحاتی بر روی این مدل، امکان شبیه سازی پدیده یخ زدگی روی سطوح را فراهم نموده است که برای دریافت جزئیات بیشتر می‌توانید به راهنمای این نرم افزار مراجعه کنید.

بطور کلی پیشنهاد می‌شود (البته نه در همه موارد) برای همگرایی بهتر، از نتایج حاصل از حل مدل K-Epsilon Standard به عنوان شرایط اولیه انجام محاسبات توسط مدل‌های K-Omega استفاده نمود.

آموزش تئوری و استفاده از انواع مدل‌های K-W در نرم افزار Fluent همراه با حل یک مسئله

مدل آشفتگی سه معادله‌ای Transition K-Kl-Omega

مدل آشفتگی K-Kl-ω: Omega گذرا که بیشتر با عنوان مدل K-Kl-Omega معروف است یکی از جدیدترین مدل‌های آشفتگی است که اولین بار توسط والترز (Walters) و کاکلجت (Cokljat) در سال 2008 به دنیای CFD معرفی گشته که به عنوان مدل استاندارد شناخته می‌شود. فارست (Furst) فرم تصحیح شده مدل مذکور را در سال 2013 معرفی نمود. از فرم استاندارد این مدل در نرم افزار Fluent و از فرم‌های استاندارد و تصحیح شده آن در نرم افزار OpenFOAM استفاده می‌شود.

مدل K-Kl-ω با هدف پیش‌بینی توسعه لایه مرزی و شروع ناحیه انتقال آرام به آشفته توسعه یافته است. با استفاده از این مدل می‌توان به آدرس دقیقی از محل پیدایش ناحیه انتقال آرام به آشفته دست یافت و لایه مرزی را با دقت بسیار خوبی شبیه سازی نمود. بنابراین پر واضح است که یکی از مهمترین کاربردهای این مدل، در حل مسائل مهندسی درگیر با لایه مرزی می‌باشد. مدل انتقالی یاد شده یک مدل آشفتگی سه معادله‌ای بوده که از معادلات انتقالی انرژی جنبشی آشفتگی (K)، انرژی جنبشی آرام (Kl) و گام زمانی آشفته معکوس (Inverse Turbulent Time Scale) یا همان نرخ اتلاف ویژه (ω) تشکیل شده است.

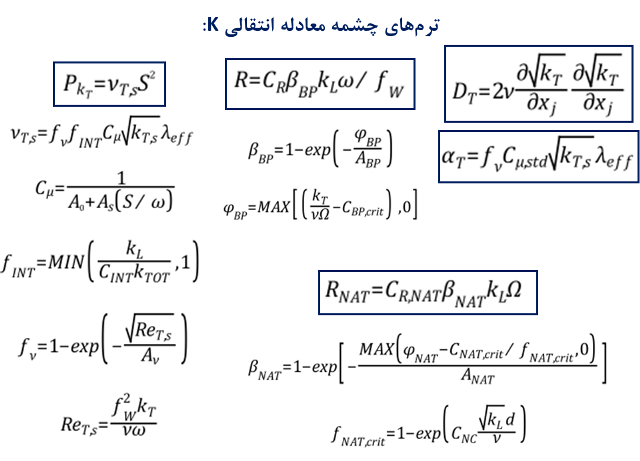
با نگاهی به معادلات فوق می‌توان به این نکته رسید که علاوه بر محاسبه انرژی جنبشی جریان آرام، در محاسبه انرژی جنبشی و لزجت آشفتگی، متغیرهای مذکور بصورت مجزا برای آشفتگی ابعاد بزرگ (Large Scale) و ابعاد کوچک (Small Scale) محاسبه می‌گردند. این مهم مدل را پیچیده، با ثابت‌های فراوان و محدود به شرایط خاصی می‌کند و دامنه کاربرد آن همانند مدل‌های خانواده K-Epsilon و K-Omega گسترده نخواهد بود. بطور کلی مهمترین ویژگی‌های این مدل عبارتند از:

از تعداد معادلات بیشتری نسبت به مدل‌های K-Epsilon و K-Omega برخوردار بوده و در نتیجه به حافظه و زمان بیشتری برای انجام محاسبات نیاز دارند.
صرفا برای جریان‌های با رینولدز پایین کاربرد دارد.
برای شبیه سازی و پیش بینی شروع و توسعه ناحیه انتقالی لایه مرزی آرام به آشفته بسیار مناسب هستند.
کاملا مناسب برای محاسبه ضرائب آئرودینامیکی وسایل پرنده با رینولدزهای پایین همانند گلایدرها و پهپادهای با سرعت پایین

آموزش تئوری و استفاده از مدل‌ K-Kl-W در نرم افزار Fluent همراه با حل یک مسئله

مدل آشفتگی چهار معادله‌ای Transition SST

مدل انتقالی SST (یا همان مدل γ-Reθ) مبتنی بر ترکیب معادلات انتقالی مدل K-Omega SST (معروف به SST-2003) و دو معادله دیگر بوده که یکی برای دل زدن یا تناوب جریان (Intermittency) و دیگری برای معیارهای تعیین نقطه شروع ناحیه انتقالی از دیدگاه عدد رینولدز ضخامت ممنتم می‌باشد. به دلیل اهمیت موضوع شبیه سازی ناحیه انتقالی، کمپانی Ansys بطور اختصاصی یک رابطه تجری را توسط لانگتری (Langtry) و منتر (Menter) و برای پوشش ناحیه انتقالی کنار گذر استاندارد (Standard Bypass Transition) همچون جریان‌های عبوری از محیط‌های کم آشفته جریان‌های آزاد، توسعه داده است. البته در نرم‌افزار Ansys Fluent آپشن بسیار کارآمدی در نظر گرفته شده تا کاربر بتواند با وارد کردن روابط اصلاحی تجربی مطلوب خود، شروع ناحیه انتقالی و عدد رینولدز ضخامت ممنتم را با دقت بهتری کنترل و پیش بینی کند.

فرمولاسیون مدل Transition SST

همانطور که گفته شد، مدل انتقالی SST از ترکیب مدل آشفتگی K-Omega-SST و دو معادله اضافی انتقالی تناوب و ضخامت لایه ممنتم بوجود آمده است. در واقع دو معادله آخر برای تصحیح مقادیر ترم‌های تولید و اتلاف انرژی جنبشی آشفتگی، K، در مدل K-Omega-SST اضافه می‌شوند. همچنین معادله انتقال مربوط به نرخ اتلاف ویژه، ω، بدون تغییر باقی می‌ماند. بطور کلی فرمولاسیون مدل انتقالی SST بصورت زیر است.

فرمولاسیون مدل آشفتگی چهار معادله‌ای گذرای SST.

در معادلات فوق:

γsep: جدایش القایی گذرا (Separation-induced Transition)
S: مقدار نرخ کرنش،
Flenght: یک رابطه تجربی کنترل کننده طول ناحیه انتقالی آرام به آشفته،
Ω: اندازه ورتیسیته،
y: فاصله از دیواره،
Reθc: عدد رینولدز بحرانی (مقدار عدد رینولدزی که در آن پدیده دل زدن یا تناوبی شدن جریان برای اولین بار در لایه رزی شروع شود. این مهم معمولا در بالادست عدد رینولدز انتقالی محاسبه شده در معادله انتقال عدد رینولدز ضخامت ممنتم، R˜eθt، اتفاق می افتد.
Reθt: عدد رینولدزی که در آن شوع ناحیه انتقالی از طریق آزمایش‌های تجربی قابل مشاهده باشد. این ترم توسط منتر (Menter) و بخاطر افزایش دقت در پیش بینی ناحیه انتقالی، اصلاح و ارائه شده است. همانطور که در روابط بالا نشان داده شده این ترم به شدت آشفتگی محلی وابسته می‌باشد. و
dU/ds: شتاب در جهت جریان است.

برای کسب اطلاعات کامل از فرمولاسیون و جزئیات این مدل روی اینجا کلیک کنید.

آموزش تئوری و استفاده از مدل‌ Transition SST در نرم افزار Fluent همراه با حل یک مسئله

شرایط مرزی مناسب برای مدل Transition SST

مقدار شار R˜eθt روی مرز دیواره صفر است. اما لازمست مقدار آن در شرایط مرزی ورودی از روابط مناسب مبتنی بر شدت آشفتگی محاسبه گردد. همچنین باید مقدار شار عمود بر دیواره برای γ، صفر و مقدار آن در مرز ورودی ، برابر با یک لحاظ گردد.

علاوه براین در نرم افزارهایی مانند Ansys Fluent، هنگام استفاده از انتقالی SST همراه با دیوراه‌های زبر، رابطه زبری تحت عنوان “Roughness Correlation” در کادر گفتگوی “Viscous Model” موجود است که با فعال کردن آن و تعیین ارتفاع هندسی (k) می‌توان اثرات هندسی تأثیر گذار روی این مدل را لحاظ نمود. قابل توجه است در فرآیند گذار آرام به آشفته، ارتفاع زبری هندسی بمراتب مهمتر از ارتفاع زبری دانه شن (Sand-Grain) معادل می‌باشد. جگونگی اندازه‌گیری ارتفاع زبری شن-دانه معادل (براساس ارتفاع زبری هندسی، شکل و توزیع المان‌های زبری) در کارهای شلیختینگ (Schlichting) و گرستن (Gersten) و همچنین کلمن (Coleman) و همکارن بطور کامل توضیح داده شده است. لازم به ذکر است مقدار هندسی مشخص شده در کادر Roughness Correlation برای تمامی مرزهای دیواره بکار گرفته می‌شود. در صورتیکه جنس و زیری سطح دیواره‌ها متفاوت باشد لازمست از UDF برای تعیین مقادیر مناسب برای هر دیواره استفاده نمود. همچنین باید توجه داشت که تابع K برای داخل فضای محاسباتی و نه روی مرز دیواره مورد استفاده قرار می‌گیرد. بنابراین این تابع باید به گونه‌ای باشد که بتواند داخل و خارج لایه مرزی را پوشش دهد.

از طرفی در تعیین شدت آشفتگی در مرزهای ورودی می‌توان مشاهده نمود که شدت آشفتگی تعیین شده در ورودی، بسته به مقدار μt/μ به سرعت مضمحل می‌شود. بنابراین شدت آشفتگی در پایین دست ورودی می‌تواند خیلی کمتر از مقدار تعیین شده برای مرز ورودی باشد. معمولا هرچه مقدار نسبت لزجت بیشتر باشد، نرخ اتلاف آشفتگی نیز کمتر می‌شود. به هر حال، اگر مقدار نسبت لزجت آشفتگی به لزجت ملکولی خیلی بزرگ فرض شود (بزرگتر از 100) مقدار ضریب اصطکاکی بطور چشمگیری با متناسب با آن در جریان آزام تفاوت پیدا می‌کند. پیشنهاد می‌شود درصورت امکان مقدار نسبت لزجت آشفتگی به ملکولی بویژه برای مسائلی نظیر آئرودینامیک خارجی، کم و بین یک تا 10 باشد.

ملاحظات شبکه‌بندی در مدل Transition SST

برای اینکه در این مدل بتوان همزمان لایه‌های مرزی آرام، گذرا و آشفته را پوشش داد لازمست شبکه تولید شده به گونه‌ای باشد تا Yplus آن تقریبا برابر با یک باشد. مقدار Yplus بین 0.1 تا 1 بهترین حالت شبکه در استفاده از این مدل آشفتگی است. اگر Yplus خیلی کوچکتر 1 باشد (کوچکتر از 0.001) باشد آنگاه شروع ناحیه‌ی گذرا بطور قابل توجهی عقب‌تر از مکان واقعی (طول لایه مرزی آرام بطور چشمگیری بیشتر از مقدار واقعی آن) پیش بینی می‌شود. برعکس اگر مقدار Yplus بسیار بزرگتر از یک (بزرگتر از 10) باشد، در اینصورت با افزایش مقدار آن نقطه شروع ناحیه گذار نیز به جلوتر از مکان واقعی آن (طول لایه مرزی آرام به نسبت مقدار Yplus کمتر از مقدار واقعی آن) محاسبه می‌شود. بطوریکه برای Yplusهای بزرگتر از 25 دیگر اثری از لایه‌های مرزی آرام و آشفته نبوده و مدل جریان را کاملا آشفته (Fully Turbulent) تشخیص می‌دهد.

کاربردها و محدودیت‌های مدل Transition SST

همانند تمامی مدل‌های آشفتگی، این مدل‌ نیز از محدودیت‌های خاص خود برخوردار است که مهمترین آن‌ها عبارتند از:

مدل گذرای SST تنها برای جریان‌های محدود به دیواره (Wall-Bounded) کاربرد دارد. همانند تمامی مدل‌های گذرای دیگر، این مدل برای استفاده در شبیه سازی ناحیه انتقالی در جریان برشی آزاد مناسب نیست. چراکه این مدل جریان برشی آزاد را به عنوان یک جریان کاملا آشفته در نظر می‌گیرد.
این مدل نمی‌تواند برای حل میدان‌های جریان همراه با سطوح متحرک نسبت به دستگاه مختصات که در آن میدان‌ سرعت محاسبه می‌گردد، بکار گرفته شود. برای چنین مسائلی لازمست از مدل انتقالی متناوب (Intermittency Transition) بجای آن استفاده نمود.
مدل مذکور برای جریان‌های با سرعت جریان آزاد غیر صفر طراحی شده است. لذا این مدل برای جریان‌های کاملا توسعه یافته در داخل لوله و یا جریان در داخل کانال‌ها که هیچ جریان آزادی در آن‌ها وجود ندارد مناسب نیست. به دلیل مشابه این مدل برای جریان‌های جت دیواره نیز مناسب نیست. برای چنین مسائلی لازمست از مدل انتقالی متناوب (Intermittency Transition) بجای آن استفاده نمود. البته باید توجه داشت که در این حالت نیز ممکن است استفاده از مدل انتقالی متناوب مستلزم انجام اصلاحاتی نیز باشد.
مدل یاد شده در ترکیب با سایر پدیده‌های فیزیکی مؤثر بر ترم‌های تولید و اتلاف معادلات مدل‌های آشفتگی (نظیر بویانسی و اثرات آشفتگی چندفازی)کالیبره نشده است بنابراین استفاده از این مدل در چنین جریان‌هایی به هیچ عنوان توصیه نمی‌گردد.

لازم به توضیح است مدل گذرای متناوب (Intermittency Transition) یک مدل یک معادله‌ای اصلاح شده بر اساس مدل γ-Reθ) می‌باشد که قابلیت کوپل شدن با مدل‌های مختلف زیر را دارد

BSL – model
SST – model
Scale-Adaptive Simulation with BSL or SST
Detached Eddy Simulation with BSL or SST
Shielded Detached Eddy Simulation (SDES) with BSL or SST
Stress-Blended Eddy Simulation (SBES) with BSL or SST

بطور خلاصه بهترین عملکرد این مدل در محاسبه دقیق ضریب درگ اصطکاکی و شبیه سازی دقیق لایه‌های مرزی همراه با پوشش ناحیه گذرا برای آئرودینامیک خارجی در سرعت‌ها و رینولدزهای پایین می‌باشد.

ادامه دارد…

بازگشت

مطالب مرتبط