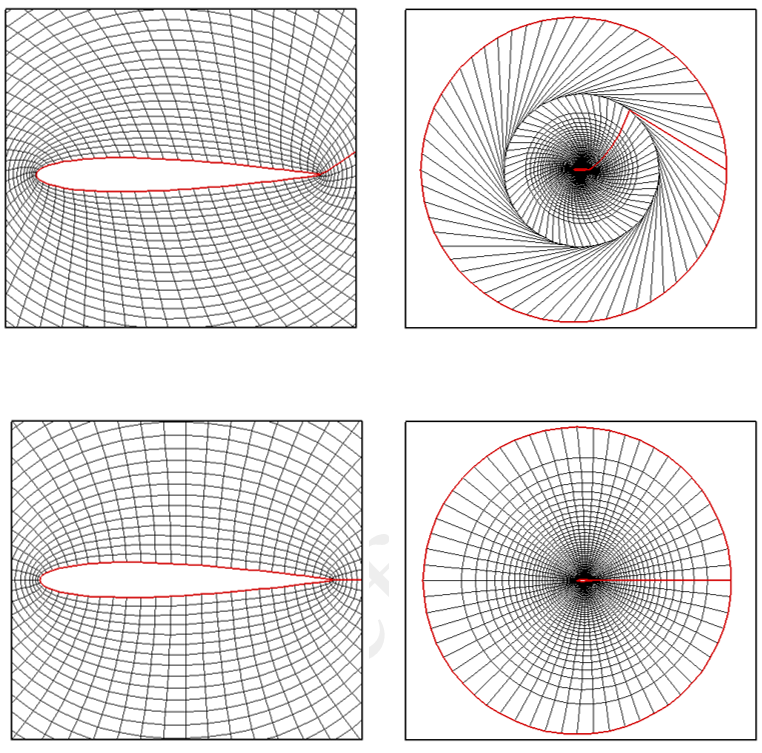
شبکه (مش) بندی باسازمان ایرفویل NACA0012 با استفاده از روشهای نگاشتی (Mapped)
NACA0012 Airfoil Mapped Structured Grid Generation
به عنوان یک مثال شبکه (مش) بندی باسازمان ایرفویل NACA0012 با استفاده از روشهای نگاشتی (Mapped) تشریح شده است. بگذارید از ابتدا شروع کنیم. برای اینکه حول ایرفویل یک شبکه تولید کنیم اولا لازمست مرزهای خارجی و داخلی (هندسه ایرفویل) را بدانیم. مرز خارجی معمولا یک دایره با فاصله مشخصی از ایرفویل در نظر گرفته میشود. ثانیا باید توزیع نقاط مناسبی روی ایرفویل داشته باشیم تا شبکه تولید شده از کیفیت مناسبی برخوردار باشد. با تعیین مرزهای داخلی و خارجی و همچنین توزیع مناسب نقاط شبکه روی آنها فرآیند شبکه بندی دامنه محاسباتی انجام میشود.
تعیین هندسه ایرفویل و مرز خارجی
به طور کلی مشخصات هندسی ایرفویلهای چهار رقمی خانواده NACA با استفاده از معادلات (19) و (20) که براساس پارامترهای شکل (1) تعریف شده، مشخص میشود.

قابل توجه است در معادله (99) هندسه خط کوژ (camber line) و در معادله (100) چگونگی توزیع ضخامت ایرفویل تعیین میشود. در معادلات فوق yc، yt و x پارامترهای بدون بعد شده نسبت به وتر(chord line) ایرفویل هستند. همچنین، τ بیشترین مقدار ضخامت، بیشترین مقدار کوژ و مکانی که کوژ بیشترین مقدار را دارد تعریف میشوند. نکتهای که در معادلات فوق باید مورد توجه قرار گیرد آن است که در لبه فرار ضخامت ایرفویل صفر نیست. لذا، میتوان به صورت دستی در x=1 مقدار yt را صفر قرار داد. همچنین، در این معادلات مرکز مختصات در نوک لبه حمله (نه در مرکز دایره) قرار دارد.
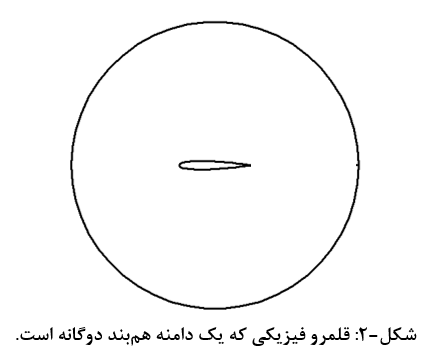
دامنه هندسی تعیین شده یک دایره به قطر 5 (البته در عمل لازمست این کمیت خیلی بیشتر از این قرار گیرد تا بتوان شرط جریان را روی مرز خارجی با دقت مناسب استفاده نمود) و مرکز منطبق بر وسط وتر ایرفویل (شکل-2) است. هدف تولید شبکه باسازمان با استفاده از روشهای جبری و دیفرانسیلی بیضوی (حل معادله لاپلاس) در قلمرو فیزیکی یاد شده است که در ادامه بطور کامل تشریح شده است.
توزیع کسینوسی نقاط روی ایرفویل و مرز بیرونی
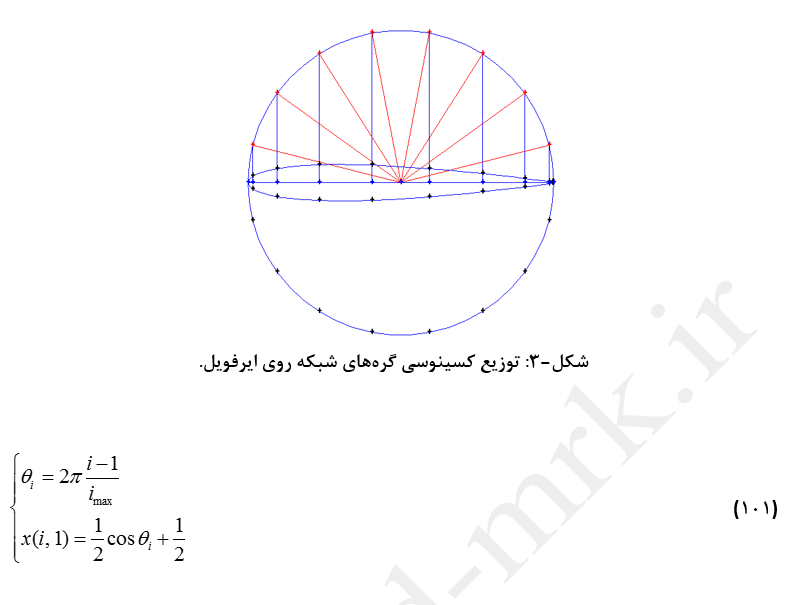
قبل از پرداختن به هر روش باید توزیع نقاط (گرههای محاسباتی) روی ایرفویل مشخص گردد. یکی از راههای تولید نقاط محاسباتی روی ایرفویل توزیع کسینوسی است. اگر شماره گرههای محاسباتی در امتداد سطح ایرفویل و شماره گرهمحاسباتی در راستای شعاع دامنه محاسباتی باشد، آنگاه توزیع گرههای محاسباتی با استفاده از توزیع کسینوسی طبق معادله (101) انجام میشود (شکل3). لازم به ذکر است برای درک بهتر توزیع کسینوسی روی دایره ای هم اندازه با ایرفویل نیز در این شکل نشان داده شده است.
شبکه (مش) بندی باسازمان ایرفویل: روشهای جبری
روشهای جبری TFI تولید شبکه امکان کنترل مستقیم روی توزیع نقاط شبکه را فراهم میکند. برخی سیستمهای جبری باعث انتشار ناپیوستگی شیب مرز به داخل ناحیه میشود. این موضوع از خاصیتهای ذاتی چنین روشی، مانند آنچه در سیستمهای هذلولی موجود بوده، نیست. استفاده از درونیابیهای موضعی در روشهای بویژه جبری، مانند روش چندصفحهای (Multi-Surface) ، میتواند از انتشار این ناپیوستگی به درون میدان جلوگیری کند.
بطور کلی، تولید شبکه با روشهای جبری (توزیع نقاط) درواقع کاربردی از درونیابیهای ریاضی میباشد. این روشها درعین حالی که برای تولید شبکه ساده بوده و نیز کنترل شبکه را به راحتی میسر میسازد، اما نیازمند دقت ویژه در نوشتن برنامه و همچنین چگونگی استفاده از آن میباشد. جزئیات کامل تولید شبکه باسازمان با استفاده از سیستم معادلات جبری، در اینجا ارائه شده است. مهمترین روشهای توزیع نقاط در تولید شبکه جبری عبارتست از توزیع نمایی، تانژانت هایپربولیک و سینوس هایپربولیک میباشد که در این مثال نیز مورد بررسی قرار گرفته است.
تولید شبکه جبری با استفاده از توزیع نمایی
پس از تعیین نقاط روی مرزهای داخلی و خارجی با استفاده از توزیع کسینوسی، یکی از راههای گسستهسازی خطوط بین نقاط مرزهای داخلی و خارجی، روش میانیابی خارج از اعداد محدود (TFI) است. در این روش از رابطه نمایی انبساطی (معادله 102) استفاده میشود.
در رابطه فوق –r بوسیله فاصله بین دو گره مرز داخلی و گره داخل دامنه محاسباتی بدون بعد شده (شکل4) و نیز بیشترین تعداد المانها در راستای شعاع دامنه محاسباتی میباشد. σ پارامتر تراکمسازی شبکه است. تجربه نشان داده که بهترین مقدار برای این پارامتر مقادیر بین 1 تا 10 میباشد که در آن شبکه از کیفیت مطلوبی از لحاظ تغییر مساحت المانهای مجاور برخوردار باشد. از آنجائیکه –r یک پارامتر بدون بعد است، در طی فرآیند محاسبات باید در li (معادله 103) ضرب شود.

بنابراین، مختصات نقطه A نشان داده شده در شکل (4) از رابطه (104) محاسبه میشود (زیر نویس i در روابط زیر حذف شده است). با توجه به معادله (105) معادله (104) را میتوان به صورت رابطه (106) بازنویسی کرد.

جزئیات شبکه تولید شده (20*40) با این روش در شکلهای (5) تا (9) نشان داده شده است.
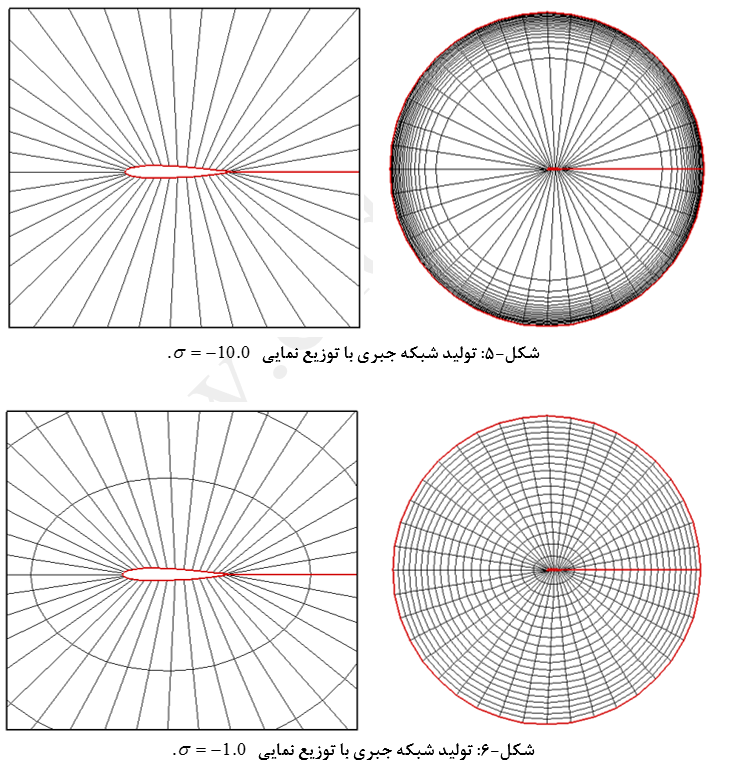
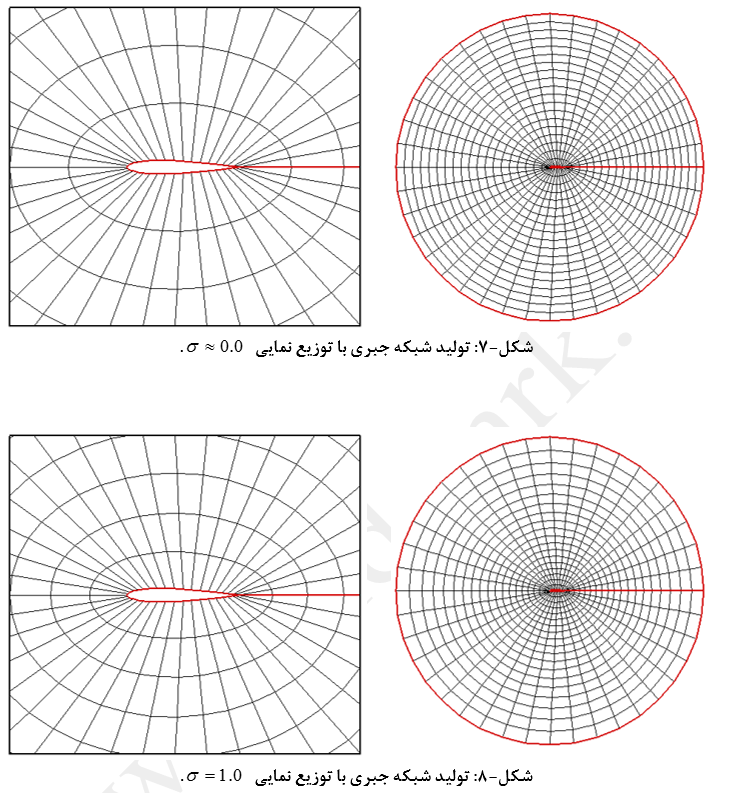
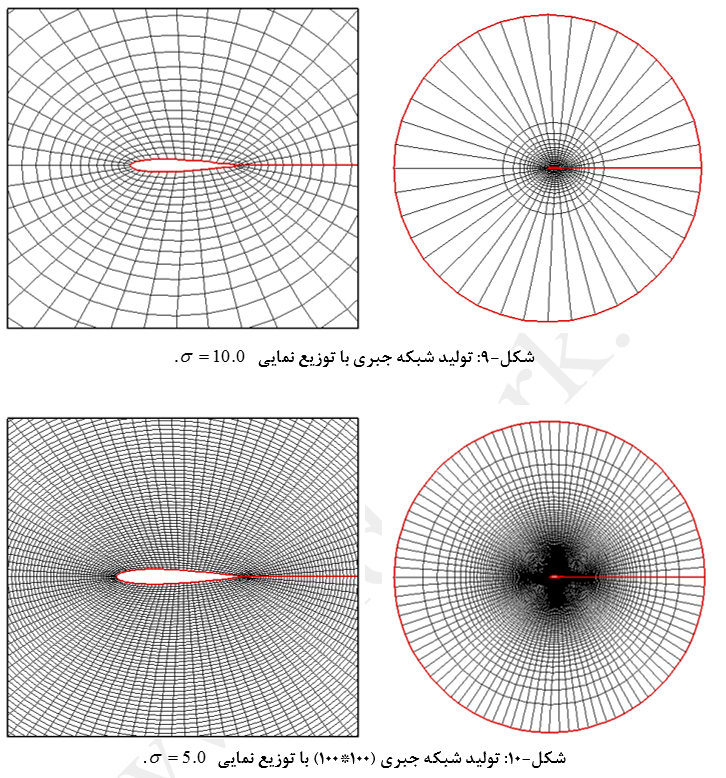
با توجه به معادله (102) مقدار σ=0 در واقع یک نقطه تکین می باشد. متراکم سازی نقاط با استفاده از روش یاد شده تنها از یک طرف امکان پذیر است. استفاده از این روش برای پوشش دادن لایه مرزی مناسب نیست چرا که لازمست در چنین حالتهایی مقدار σ خیلی بزرگ در نظر گرفته شود (بزرگتر از 100) که این مسئله باعث پرش ناگهانی در اندازه مساحتهای المانهای همسایه خواهد شد (شکل-10) که نوسانی شدن باقیماندهها و نرخ همگرایی بسیار پایین را به دنبال خواهد داشت.
تولید شبکه جبری با استفاده از توزیع تانژانت هایپربولیک
روش تانژانت هایپربولیک نیز یکی دیگر از روشهای توزیع غیر یکنواخت نقاط میباشد. برخلاف روش قبل این روش توانایی تراکمسازی دو طرفه نقاط را نیز دارد. رابطه استفاده شده برای توزیع نقاط با روش مذکور طبق معادله (107) است.
در رابطه (108)، δ با استفاده از معادله (110) و با روش سعی و خطای نیوتن رافسون (111) تعیین می گردد. ΔS1 و ΔS2 نیز نسبت فواصل ابتدایی و انتهایی خط میباشند. پارامتر B در معادله (30) نیز طبق رابطه (112) تعریف میشود.

جزئیات تولید شبکه جبری 20*40 و 100*100با این روش در شکلهای (11) تا (16) نشان داده شده است.
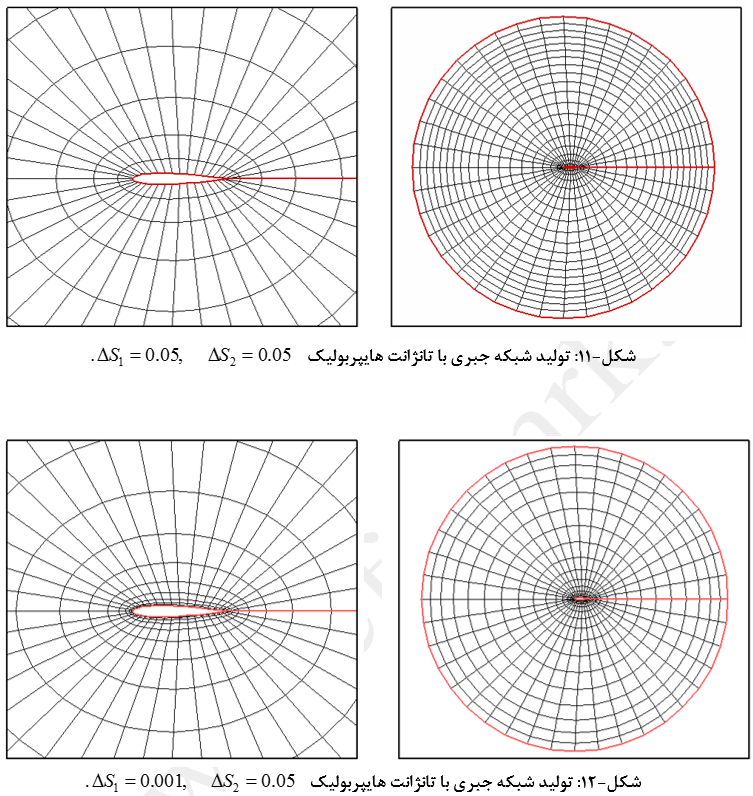
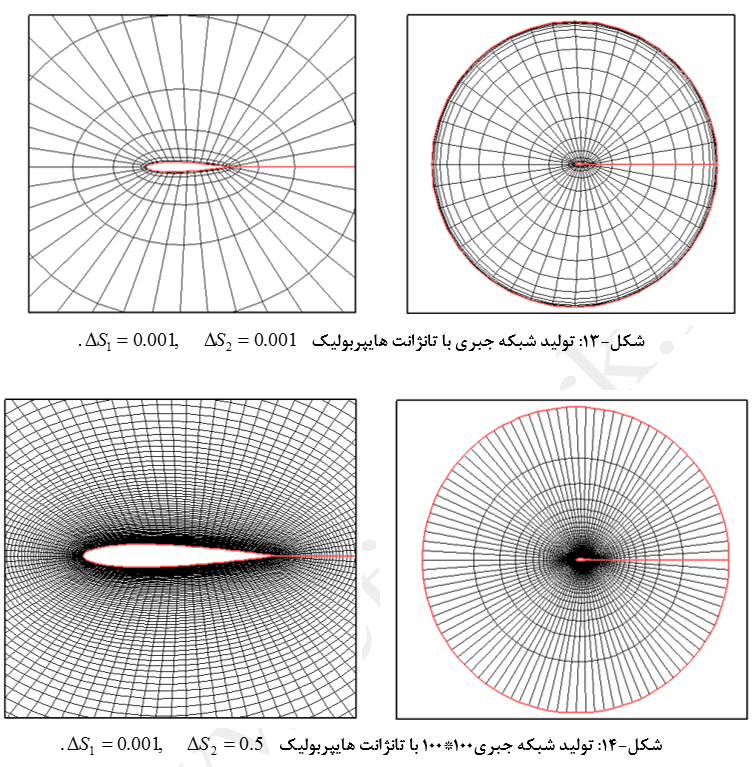
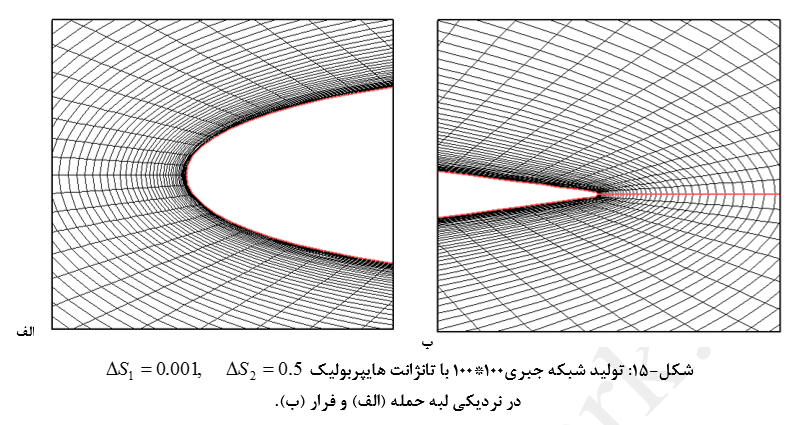
شبکه بندی با روش تانژانت هایپربولیک برای حالتهای مختلف نشان داده است که این در روش کنترل شبکه لایه مرزی بسیار بهتر از توزیع نقاط نمایی میباشد. از طرفی در این روش رشد اندازه المانها نسبت به روش نمایی نیز کمتر است که این موضوع نیز یکی دیگر از مزایای توزع تانژانتی نقاط بشمار میرود. مهمترین نقطه ضعف این روش محدودیت در مقدار بازه قابل قبول برای ΔS1 و ΔS2 میباشد.
تولید شبکه جبری با استفاده از توزیع سینوس هایپربولیک
کلیات توزیع نقاط به روش سینوس هایپربولیک همانند روش تانژانت هایپربولیک است. در این روش تابع توزیع نقاط روی دامنه محاسباتی به صورت معادله (113) تعریف میشود.

سایر تعریفها و روابط همانند روش تانژانت هایپربولیک میباشد که در اینجا از تکرار آن خودداری شده است. جزئیات تولید شبکه جبری 20*40 با این روش در شکلهای (16) تا (19) نشان داده شده است. شبکههای نشان داده شده در شکل (20) نیز بیانگر تفاوت تولید شبکه به روشهای تانژانت هایپربولیک و سینوس هایپربولیک میباشد.
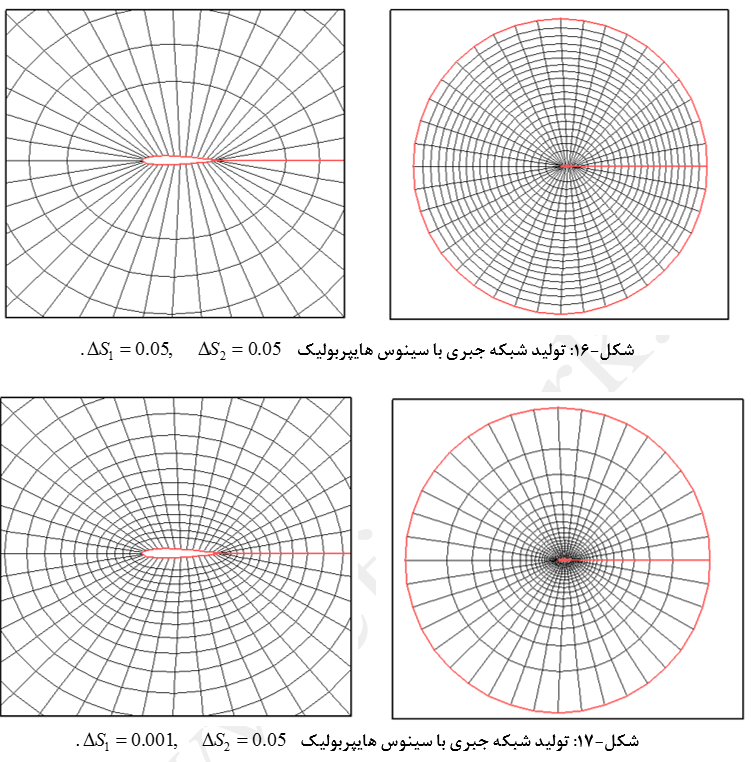
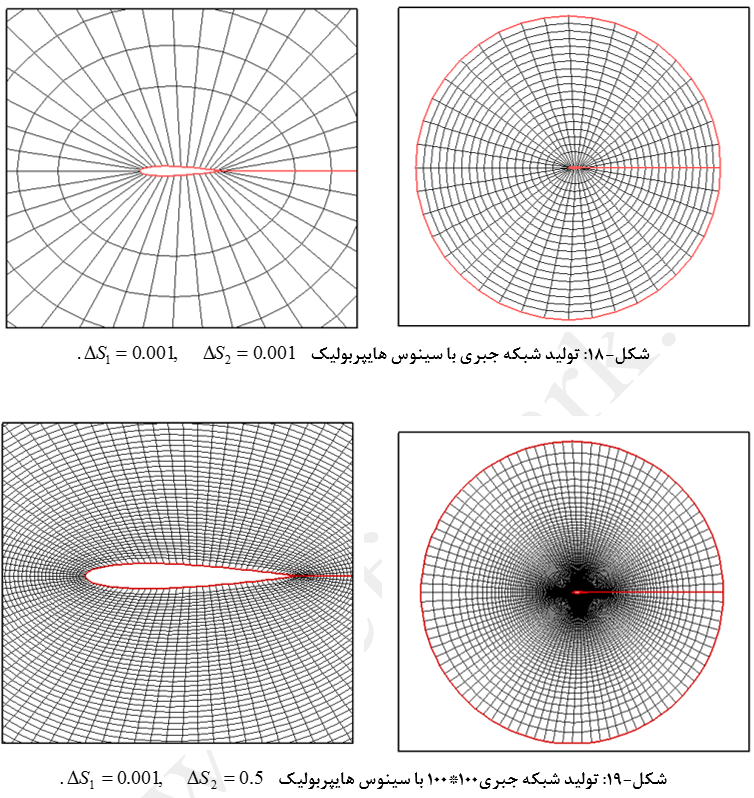
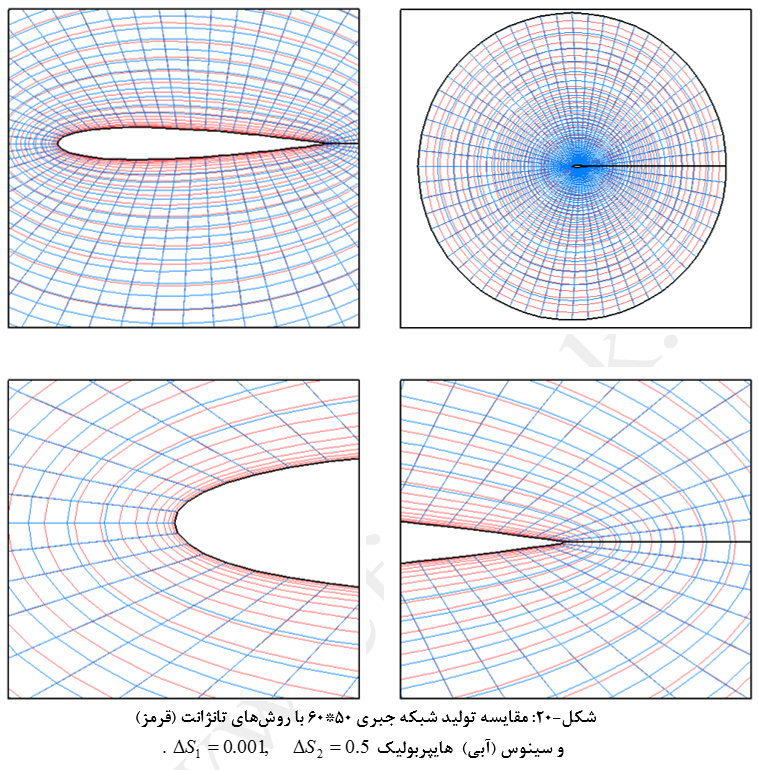
مهمترین نکته در شبکهبندی به روش سینوس هایپربولیک اینست در صورتیکه ΔS1 و ΔS2 با هم برابر باشند شبکه تولید شده مستقل از مقدار آنها خواهد بود (شکلهای 17 و 19). از طرفی شدت متراکمسازی شبکه در دو سر خطوط (هم ابتدا و هم انتها) در این روش نسبت به روش تانژانت هایپربولیک بسیار کمتر است (شکل 20). در روش مذکور رشد المانها به مراتب از دو روش قبلی کمتر است.
شبکه (مش) بندی باسازمان ایرفویل: روشهای دیفرانسیلی بیضوی
استفاده از روش تولید شبکه بیضوی برای مرزهای مشخص بهترین گزینه است. در این روش دستگاه معادلات بصورت معادلات دیفرانسیل جزئی بیضوی (معادلات لاپلاس یا پوآسون) استفاده میشود. از حل این دستگاه معادلات، مختصات نقاط شبکه به صورت نقاط شبکه در فضای فیزیکی به دست میآید. برای حل معادلات دیفرانسیل جزئی بیضوی از روشهای تکراری مانند گوس-سایدل و غیره استفاده میشود.
تولید شبکه با استفاده از معادله لاپلاس
معادله لاپلاس اساس استفاده از معادلات دیفرانسیل جزئی بیضوی در تولید شبکه است. مختصات x و y نقاط شبکه در فضای فیزیکی است. بنابراین، در یک فضای بسته، ابتدا با استفاده از یکی از روشهای جبری، توزیع گرهها روی مرزها مشخص گشته و سپس مختصات نهایی نقاط شبکه از حل دستگاه معادلات بیضوی به دست میآید. برای درک بهتر، دستگاه معادلات لاپلاس (116 و 117) را در نظر بگیرید.
که در آن، ξ و η مختصات در قلمرو محاسباتی است. معادلات (116) و (117) را میتوان با یکی از روشهای تشریح شده در اینجا حل کرد. برای تبدیل معادلات دیفرانسیل جزئی بیضوی، متغیرهای وابسته و مستقل باید جا به جا شوند. در نتیجه معادلات بیضوی (116) و (117) به صورت زیر روابط (118) و (119) نوشته میشوند.

دستگاه معادلات بیضوی (118) و (119) در فضای محاسباتی (ξ, η) حل میشود تا مختصات نقاط شبکه در فضای فیزیکی (x, y) به دست آید. باید دانست که این معادلات غیر خطی هستند. بنابراین، باید از یک روش خطیسازی استفاده نمود. برای سادگی از روش تأخیری برای ضرائب استفاده میشود. به عبارت دیگر ضرائب a، b و c از نتایج تکرار قبل محاسبه میشود.
برای بررسی چند روش حل تکراری، معادلات تفاضل محدود را با تقریب زدن معادلات دیفرانسیل جزئی به کمک عبارتهای تفاضل محدود مرکزی مرتبه دوم به دست میآوریم. بنابراین، از معادله (118) به معادله (123) میرسیم. از روش تکراری گوس-سایدل، معادله (123) به صورت رابطه (124) بازنویسی میشود. با مرتب کردن این رابطه به معادله نهایی (125) میرسیم. به طریق مشابه برای معادله (119) نیز رابطه (126) استخراج میشود.

شبکه (مش) بندی باسازمان ایرفویل
برای شروع حل باید توزیع اولیه مختصات x و y نقاط شبکه در فضای فیزیکی داده شود. همان گونه که قبلاً اشاره شد، میتوان از یک شبکه جبری بعنوان حدس اولیه برای تولید شبکه باسازمان با روش دیفرانسیل جزئی استفاده کرد. ضرائب a، b و c که در معادلات (125) و (126) ظاهر میشوند، با استفاده از تقریب تفاضل محدود معادلات (120) تا (122) به دست میآیند. در این معادلات، مقادیر x ، y با توزیع اولیه این مقادیر برای تکرار اول تأمین میشوند و به دنبال آن از روی مقادیر تکرار قبلی محاسبه میشوند، به این معنی که محاسبه ضرائب همواره یک گام عقبتر است. روش تکرار آنقدر ادامه مییابد تا معیار خاصی ارضا شود. بر همین اساس، خطای کلی به صورت زیر به دست میآید:

در معادلات فوق k مرحله تکرار را نشان میدهد. معیار همگرایی به صورت است که در آن مقدار مشخصی برای تعریف میشود.
البته، برای حل دستگاه معادلات (125) و (126) از روشهای تکرار دیگر نیز میتوان استفاده کرد. بعنوان مثال، فرمولاسیون روش تکرار گوس-سایدل خط به خط برای این دستگاههای معادلات در قالب معادلات (127) و (128) نوشته میشود. همچنین، برای روش تکرار خطی خلاصی روابط (129) و (130) حاکم هستند.

شبکه (مش) بندی باسازمان ایرفویل : معادله لاپلاس
لازمست توزیع نقاط شبکه روی مرزها در فضای فیزیکی و همچنین توزیع اولیه نقاط داخلی معلوم باشد. محاسبه مقادیر جدید x1,j و y1,j بعد از هر مرحله تکرار ضروری است. مقادیر xIM,j و yIM,j نیاز به محاسبه ندارد، زیرا خطوط i=1 و i=IM برهم منطبق هستند. بنابراین، x1,j= xIM,j و y1,j= yIM,j. با استفاده از روش گوس-سایدل، x1,j و y1,j با استفاده از روابط (131) و (132) محاسبه میشوند.
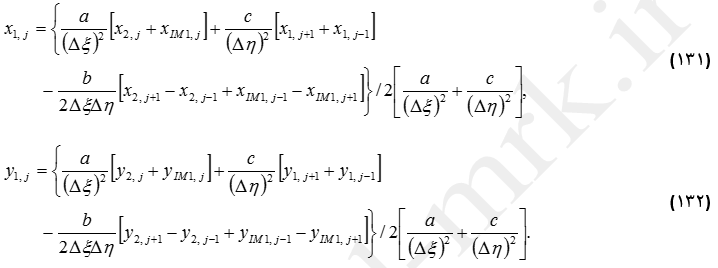
که در آن، IM1=IM-1 است. بعد از هر تکرار از این معادلات برای محاسبه موقعیت نقاط شبکه در امتداد خط برش استفاده میشود. باید دانست که اگر نقاط شبکه در امتداد خط برش ثابت در نظر گرفته شوند، اعوجاج شدیدی در آن امتداد ایجاد میشود که نامطلوب است.
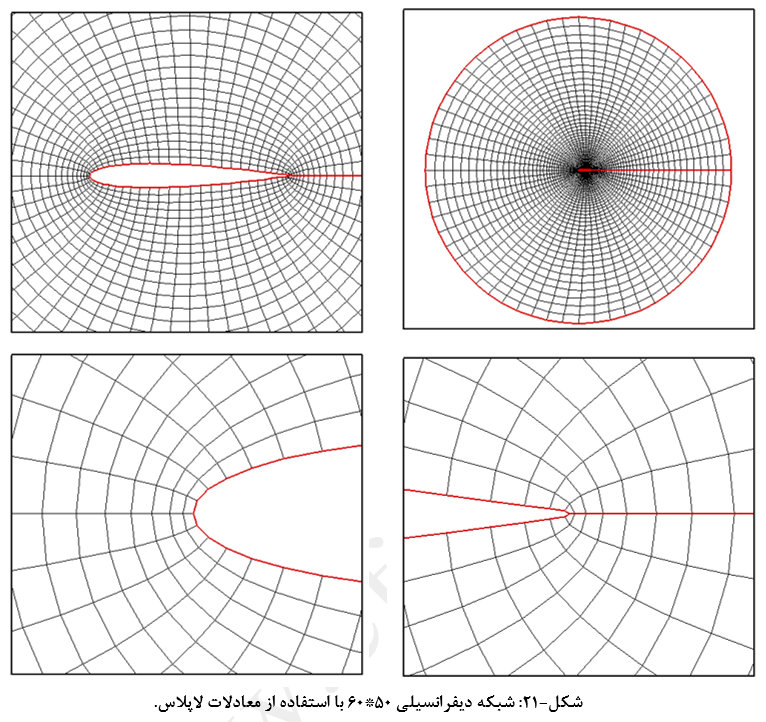
لازم به ذکر است که روش استفاده شده برای حل معادله لاپلاس روش گوس-سایدل نقطه به نقطه میباشد. بدیهی است که شبکه نهایی مستقل از روش حل عددی می باشد اما، نکته قابل توجه در تولید در روش مذکور اینست که شبکه نهایی تولید شده مستقل از حدس اولیه (شبکه جبری اولیه تولید شده) نیز می باشد. برای نمونه شبکه تولید شده به روشهای جبری بعنوان حدس اولیه برای شبکه بندی با استفاده از معادلات لاپلاس مورد استفاده قرار گرفت. شکلهای متفاوت شبکه برای حدس اولیه تنها در تعداد تکرار همگرایی موثر است. برای حدس اولیه به روش تانژانت هایپربولیک به 1838 تکرار و برای سینوس هایپربولیک به 1823 تکرار نیاز است تا باقیمانده تکرار کمتر از 00001/0 شود. با توجه به مطالب بیان شده، شبکه تولید شده برای این مثال با استفاده از روش دیفرانسیلی بیضوی (معادلات لاپلاس) یکتا بوده که در شکل (21) نشان داده شده است.
تولید شبکه با استفاده از معادله پوآسون
معادلات دیفرانسیل جزئی بیضوی لاپلاسی (116) و (117) دارای هیچگونه امکان کنترل شبکه (جهت ریز یا درشت کردن آن در قسمتهای خاص)نیستند. از طرفی، موقعیت نقاط روی بدنه جسم و روی مرز خارجی به عنوان ورودی مطرح است. برای کنترل نقاط داخلی شبکه میتوان از معادله پوآسون استفاده نمود. مبنای این امر همان است که در ابتدای این بخش به آن اشاره شده و مجدداً در این قسمت بطور خلاصه مورد بررسی قرار میگیرد. برای مثال، انتقال حرارت هدایتی در حالت دو بعدی را در نظر بگیرید. با تغییر مکان و قدرت چشمه حرارتی، خطوط هم دما تغییر میکند. این منطق به روش تولید شبکه با معادلات دیفرانسیل بیضوی تعمیم داده میشود. از این رو، یک عبارت چشمه به سمت راست معادلات (116) و (117) اضافه میشود. معادلات پوآسون حاصل به صورت روابط (133) و (134) خواهد بود.
از آنجا که این معادلات در یک قلمروی مستطیلی با فواصل شبکه مساوی حل میشوند، تبدیل معادلات و شرائط مرزی ضروری است. برای اینکار از معادلات (135) و (136) میباشد.
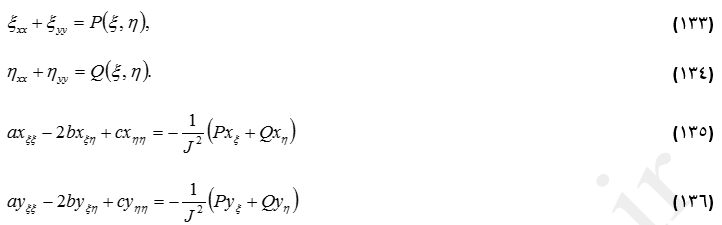
اگر P و Q معلوم باشند، این معادلات بیضوی با هر روش تکرار قابل حل خواهد بود. توابع P و Q بسته به نوع نیاز انتخاب میشود. نیاز ممکن است ایجاد تراکم در یک جای خاص یا تعامد خطوط شبکه بر سطوح جسم باشد. البته برای این مثال مقادیر ثابتی برای P و Q در نظر گرفته شده که در در شکلهای (22) تا (30) نشان داده شده است.
شبکه (مش) بندی باسازمان ایرفویل
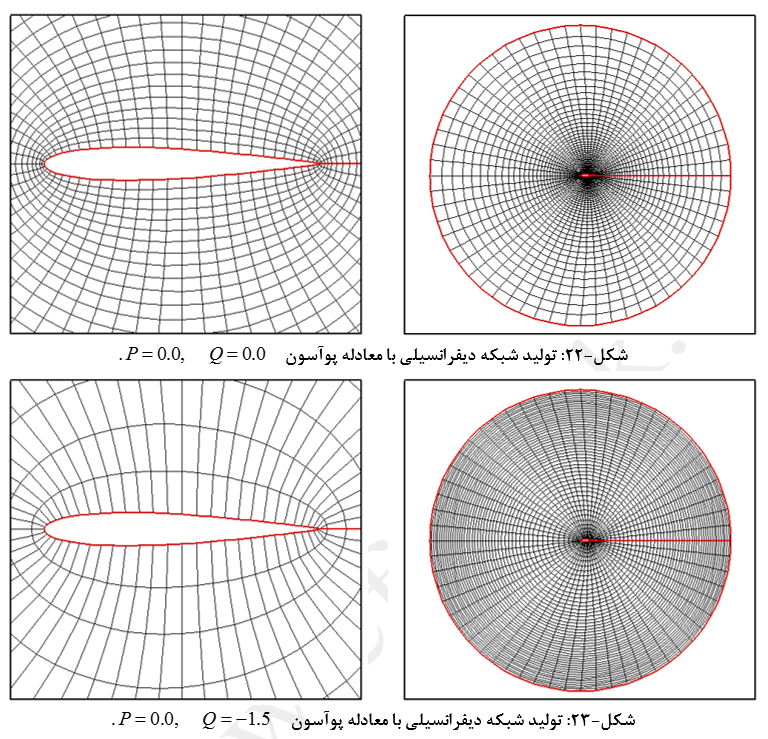
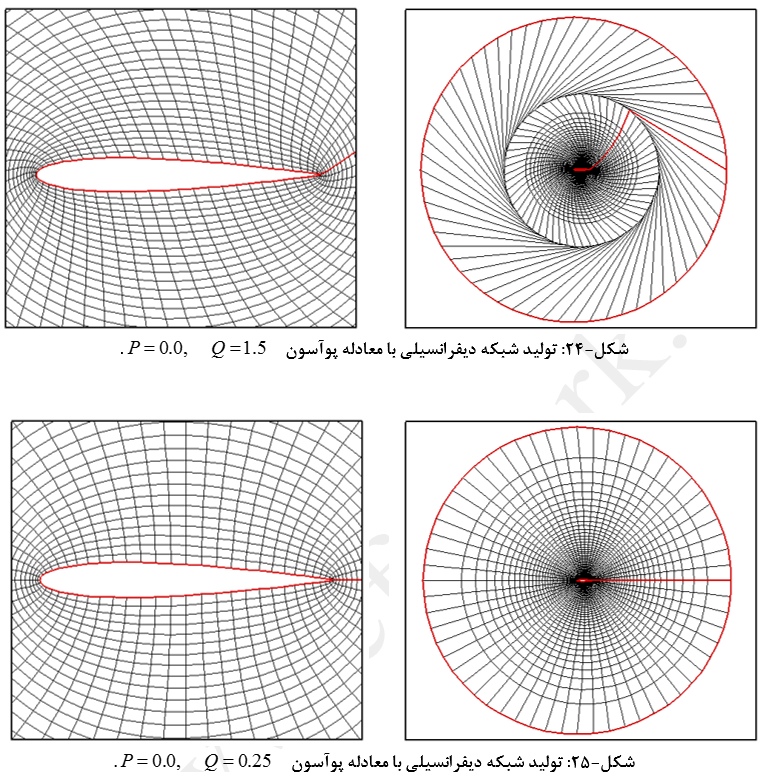
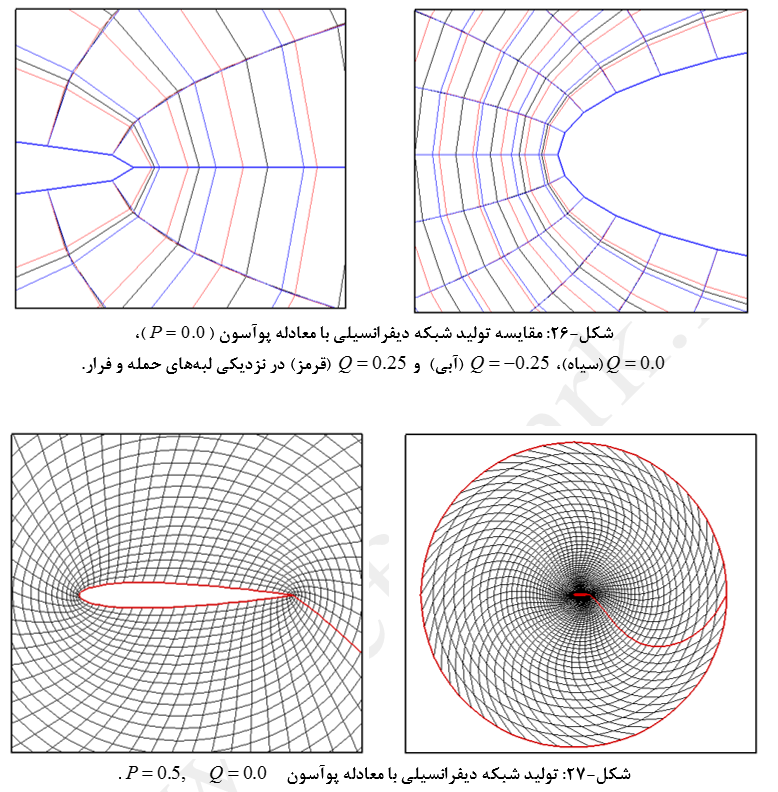
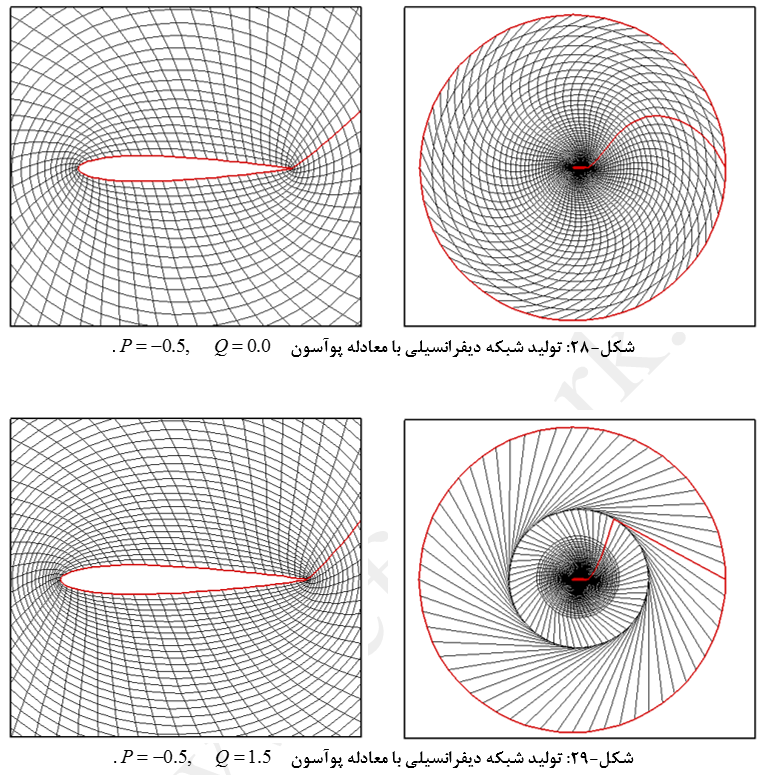
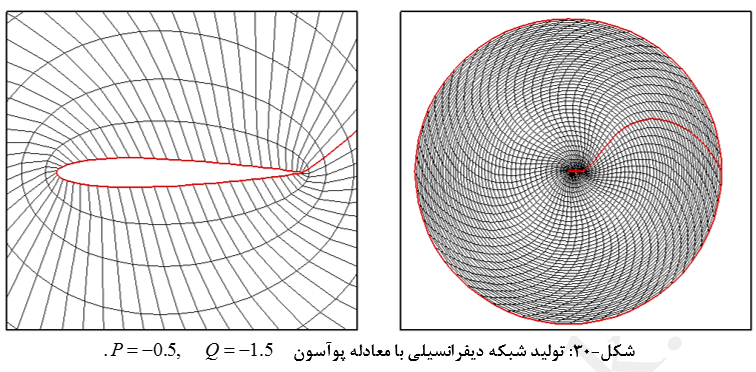
با توجه به حالتهای مختلف شبکه بندی با استفاده از معادلات پوآسون میتوان نتیجه گرفت:
- پارامترهای P و Q به ترتیب بر تغییر شکل شبکه در جهت زاویه ای و شعاعی تأثیر گذار هستند.
- دامنه تغییرات پارامترهای فوق بصورت اعداد ثابت بسیار محدود است.
- تغییرات P و Q بصورت اعداد ثابت در کیفیت شبکه تولید شده و همچنین کنترل توزیع نقاط تا حدود بسیار زیادی ناکارآمد است و لازمست از توابع برای تعریف آنها بهره جست.
- پارامترهای P و Q بر تعامد المانهای شبکه نیز به شدت تأثیر گذارند.