تئوری مدل برخورد و ادغام قطرات
Collision and Droplet Coalescence Model Theory
تئوری مدل برخورد و ادغام قطرات اساسا برای پیشگویی احتمال برخورد قطرات و اتفاقات پسا-برخورد توسعه یافته است. هنگامیکه مدلسازی رصد قطرات را هم شامل میشود، میتوانید از روشی مناسب برای تخمین تعداد برخورد قطرات و نتایج آنها استفاده کنید. مشکل شبیهسازی برخورد قطرات در این است که برای N قطره، هر یک از قطرات احتمال دارد با یکی از N-1 قطره باقیمانده برخورد کند. بنابراین، تعداد امکان برخورد نهایی کل قطرات تقریبا 0.5N2 میباشد. ضریب 0.5 بخاطر اینست که برخورد قطره A به B و بر عکس آن برخورد قطره B به قطره A تنها یک بار در نظر گرفته میشود. این تقارن تعداد حلتهای احتمالی برخورد را به نصف کاهش میدهد.
نکته مهم آن است که الگوریتم برخورد باید 0.5N2برخورد احتمالی بین قطرات را در هر گام زمانی محاسبه کند. از آنجائیکه پدیده پاشش اسپری میلیونها قطره را در خود جای میدهد، لذا هزینه محاسباتی تحلیل برخورد قطرهها بسیار زیاد است. این چالش انگیزه مناسبی را برای استفاده از مفهوم پارسل (Parcel) فراهم میکند. پارسلها نمایندههای آماری چندین قطره مجزا هستند. در واقع یک پارسل مجموعهای از تعدادی قطره است. به عنوان مثال اگر هر پارسل یک نماینده محاسباتی برای 1000 قطره باشد، آنگاه هزینه محاسبات با ضریب 106 کاهش مییابد. از آنجایی که هزینه محاسبات برخورد همچنان N2 است، بنابراین کاهش هزینهها با استفاده از مفهوم پارسل بسیار چشمگیر خواهد بود. با این حال محاسبه تقاطع احتمالی بسیاری از مسیرهای پارسلها همچنان پرهزینه باقی میماند.
الگوریتم او-رورک (O’Rourke) به طور مؤثری هزینه محاسبات برخورد قطرات در پاشش را کاهش میدهد [1]. روش او-رورک به جای استفاده از پارامترهای هندسی برای بررسی امکان برخرود مسیر پارسلها، از یک تخمین تصادفی برای برخوردها استفاده میکند. همچنین این متد فرض میکند که تنها زمانی دو پارسل ممکن است با هم برخورد کنند که در یک سلول فاز پیوسته قرار داشته باشند. این دو فرض تنها در زمانی صادق است که اندازه المان فاز پیوسته در مقایسه با اندازه پاشش کوچک باشد. تحت این شرایط، روش او-رورک شانس برخورد را با استفاده از دقت مرتبه دوم تحلیل میکند. مفهوم پارسلها همراه با الگوریتم او-رورک محاسبات برخورد قطرات در جریانهای همراه با پاشش را امکانپذیر میسازد.
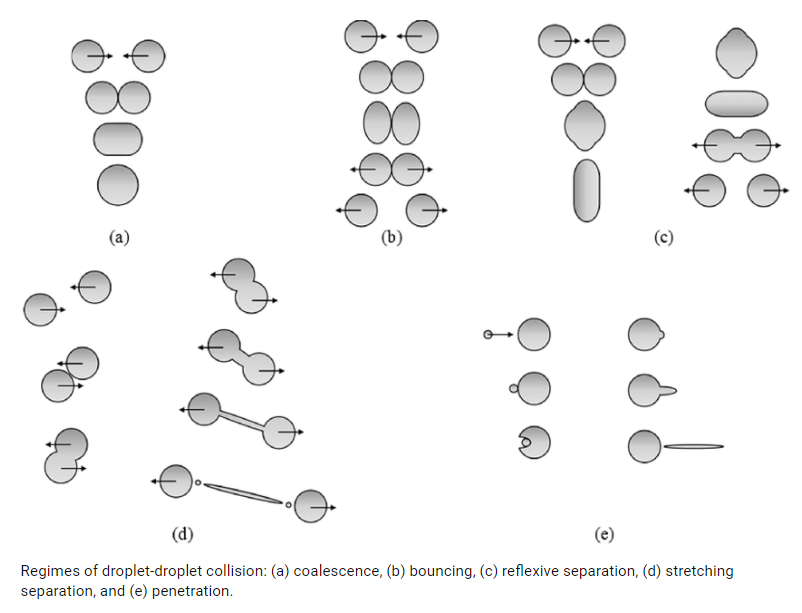
با قطعی شدن تصمیم برخورد بین پارسلها، الگوریتم او-رورک نوع برخورد را مشخص میکند. نتیجه برخورد تنها به ادغام (Coalescence) و پرش (Bouncing) ختم میشود. احتمال هر نتیجهی برخورد براساس عدد وبر برخوردی (collisional Weber number)، Wec، تعریف شده در معادله (459)، محاسبه شده و با مشاهدات تجربی تطبیق داده میشود. در این رابطه Urel سرعت نسبی بین دو پارسل و –D متوسط قطر محاسباتی دو پارسل است. وضعیت دو پارسل برخورد کننده براساس پیامدهای برخورد تصحیح میشود.

کاربردها و محدودیتهای مدل برخورد و ادغام قطرات
مدل برخورد فرض میکند که فرکانس برخوردها بسیار کمتر از گام زمانی ذره است. اگر گام زمانی ذره بیش از اندازه بزرگ باشد، آنگاه ممکن است نتایج برخورد به گام زمانی وابسته شود. بنابراین، لازمست که مقیاس طول ذرات را براساس این موضوع تنظیم کنید. به علاوه، این مدل برای برخوردها در اعداد وبر پایین که در آن برخوردها به ادغام و پرش منجر میشوند، بیشترین کاربرد را دارد. در اعداد وبر بالای 100 نتیجه برخورد ممکن است به تخریب و شکست قطرات همراه باشد.
گاهی اوقات مدل برخورد میتواند موجب بروز نتایج وابسته به شبکه برای شبیهسازی اسپری بشود. این همه نتیجه این فرض است که قطرات تنها در یک سلول میتوانند با هم برخورد داشته باشند. این موارد زمانیکه نقطه تزریق روی یک گره محاسباتی شبکه واقع شده باشد قابل مشاهده است. ادغام قطرات موجب دور شدن پاشش از مرزهای سلولی میشود. در مسائل دو بعدی میتوان با استفاده از شبکه ریزتر و قطرات محاسباتی بیشتر خطای ناشی از این اثرات را کاهش داد. در مسائل سه بعدی بهترین نتایج زمانی به دست میآید که پاشش در مرکز یک شبکه قطبی مدلسازی شود.
اگر از مدل برخورد در شبیهسازی جریان ناپایا استفاده شود لازمست محاسبات مربوط به DPM برای هر گام زمانی انجام شود.
تئوری مدل برخورد و ادغام قطرات
همانطور که در بالا بیان شد، الگوریتم او-رورک فرض میکند که دو قطره تنها زمانی ممکن است با یکدیگر برخورد کنند که در یک سلول فاز پیوسته قرار داشته باشند. این فرض ممکن است از برخورد قطرات بسیار نزدیک به هم اما در سلولهای جداگانه جلوگیری کند. البته این خطا با برخورد قطرات دورتر از هم اما واقع در یک سلول تا حدودی کاهش مییابد. این مدل از دقت مرتبه دوم مکانی استفاده میکند.
احتمال برخورد
محاسبات مربوط به احتمال برخورد دو قطره از دید قطره بزرگتر که جمع کننده یا کالکتور (Collector) نامیده شده و با شماره 1 مشخص میشود، صورت میگیرد. قطره کوچکتر نیز با عدد 2 نامگذاری میشود. محاسبات در قاب مرجع (Reference Frame) بزرگتر انجام میشود به طوریکه سرعت قطره کالکتور در آن صفر است. در این محاسبات تنها فاصله بین قطرات 1 و 2 اهمیت دارد. اگر قطره کوچکتر در مسیر برخورد با قطره بزرگتر باشد، آنگاه مرکز دو قطره در فاصله r1+r2 از یکدیگر عبور خواهد کرد.
به عبارت بهتر اگر مرکز قطره کوچکتر از داخل یک دایره مسطح به مرکز واقع در محدوده قطره کالکتر و با مساحت π(r1+r2)2 عمود بر مسیر قطره کوچکتر عبور کند، برخورد اتفاق میافتد. از این دایره برای محاسبه حجم برخورد نیز استفاده میشود که مقدار آن برابر است با حاصل ضرب مساحت دایره با فاصله طی شده توسط قطره کوچکتر در یک گام زمانی و در نتیجه مقدار آن برابر با π(r1+r2)2VrelΔt خواهد بود.
الگوریتم او-رورک از مفهوم حجم برخورد برای محاسبه احتمالی برخورد استفاده میکند. بجای محاسبه اینکه موقعیت مرکز قطره کوچکتر در حجم برخورد قطره قرار دارد یا خیر، این الگوریتم احتمال وجود قطره کوچکتر در حجم برخورد را محاسبه میکند. مشخص است که قطره کوچکتر در جایی در المان فاز پیوسته با حجم V واقع است. اگر احتمال یکسانی از وجود قطره کوچک در هر جای سلول در نظر گرفته شود، آنگاه شانس قرار گیری قطره در حجم برخورد همان نسبت دو حجم برخورد و سلول محاسباتی خواهد بود. بنابراین احتمال برخورد قطره بزرگتر با قطره کوچکتر در سلول از معادله (460) به دست میآید.
معادله (460) میتواند برای پارسلها نیز به کار رود که در آن n1 و n2 تعداد پارسلهای کالکتور و کوچکتر قرار دارند. میانگین مورد انتظار قطرات کالکتوری که تحت برخورد قرار میگیرند از رابطه (461) به دست میآید. معمولا تعداد واقعی برخوردها با تعداد میانگین مورد انتظار برابر نیست. طبق روش او-رورک توزیع احتمالی تعداد برخوردها از توزیع پوآسون پیروی میکند (معادله 462). در این معادله n تعداد برخورد بین قطرات کالکتور و سایر قطرات میباشد.

برای هر گام زمانی DPM، تعداد میانگین برخورد مورد انتظار برای هر زوج پارسلهای رهگیری شده در هر المان محاسبه میشود. نمونه تصادفی از توزیع پوآسون برای تشخیص برخورد یا عدم برخورد زوج پارسلها، محاسبه میشود.
عواقب برخورد
پس از تعیین برخورد دو پارسل لازمست پیامد برخورد آنها نیز مشخص شود. به طور کلی نتیجه برخورد قطرات ادغام (Coalescence) است و اگر برخورد به صورت مایل اتفاق بیافتد پرش (Bouncing) را به دنبال خواهد داشت. در قاب مرجع مورد استفاده احتمال ادغام قطرات میتواند به انحراف (Offset) مرکز قطره کالکتور و مسیر قطره کوچکتر بستگی داشته باشد. انحراف بحرانی تابعی از عدد وبر برخوردی و شعاعهای قطرات کالکتور و کوچکتر است که در روش او-رورک با استفاده از معادله (463) محاسبه میشود. در این معادله f تابعی از r1/r2 تعریف شده در رابطه (464) میباشد.
مقدار پارامتر برخورد واقعی، b، با (r1+r2)√Y برابر است. Y از یک عدد تصادفی بین صفر و یک انتخاب میشود. مقدار محاسبه شده b با مقدار bcrit مقایسه میشود و اگر b<bcrit باشد، آنگاه نتیجه برخورد ادغام خواهد بود. معادله (462) تعداد قطرات کوچکتری که با قطره جمع کننده ادغام شدهاند را مشخص میکند. مشخصات قطرات ادغام شده با استفاده از قوانین بقای اصلی تعیین میشود.
در مورد برخورد خراشان (Grazing Collision)، سرعتهای جدید براساس قوانین بقای ممنتم و انرژی محاسبه میشوند. البته فرض بر اینست که بخشی از انرژی جنبشی قطرات به خاصر چسبندگی و تولید ممنتم زاویهای تلف میشود. این اتلاف انرژی به b یا همان پارامتر انحراف برخورد وابسته است. او-رورک با استفاده از اشکال فرضی برای اتلاف انرژی معادله (465) را برای محاسبه سرعت جدید پیشنهاد داد. این معادله برای هر یک از مؤلفههای سرعت مورد استفاده قرار میگیرد. سایر خصوصیات قطره در برخورد خراشان بدون تغییر باقی میماند.
اگر ادغام قطرات در نظر گرفته نشود، پیامد برخورد ذرات یک برخورد مرکزی است. نقطه برخورد ذرات نیز به صورت تصادفی به عنوان یک نقطه روی خطی که مرکز دو قطره را به هم متصل میکند و در فصل مشترک سطوح ذرات هم واقع است، انتخاب میشود. در قاب مرجع قطره جمع کننده، جهت برخورد با بردار اصلی n نشانه گیری شده در جهت خط اتصال مرکز قطره جمع کننده و نقطه برخورد تعیین میشود. بنابراین براساس معادلات بقای ممنتم و انرژی، سرعت پسا-برخوردی (Post-Collisional) ذرات در جهت n با استفاده از معادله (466) به دست میآید [2].

m1 و m2به ترتیب جرم ذرات 1 و 2 و K، ضریب ارتجاع (Restitution Coefficient) در معادله (466) هستند. k=1 یک برخورد ایدهآل الاستیک است در حالیکه یک برخورد کاملا پلاستیک در k=2 اتفاق میافتد. قابل توجه است که تنهای اندازه سرعتهای هم جهت با n تغییر پیدا میکنند.
:[1]
P. J. O’Rourke. “Collective Drop Effects on Vaporizing Liquid Sprays”. PhD thesis. Princeton University, Princeton, New Jersey. 1981
:[2]
W. Gumprich, M. Chrigui, M. Braun, A. Sadiki. “Evaluation of collision models applied to varying dense particle jets flows”. 7th International Conference on Multiphase Flow. Tampa, FL: May 30 – June 4, 2010
https://www.researchgate.net/figure/Regimes-of-droplet-droplet-collision-a-coalescence-b-bouncing-c-reflexive_fig8_320458671