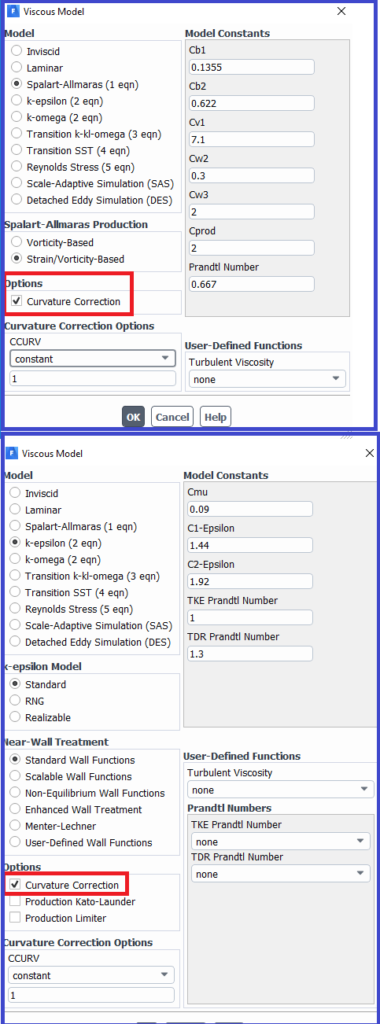
تابع اصلاح انحنا (Curvature Correction)

تابع اصلاح انحنا برای مدل‌ اسپالارت-آلماراس و مدل‌های دو معادله‌ای

Curvature Correction for the Spalart-Allmaras and Two-Equation Models

در حال به روز رسانی

تابع اصلاح انحنا (Curvature Correction) صرفا برای مدل اسپالارت-آلماراس و مدل‌های دو معادله‌ای توسعه یافته است. عدم حساسیت مدل‌های لزجت گردابه‌ای به انحناء خطوط جریان و یا چرخش جریان که نقش چشمگیری در بسیاری از جریان‌های آشفته بازی می‌کنند، باعث بروز مشکل قابل توجهی در حل میدان جریان می‌شود. از این رو در نرم افزار Fluent یک اصلاحیه ترم تولید آشفتگی به منظور حساس کردن مدل‌‎های آشفتگی زیر به اثرات انحنا خطوط جریان یا چرخش سیستم قابل دسترس است:

قابل توجه است مدل‌های آشفتگی K-E RNG & Realizable به خودی خود از ترم‌های مستقلی برای اعمال اثرات چرخش یا دوران برخوردار هستند. بنابراین از گزینه اصلاح انحنا باید با احتیاط و اساسا برای تکمیل عملکرد این دو مدل استفاده شود.

تاریخچه:

اسپالارت (Spalart) و شر (Shur) و همچنین شر و همکاران اصلاحیه‌ای برای ترم تولید مدل آشفتگی یک معادله‌ای اسپالارت-آلماراس استخراج کردند که اثرات انحنا خطوط جریان و چرخش جریان در محاسبات را لحاظ می‌کند. بر همین اساس یک اصلاحیه‌ی دیگری نیز برای ترم تولید که قادر است مدل‌های آشفتگی دو معادله‌ای را نیز به انحنا خطوط و چرخش جریان حساس کند توسط اسمیرنف (Smirnov) و منتر(Menter) توسعه یافته است.

فرمولاسیون تابع اصلاح انحنا (Curvature Correction)

تابع تجربی که توسط اسپالارت و شر برای محاسبه اثرات چرخش پیشنهاد شده است بصورت معادله (1) تعریف می‌شود. این تابع همانند یک تقویت کننده برای ترم تولید عمل می‌کند. اما مقدار آن در نرم افزار Fluent توسط رابطه (2) محدود می‌شود.

تابع اصلی f_r از صفر (به عنوان مثال برای انحنای محدب قوی همچون جریان‌های پایدار، بدون تولید آشفتگی) تا 1.25 (برای انحنای مقعر شدید همراه با تولید آشفتگی پیشرفته) متغیر است. محدوده پایینی بخاطر ملاحظات پایداری حل عددی اعمال نمی‌شود. همچنین لازمست از محدوده بالایی بخاطر تولید بیش از حد لزجت گردابه‌ای در جریان متشکل از چرخش/انحنای بی ثبات کننده، پرهیز نمود. محدودگر مخصوص 1.25 نتایج مناسبی را برای حالت‌های متفاوت حل شده توسط مدل SST (همچون جریان U-Turn، جریان در هیدروسیکلون‌ها و گردابه‌های نوک بال) به همراه داشته است.

C_scale یا همان C_curve در معادله (3) برای تعیین اثر قدرت اصلاح انحنا (Curvature Correction) در جریان‌های خاص تعریف می‌شود. طبق پیش فرض این مقدار 1 است. این مقدار می‌تواند بصورت یک عدد ثابت یا یک UDF تعریف شود. نکته مهم اما اینست که C_scale یا همان C_curve همواره باید مثبت باشد.

با فرض اینکه تمام متغیرها و مشتقات آن‌ها نسبت به یک قاب مرجع محاسبات تعریف می‌شوند که با نرخ Ω^Rot دوران می‌کنند، آرگومان‌های ^*r و ^~r در تابع f_rotation بصورت معادلات (5) و (6) تعریف می‌شوند. در معادله (6) اولین ترم داخل براکت معادل شیب دوم سرعت (در این حالت مشتق لاگرانژی تانسور نرخ کرنش) و ترم دوم داخل براکت اندازه دوران سیستم می‌باشد. نرخ کرنش و تانسور ورتیسیته نیز بصورت معادلات (7) و (8) تعریف می‌شوند.

مخرج معادله (6)، ^~D، برای مدل اسپالارت-آلماراس بصورت معادله (11) می‌باشد. برای سایر مدل‌های آشفتگی (روابط اسمیرنف و منتر) از معادله (3) برای محاسبه مخرج معادله (6) استفاده می‌شود.

ثوابت تجربی c_r1، c_r2 و c_r3 در معادله (1) عبارتند از:

به ترتیب 1، 12 و 1 برای مدل اسپالارت-آلماراس
به ترتیب 1، 2 و 1 برای سایر مدل‌های آشفتگی و براساس آزمایشات انجام شده.

کلام آخر

قابل توجه است تابع اصلاح انحنا به شدت به تغییرات در جهت تانسور نرخ کرنش وابسته است. بنابراین این تابع تنها در نواحی جریان برشی (لایه مرزی منحنی، لایه‌های اختلاط، جریان‌های گردابی و غیره) با معنی است.

در نواحی متشکل از نرخ کرنش برشی صفر یا خیلی کم، تابع مذکور می‌تواند تغییرات شدیدی داشته باشد. به هر صورت این مهم هیچ پیامدی ندارد. چراکه تابع اصلاح انحنا در ترم تولید معادلات انرژی جنبشی آشفتگی ضرب می‌شود که برای نرخ کرنش برشی محو شونده، صفر یا خیلی کم است.

بازگشت

مطالب مرتبط

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ

Ansys Fluent