SAS و DES؛ مدل‎های آشفتگی ترکیبی

مدل‌های آشفتگی ترکیبی SAS و DES

SAS and DES; Turbulence Hybrid Models

SAS و DES مدل‎های آشفتگی ترکیبی، مهمترین‌فرمولاسیون ترکیبی مدل‌های آشفتگی RANS-LES به شمار می‌روند. البته در ابتدا به نظر می‌رسد مفاهیم متوسط گیری رینولدز در روش‌های RANS و فیلترینگ فاصله‌ای (Spatial Filtering) در روش‌های LES با هم سازگار نیستند. چراکه ترم‌های اضافی متفاوتی در معادلات ممنتم (تنش‌های رینولدز و تنش‌های زیر شبکه) را طلب می‌کنند. از این رو باید از مدل‌های ترکیبی (هیبریدی) زیر که براساس یک دسته از معادلات ممنتم متشکل از بخش‌های LES و RANS توسعه یافته‌اند استفاده شود. 

• Scale Adaptive Simulation: SAS
• Detached Eddy Simulation: DES
• Shield Detached Eddy Simulation: SDES
• Stress-Blended Eddy Simulation: SBES

زمانیکه یک مدل آشفتگی در معادلات ممنتم ناویراستوکس  (به عنوان یک ترم چشمه) تعریف می‌شود دیگر حامل هیچ گونه اطلاعاتی در مورد مقادیر میانگین آن‌ها نمی‌باشد. نکته قابل توجه اینکه متداول‌ترین مدل‌های آشفتگی، هم RANS و هم LES، مدل‌های لزجت آشفتگی (گردابه‌ای) هستند که جایگزین تنش‌های رینولدز یا تنش‌های زیر شبکه در معادلات میانگین گیری شده RANS یا فیلتر شده LES می‌شوند. بنابراین پس از تعریف لزجت گردابه‌ای (لزجت آشفتگی) معادلات ممنتم RANS و LES رسما یکسان می‌شوند با این تفاوت که محاسبه لزجت گردابه‌ای توسط مدل‌های آشفتگی مختلفی صورت می‌پذیرد. این قابلیت به فرمولاسیون مدل‌های ترکیبی آشفتگی این اجازه را می‌دهد تا بین مودهای RANS و LES سوئیچ کند بدون آنکه به تغییری در ساختار معادلات ممنتم منجر شود. در واقع مدل‌های SAS و DES مدل‌های آشفتگی ترکیبی مجهز به مودهای RANS و LES هستند.

مدل‌های آشفتگی ترکیبی Scale-Adaptive Simulation: SAS

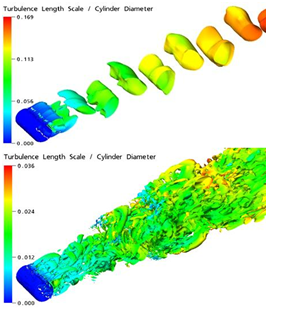
مدل آشفتگی شبی سازی تطبیق مقیاس (Scale-Adaptive Simulation: SAS) فرمولاسیون بهبود یافته‌ای از مدل‌های Unsteady RANS: URANS می‌باشد که اجازه می‌دهد طیف‌های آشفتگی در جریان‌ها ناپایا با وضوح بسیار بیشتری شبیه سازی شوند. شکل زیر مقایسه بین شبیه سازی جریان عبوری از روی یک سیلندر بین دو روش URANS-SST (تصویر بالا) و مدل ترکیبی SAS-SST (تصویر-پایین) را نشان می‌دهد. همانطور که در این شکل پیداست، در شبیه سازی به روش URANS-SST تنها مقیاس‌های بزرگ شبیه سازی شده‌اند در حالیکه در روش SAS-SST شاهد نمایش طیف‌های وسیعی از گردابه‌ها در نواحی جدایش جریان هستیم. 

در واقع مفهوم SAS براساس تعریف مقیاس طول (Length-Scale) ون کارمن (von Kármán )  در معادله مقیاس آشفتگی بیان شده است. مقیاس طول ون کارمن به مدل SAS اجازه می‌دهد که بصورت دینامیکی ساختار گردابه‌ها را در RANS تنظیم کند. حل مسئله با این روش رفتاری LES مانند در نواحی میدان جریان را نتیجه می‌دهد. در عین حال نیز توانمندی‌های استاندارد RANS در نواحی جریان پایدار را نیز شامل می‌شود. 

معادلات انتقال برای مدل SAT-SST

از یک دیدگاه بسیار مهم، تمامی مدل‌های دو معادله‌ای موجود از فقدان یک معادله انتقالی دقیق و زیربنایی برای مدلسازی دقیق ترم به ترم رنج می‌برند. علت این ضعف آنست که معادله انتقالی ε مقیاس‌های بزرگ بجز مقیاس‌های اتساع (Dissipative Scale) را نمی‌تواند توصیف کند. به هر صورت هدف از توسعه مدل‌های دو معادله‌ای، مدلسازی تأثیر حرکات گردابه‌های بزرگ روی جریان متوسط می‌باشد. به دلیل نبود یک معادله دقیق، معادلات ε و ω بطور مشابه و همانند معادله انرژی جنبشی آشفتگی، k، با استفاده از آرگومان‌های صرفا ابتکاری و اکتشافی شبیه سازی می‌شوند.

تقریب منسجم‌ و با ثباتی برای فرموله کردن معادله مقیاس توسط روتا (Rotta) ارائه شده است. بجای استفاده از آرگومان‌های ابعادی و ابتکاری، روتا یک معادله انتقالی برای مقیاس طول و انرژی جنبشی آشفتگی به دست آورد. در حقیقت معادله روتا بیانگر مقیاس‌های بزرگ آشفتگی بوده و بنابراین می‌تواند ترم به ترم مدلسازی را با دقت انجام دهد. معادلات انتقال مدل SAS-SST بکار رفته در Fluent براساس روش روتا برای K-ω SST  و بصورت زیر محاسبه می‌شود. 

همانطور که در بالا پیداست، معادلات مدل SAS-SST نشان داده شده در بالا تنها به خاطر اضافه شدن ترم Q_SAS در معادله انتقالی فرکانس گردابه، ω، با معادلات RANS-SST تفاوت دارد. همچنین پارامترهای σω و σω2 در معادله انتقالی ω، مقادیر مرتبط با رژیم K-ε در مدل SST می‌باشند. رابطه Q_SAS نیز در بالا نشان داده شده است. در واقع این ترم چشمه از ترم مشتق مرتبه دوم معادله انتقالی روتا سرچشمه می‌گیرد. مقادیر ثابت‌ها نیز در فرمولاسیون بالا درج شده است. روابط معرف L، مقیاس طول و Lvk، مقیاس طول ون کارمن نیز در فرمولاسیون فوق ارائه شده است.

مشتق سرعت u∂/∂y در رابطه Lvk بصورت ‘U تعریف می‌شود که مساوی با S، ثابت اسکالر تانسور نرخ کرنش می‌باشد. قابل توجه است که همان S بطور مستقیم در معادلات Q_SAS و ترم تولید آشفتگی Pk نیز حضور دارد. مشتق دوم سرعت “U برای فضای سه بعدی و با استفاده از مقدار لاپلاس سرعت بدست می‌آید. بنابراین L و Lvk تعریف شده هر دو برابر (ky) در بخش لگاریتمی لایه مرزی می‌باشند و K=0.41  ثابت ون کارمن است. مدل مذکور همچنین یک کنترل کننده مستقیم میرایی عدد موج بالا دارد که در روابط فوق نشان داده شده است. در واقع این محدود کننده متناسب با اندازه المان شبکه، Δ، بوده که بصورت ریشه دوم اندازه حجم کنترل Ω_CV محاسبه می‌شود. هدف از این محدود کننده، کنترل میرایی ریزترین نوسانات آشفتگی می‌باشد. 

مدل ترکیبی SAS همراه با سایر مدل‌های آشفتگی ω مبنا

روش ترکیبی SAS نه تنها با مدل SST بلکه با چندین مدل‌ دیگر آشفتگی ω مبنا نیز ترکیب شود که عبارتند از:

1- مدل‌های K-ω BSL ،K-ω Standard و مدل گذرای SST.

2- مدل‌های آشفتگی تنش رینولدز (RSM) مبتنی بر ω.

با اضافه نمودن توانمندی‌های SAS به یکی از مدل‌های فوق، ترم چشمه Q_SAS در معادله انتقالی ω قابل محاسبه می‌شود. اگر این قابلیت با مدل BSL ترکیب شود آنگاه ضرایب α و β در رابطه Lvx محدودگر، همان ضرائب مدل K-ω BSL خواهد بود. برای سایر ترکیبات، ضرائب مدل SST مورد استفاده قرار می‌گیرد. بعلاوهاین ضرایب در ترم SAS، اثرات تراکم‌پذیری را شامل نمی‌شوند. 

مدل‌های آشفتگی ترکیبی  detached Eddy Simulation: DES

در روش شبیه‌سازی گردابه‌های جدا شده (Detached Eddy Simulation: DES) مدل‌های URANS برای حل لایه مرزی بکار گرفته می‌شود در حالیکه از LES بمنظور شبیه سازی نواجی جدایش جریان استفاده می‌شود. مدل‌های RANS متعددی برای روش‌های DES وجود دارند که از جمله آن‌ها به مدل‌های اسپالارت-آلماراس، K-ε Realizable. K-ω BSL/SST و مدل گذرای SST اشاره نمود. ناحیه LES معمولا با هسته ناحیه آشفته -جائیکه مقیاس‌های آشفتگی ناپایا نقش مهمی بازی می‌کنند-در ارتباط هستند. در این نواحی مدل‌های DES مدل‌های زیرشبکه LES را پوشش می‌دهند. در حالیکه در نواحی نزدیک دیواره مدل‌های RANS بکار گرفته شده پوشش داده می‌شوند. 

مدل‌های DES اساسا برای جریان‌های محدود به دیواره (Wall-Bounded) و با رینولدزهای بالا توسعه یافته‌اند. چراکه هزینه (CPU و زمان) حل میداند جریان آشفته نزدیک به دیواره با استفاده از روش‌های LES بسیار زیاد است. تفاوت مدل‌های ترکیبی DES با LES تنها در حل میدان جریان نزدیک دیواره با استفاده از روش‌های RANS می‌باشد. به هر صورت همچنان استفاده از مدل‌های ترکیبی DES مستلزم برخورداری از پردازشگرهای پر قدرت محاسباتی است. به عنوان یک راهنمایی کلی پیشنهاد می‌شود که برای اغلب مسائل مهندسی از مدل‌های آشفتگی RANS متداول استفاده شود.

مدل‌های DES، ترکیبی از مدل‌های LES/RANS را برای کاربردهایی نظیر آئرودینامیک خارجی با اعداد رینولدز بالا را پیشنهاد می‌دهند. بدیهی است هزینه‌های محاسباتی زمانیکه از مدل‌های DES استفاده می‌شود کمتر از LES و بیشتر از RANS باشد. نکته آخر اینکه برای تولید آشفتگی تصادفی در ورودی‌ها در مدل‌های SAS و DES، همانند روش‌های مرتبط LES عمل می‌شود. 

مدل DES همرا با مدل اسپالارت آلماراس (Spalart-Allmaras)

مدل استاندارد اسپالارت-آلماراس از نزدیک‌ترین فاصله به عنوان تعریف مقیاس طول، d، استفاده می‌کند که نقش اصلی را در اندازه‌گیری سطح تولید و اتلاف لزجت آشفتگی بازی می‌کند. مدل DES پیشنهادی شر (Shur) مقدار d را در هر جایی با مقیاس طول آشفتگی d˜ تعریف شده در زیر جایگزین می‌کند:

که Δmax بزرگترین طول لبه برای یک المان شش وجهی مکعب مستطیل (برای سایر انواع المان‌ها نیز از مفهومی مشابه استفاده می‌شود) می‌باشد. ثابت تجربی Cdes نیز برابر با 0.65 تعیین شده است. برای شبکه‌های معمولی RANS با نسبت منظری بالا در لایه مرزی و جائیکه فاصله شبکه موازی با دیواره می‌باشد معمولا پارامتر δ تعریف می‌شود که مبین ضخامت لایه مرزی است، معادله فوق ضامن آنست که مدل DES در حل لایه مرزی همان مدل RANS باشد. به هرصورت در شرایط تعریف مبهم شبکه، اگر Δmax<δ باشد، محدود کننده DES می‌تواند مود LES را در لایه مرزی فعال کند حتی اگر شبکه به اندازی کافی برای شبیه سازی گردابه‌ها، کوچک نباشد. بنابراین فرمولاسیون جدیدی از DES در نرم افزار Fluent در دسترس است که مود RANS را در لایه مرزی نگاه می‌دارد. این مدل به Delayed DES یا DDES معروف است. در این مدل مقیاس طول آشفتگی d˜ بصورت زیر تعریف می‌شود:

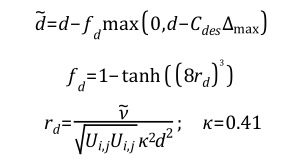
مدل DES همرا با مدل K-ε Realizable

این مدل DES همانند مدل K-ε Realizable شرح داده شده در اینجا می‌باشد.با این تفاوت که ترم اتلاف برای معادله K در مدل DES بصورت زیر تعریف می‎‌شود:

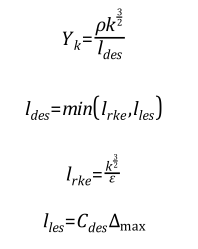
Δmax بزرگترین طول لبه برای یک المان شش وجهی مکعب مستطیل (برای سایر انواع المان‌ها نیز از مفهومی مشابه استفاده می‌شود) می‌باشد. Cdes=0.61 نیز ثابت کالیبراسیون است. اگر ldes=lrke شود آنگاه یک توصیف جدید برای ترم اتلاف در مدل K-ε Realizable مطرح می‌گردد. همانند DDES/Spalart-Allmarasِ، از مفهوم DDES برای مدل K-ε Realizable نیز می‌توان استفاده نمود که مود RANS را در لایه مرزی حفظ کند. برای این مفهوم طول ldes بصورت زیر بازتعریف می‌شود:

باید توجه داشت که fd مورد استفاده در معادله فوق همانند مدل اسپالارت-آلماراس تعریف می‌شود بجز اینکه مقدار ثابت از 8 به 20 تغییر کرده و ν˜ جانشین (ν + νt) در محاسبات Kd می‌گردد.

مدل DES همرا با مدل‌های K-ω BSL/SST

ترم اتلاف معادله انرژی تعریف شده در مدل‌های K-ω که در اینجا تشریح شده است برای مدل آشفتگی DES براساس تحقیق منتر (Menter) و بصورت زیر تعریف می‌شود:

Δmax بزرگترین طول لبه برای یک المان شش وجهی مکعب مستطیل (برای سایر انواع المان‌ها نیز از مفهومی مشابه استفاده می‌شود) می‌باشد. Cdes=0.61 نیز ثابت کالیبراسیون است. مقدار مقیاس طول آشفته (Turbulence Length Scale) نیز پارامتریست که رابطه متناظر آن در فرمولاسیون بالا نشان داده شده است. همچنین مدل‌های DES-BSL/SST گزینه‌ای (delayed Option)را برای مصون نگه داشتن لایه مرزی از محدودگر (Limiter) پیشنهاد می‌کنند. در این حالت FDES با استفاده از رابطه زیر بدست می‌آید: 

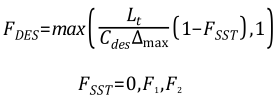
که F1 و F2 توابع وزنی مدل BSL/SST می‌باشند. البته به عنوان یک جایگزین، تابع پوشش (Shielding Function) مدل DES یا همان تابع IDDES نیز در نرم افزار Fluent وجود دارد. به هر حال مقادیر پیش فرض مربوطه در این نرم افزار همانند مدل DDES می‌باشد.قابل توجه است در کاربردهای DDES و IDDES،پارامتر fd مورد استفاده باز هم همانند مدل اسپالارت-آلماراس تعریف می‌شود بجز اینکه مقدار ثابت از 8 به 20 تغییر می‌کند. به هر صورت تاوبع وزنی FDDES بصورت زیر تعریف می‌شود:

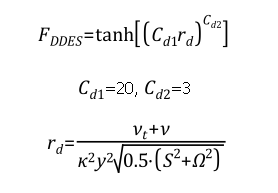
که S اندازه تابع نرخ کرنش، Ω اندازه تانسور سرعت، y فاصله تا دیواره و k=0.41 می‌باشد. 

مدل DES همرا با مدل‌ گذرای SST

مدل گذرای SST را نیز می‌توان با روش DES ترکیب نمود. ترم اتلاف معادله انتقالی انرژی جنبشی آشفتگی همانند همان مدل DES-BSL/SST می‌باشد. تمامی توابع پوششی نیز همانند معادلات نشان داده شده در قسمت قبل (مدل DES-BSL/SST) هستند. 

مدل (Improved Delayed Detached Eddy Simulation (IDDES

مدل IDDES یک مدل هیبریدی RANS-LES (شامل ترکیبی از تکنیک‌های موجود و جدید) می‌باشد که مدل شبیه سازی حل مقیاس (Scale-Resolving Dimulation) را برای جریان‌های همراه با رینولدزهای بالاتر، مناسب‌تر و منعطف‌تر می‌سازد. از آنجائیکه فرمولاسیون این مدل به نسبت پیچیده است و کاربردهای این مدل در مسائل پیش پا افتاده نیست، لذا از پرداختن به جزئیات آن خودداری شده است. علاقه‌مندان می‌توانند برای کسب اطلاعات بیشتر به مقالات شر و همکاران (Shure et all) و گریتسکوویچ و همکاران (Gritskevich et al) مراجعه کنند. در واقع مدل IDDES علاوه بر اهداف مدل‌های استاندارد DES، اهداف زیر را نیز دنبال می‌کند:

• فراهم نمودن پوشش مناسب در برابر جدایش القایی شبکه ((Grid Induced Separation (GIS) همانند مدل DDES و 
• مجوز اجرا کردن مود WMLES در شرایط مرزی ورودی ناپایا برای شبیه سازی لایه مرزی در حالت ناپایا.

مدل IDDES برای این طراحی شده است که مدل LES بتواند لایه مرزی را در رینولدزهای بالاتری نسبت به مدل‌های استاندارد خود شبیه سازی کند. به عنوان یک جایگزین برای شرایط ورودی ناپایا می‌توان از یک مانع استفاده کرد (همانند قرار دادن یک ریب یا مانع در داخل یا بالادست جریان در لایه مرزی).

IDDES مورد استفاده در نرم افزار Fluent براسا مدل‌های K-ω BSL/SST می‌باشد. شبیه مدل DES، معادله انتقال k در مدل BSL/SST نیز به منظور پوشش اطلاعات در فواصل شبکه محلی تصحیح شده است. همچنین در حالتیکه ابعاد شبکه به اندازه کافی ریز باشد این مدل به مود LES سوئیچ می‌کند. به هرصورت هدف اصلی پوشش لایه مرزی پایدار (به معنی عدم وجود شرایط ورودی ناپایدار و یا موانع تولید ناپایداری در بالادست) در مود RANS می‌باشد. به منظور پرهیز از تأثیرپذیری مدل BSL/SST تحت چنین شرایطی، تابع IDDES محافظی (Shielding) شبیه مدل DDES تولید می‌کند. به این معنی که تلاش می‌کند لایه مرزی را در مود RANS پایدار نگه دارد حتی اگر شبکه ریز باشد. در صورت حل لایه مرزی با استفاده از WMLES، لازمست شرایط ورودی ناپایدار ایجاد شود (با یکی از روش‌های ورتکس متد یا سنتزایزر طیفی). این مدل همچنان می‌تواند با گزینه ELES نیز بکار گرفته شود.

مدل IDDES-BSL/SST بر پایه ترم اتلاف معادله انرژی K-ω SST/BSL توسعه یافته است. لازم به توضیح است که معادلات ω در این مدل‌ها همچنان بدون تغییر باقی می‌مانند. 

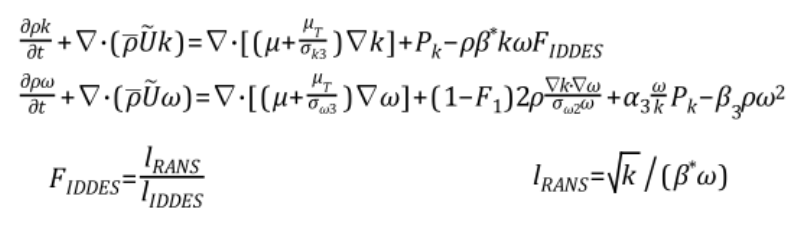
که F_IDDES بر مبنای نسبت مقیاس طول آشفته RANS به مقیاس شبکه LES (در رابطه بالا) تعیین می‌گردد. باید توجه داشت مقیاس طول زیر شبکه، Δ، در اینجا با فرمولاسیون DES متفاوت است. در فرمولاسیون IDDES از یک رابطه کلی‌تر برای Δ استفاده می‌شود که ترکیبی از مقیاس شبکه محلی و فاصله تا دیواره dw می‌باشد. hmax نیز بزرگترین طول لبه برای یک المان شش وجهی مکعب مستطیل (برای سایر انواع المان‌ها نیز از مفهومی مشابه استفاده می‌شود) می‌باشد. مجددا یادآوری می‌گردد که به دلیل پیچیدگی روابط از پرداختن به جزئیات آن‌ها در این قسمت صرف نظر شده است.

بازگشت

مطالب مرتبط

حل میدان‌های جریان‌های غیر لزج، آرام و آشفته با استفاده از نرم‌افزارهای CFD

مدلسازی آشفتگی با استفاده از روش‌های RANS

معرفی مدل آشفتگی تنش رینولدز (RSM)

مدلسازی آشفتگی با استفاده از روش‌های LES

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ