پردازش دیواره پیشرفته
Enhanced Wall Treatment
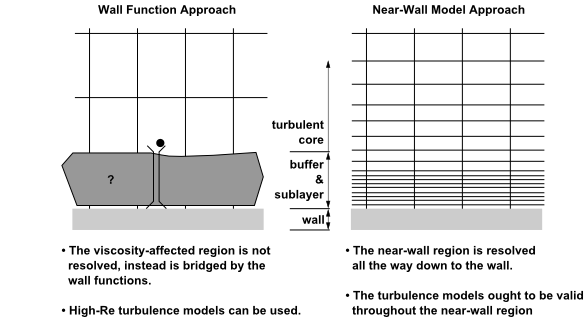
پردازش دیواره پیشرفته (Enhanced Wall Treatment) برای معادله ε، یک روش مدلسازی نزدیک دیواره است. این روش ترکیبی از یک مدل دولایه (Two-Layer) با توابع دیواره پیشرفته (Enhanced Wall Function) میباشد. اگر شبکه نزدیک دیواره به اندازهای ریز باشد که بتواند زیر لایه لزج را حل کند (به عبارتی به اندازهای باشد که y+≈1 شود)، آنگاه پردازش دیواره پیشرفته همان مدل سنتی ناحیهای دولایه (که در ادامه تشریح شده است) خواهد بود. به هر صورت چالش تولید شبکه مناسب برای تمام لایه مرزی ممکن است به محاسبات بسیار زیاد منجر شده و هزینه را بشدت افزایش دهد.
در حالت ایدهآل استفاده از فرمولاسیون نزدیک دیواره همراه با شبکههای درشتتر لایه مرزی (معمولا به عنوان شبکههای تابع دیواره شناخته میشود) و یا شبکههای ریزتر (شبکههای رینولدز پایین برای مدلسازی نزدیک دیواره) مطلوب است. بنابراین نباید سراغ شبکههای متوسطی که اولین گره محاسباتی نزدیک به دیواره نه در ناحیه کاملا آشفته قرار میگیرد (که توابع دیواره در آنجا مناسب هستند) و نه کاملا نزدیک به دیواره که در آن y+≈1 است (جائیکه ملاحظات عدد رینولدز پایین کافیست) و خطای زیادی دارد، رفت.
برای برخورداری از یک مدلسازی نزدیک دیواره که در آن رویکرد دولایه استاندارد برای شبکه خوب نزدیک به دیواره را به همراه داشته باشد و در عین حال از دقت شبکه تابع دیواره نکاهد، میتوان مدل دولایه را با توابع دیواره پیشرفته ترکیب کرد. کاری که در نرم افزار Fluent انجام شده است. در ادامه جزئیات این راه حل توضیح داده شده است.
مدل دولایه برای پردازش دیواره پیشرفته
در مدل نزدیک دیواره نرم افزار Fluent، ناحیه نزدیک به دیواره و تحت تأثیر لزجت (Viscosity-Affected Near-Wall Region) تا زیرلایه لزج بطور کامل حل میشود. رویکرد دولایه بخشی جدایی ناپذیر از پردازش دیواره پیشرفته است که برای تعیین نرخ اتلاف، ε، و لزجت آشفتگی در المانهای نزدیک دیواره استفاده میشود. در این رویکرد کل دامنه به دو ناحیه تحت تأثیر لزجت و کاملا آشفته تقسیم میشود. مرز این دو ناحیه بوسیله عدد رینولدز آشفته مبتنی بر فاصله تا دیواره نشان داده شده در معادله (1) مشخص میشود. در این معادله y فاصله مرکز المان تا دیواره میباشد. در نرم افزار Fluent پارامتر y به عنوان فاصله تا نزدیکترین دیواره (معادله 2) تفسیر میشود.

تفسیر بالا به y اجازه میدهد تا برای میدان جریان در هندسههای پیچیده همراه با دیوارههای متعدد بصورت یکتا تعریف شود. علاوه بر اینy تعریف شده در این مسئله مستقل از هندسه شبکه میباشد.
در نواحی کاملا آشفته (Rey>Re*y; Re*y=200) از مدلهای k-ε یا RSM استفاده میشود. در حالیکه در ناحیه نزدیک دیواره تحت تأثیر لزجت (Rey<Re*y)، مدل یک معادلهای ولفشتاین (Wolfstine) بکار گرفته میشود. در این مدل یک معادلهای معادلات ممنتم و انرژی جنبشی آشفتگی، k، بدون تغییر باقی میمانند. اما لزجت آشفتگی μt از رابطه (3) بدست میآید. مقیاس طول حاضر در معادله (3) با استفاده از معادله (4) محاسبه میشود. این فرمولاسیون دولایه برای لزجت، بخشی از محاسبات پردازش دیواره پیشرفته را به خود اختصاص داده که در آن لزجت دولایه، μt,2layer، به آهستگی با لزجت آشفتگی عدد رینولدز بالا، μt،از ناحیه دیگر ترکیب میشود (معادله 5). چگونگی محاسبه μt در معادله (5) در قسمت مدلهای آشفتگی RSM و k-ε توضیح داده شده است.
محاسبه ε
تابع ترکیب λε به این ترتیب تعریف میشود که دور از دیواره 1 و در مجاورت دیواره صفر باشد (معادله 6). ثابت A نیز عرض تابع ترکیب را تعریف میکند. با تعریف عرض که در آن λε با توجه به تغییرات ΔRey باید در 1% مقدار دور از دیواره آن باشد. مقدار A از رابطه (7) بدست میآید. معمولا ΔRey بین 5% تا 20% Re*y در نظر گرفته میشود. هدف اصلی تابع λε جلوگیری از همگرایی حل در زمانیکه μt بدست آمده در لایه خارجی با μtارائه شده توسط مدل ولفشتاین (در مرز ناحیه تحت تأثیر لزجت) مطابقت ندارد، میباشد.
میدان ε در ناحیه تحت تأثیر لزجت از رابطه (8) بدست میآید. مقیاسهای طول حاضر در رابطه (8) از معادله چن (Chen) و پاتل (Patel) بدست میآید (معادله 9). اگر کل میدان جریان در داخل ناحیه تحت تأثیر لزجت (Rey<200) باشد، آنگاه ε با حل معادله انتقال بدست نمیآید. بجای آن با استفاده از رابطه (8) محاسبه میشود. نرم افزار Fluent از روشی برای ترکیب ε استفاده میکند که مشابه همان روش توضیح داده شده برای μt است تا اطمینان حاصل شود که انتقال آرامی بین ε محاسبه شده از معادله جبری در ناحیه داخلی و ε حاصل از حل معادله انتقال در ناحیه خارجی اتفاق بیفتد.

پردازش دیواره پیشرفته برای معادلات ممنتم و انرژی
برای داشتن روشی که کاربردهایش در ناحیه نزدیک دیواره (یعنی زیر لایه لزج، لایه بافر و ناحیه کاملا آشفته) نیز بسط پیدا کند لازمست قانون دیواره بصورت یک قانون دیواره تنها فرموله شود. نرم افزار Fluent با ترکیب قانون دیواره خطی (آرام) و لگاریتمی (آشفته) و با استفاده از تابع پیشنهادی توسط کادر (Kader) به این مهم دست یافته است (معادله 10). بطور مشابه رابطه مناسبی برای +du+/dy بصورت معادله (12) تعریف میشود.

این تقریب به قانون کاملا آشفته اجازه میدهد تا به راحتی اصلاح شده و برای محاسبه سایر اثرات نظیر گرادیانهای فشار یا ویژگیهای متغیر توسعه یابد. همچنین این رابطه صحت رفتار جانبی مقادیر بزرگ و کوچک و پروفایل سرعت در شرایطی که y+ در داخل ناحیه بافر میافتد (+y بین 3 و 10 میباشد) را تضمین میکند.
پردازش دیواره پیشرفته با ترکیب هموار فرمولاسیون لایه لگاریتمی با معادله لایه آرام توسعه یافته است. قانون دیواره آشفته پیشرفته برای جریانهای تراکم پذیر همراه با انتقال حرارت و گرادیانهای فشار با ترکیب روشهای وایت – کریستف (White – Cristoph) و هانج (Huang) و همکاران استخراج میشود.
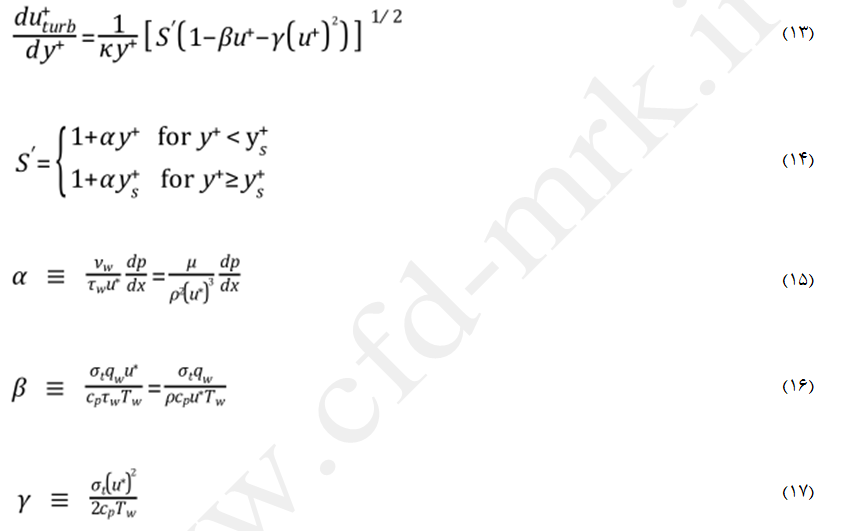
معادلات انرژی
Y+s مکانی است که شیب قانون لگاریتمی در آن ثابت است. طبق پیشفرض y+s=60 است. ضریب α در معادله (14) بیانگر تأثیرات گرادیانهای فشار میباشد در حالیکه β و γ نشانگر اثرات گرما هستند. معادله (13) یک معادله دیفرانسیل معمولی هستند که بصورت تحلیلی در نرم افزار Fluent حل میشوند. اگر α، β و γ صفر باشند، آنگاه حل تحلیلی به قانون دیواره لگاریتمی آشفته کلاسیک منجر میشود.
قانون دیواره آرام از رابطه (18) محاسبه میشود. باید توجه داشت که معادله (18) تنها اثرات ناشی از گرادیانهای فشار، α، را شامل میشود. به عبارت دیگر از اثرات ویژگیهای متغیر ناشی از انتقال حرارت و تراکمپذیری صرفنظر شده است. علت چشم پوشی آنست که این اثرات تأثیرات کمی در نزدیکی دیواره دارند. همچنین معادله (19) انتگرال معادله (18) میباشد. توابع پیشرفته از همان روش توسعه یافته برای +u پیروی میکنند. فرمولاسیون یکپارچه گرمای دیواره پروفیلهای آرام و لگاریتمی (آشفته) را براساس متد کادر (Kader) ترکیب میکند (معادله 20). نمادهای Tp و .q همان نمادهای تعریف شده در تابع دیواره حرارتی استاندارد هستند.

Pr: عدد پرانتل ملکولی
جدا از فرمولاسیون + T در معادله (20) توابع دیواره حرارتی پیشرفته از همان منطق توابع دیواره حرارتی استاندارد پیروی میکند. بنابراین توابع دیواره حرارتی آرام و آشفته بصورت معادلات (22) و (23) تعریف میشوند. در رابطه (23) u+c مقدار + u در تقاطع ساختگی بین نواحی آرام و آشفته میباشد. تابع P از همان روش تشریح شده در توابع دیواره استاندارد تعریف میشود.
فرآیندی مشابه برای توابع دیواره گونههای شیمیایی در پردازش دیواره پیشرفته بکار میرود. در این حالات اعداد پرانتل در معادلات (22) و (23) بوسیله اعدا اشمیت جایگزین میشوند (اینجا).
تعریف شرایط مرزی برای انرژی جنبشی آشفتگی همانند توابع دیواره استاندارد هستند. به هر صورت ترم تولید انرژی جنبشی آشفتگی، Gk، با استفاده از گرادیانهای سرعت سازگار با قانون دیواره پیشرفته (معادلات 10 و 12) و با اطمینان از اینکه فرمولاسیون در تمام ناحیه نزدیک به دیواره صحیح باشد، محاسبه میشود.
کلام آخر
پردازش دیواره پیشرفته (Enhanced Wall Treatment) برای تمام مدلهای معادلات ε (بجز مدل Quadratic RSM) در دسترس است. یک فرمولاسیون جایگزین برای مدلهای k-ε، پردازش منتر-لچنر (Menter-Lechner) میباشد که یک پردازش نزدیک دیواره غیر حساس به y+ است. این پردازش نزدیک دیواره غیر حساس به دیواره طبق پیشفرض نرم افزار Fluent در مدلهای آشفتگی زیر بکار میرود:
- مدلهای معادله ω
- مدل آشفتگی اسپالارت-آلماراس
باید توجه داشت یک ترکیب جایگزین در مقایسه با ترکیب کادر (Kader) برای +u و+ du+turb/dy در مدل اسپالارت-آلماراس و پردازش نزدیک دیواره بهبود یافته برای مدلهای آشفته مبتنی بر معادله ω بکار رفته که پیشفرض نرم افزار Fluent است.
**آموزش تئوری و موارد کاربرد Yplus، YStar، توابع دیواره (Wall Function) و مدلسازی نزدیک دیواره در نرم افزار Ansys Fluent**
مطالب مرتبط
توابع دیواره استاندارد (Standard Wall Functions)
توابع دیواره مقیاسپذیر (Scalable Wall Functions)
توابع دیواره نامتعادل (Non-Equilibrium Wall Functions)
پردازش نزدیک دیواره منتر- لچنر (Menter-Lechner Near-Wall Treatment)