مدل کانک (Kuhnke Model) در DPM

مدل کانک

Kuhnke Model

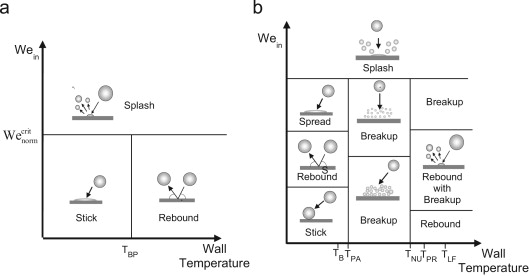
مدل کانک (Kuhnke Model) در DPM همانند مدل استانتن-روتلند (The Stanton-Rutland Model) اندرکنش قطره با دیواره را بر اساس رژیم‌های مختلف برخورد و دمای دیواره شبیه‌سازی می‌کند. در این مدل سرنوشت‌های مختلف قطره پس از برخورد با دیواره در شکل پایین نشان داده شده است. این مدل تمامی پدیده‌های متناسب با نوع و شدت برخورد را با دسته‌بندی کلی در چهار رژیم و براساس مقادیر بدون بعد K و ^*T (معادلات 257 و 260) پوشش می‌دهد. پخش یا رسوب (Spread or Deposition)، بازگشت (Rebound)، پاشش (Splash) و پاشش خشک (Dry Splash) یا همان فروپاشی حرارتی (Thermal Breakup) چهار رژیم تعریف شده در مدل مذکور هستند.

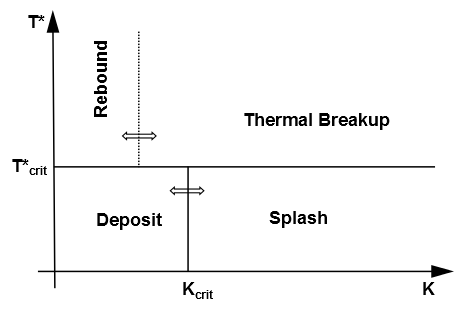
رژیم‌های مختلف سرنوشت برخورد قطره با دیواره

 

رفتار و شرایط حاکمیت رژیمهای مختلف در مدل کانک (Kuhnke Model) در DPM

رژیم‌های رسوبی و پاششی منجر به تشکیل یک فیلم دیواره می‌شوند که مقدار بدون بعد K طبق معادله (257) تعریف می‌شود.

We: عدد وبر براساس مؤلفه عمودی سرعت برخورد

La: عدد لاپلاس

ρ: چگالی قطره (Kg/m3)

d_p: قطر قطره (m)

V_pn: مؤلفه عمودی سرعت برخورد (m/s)

σ: تنش سطحی قطره (N/m)

µ: لزجت قطره (Kg/m-s)

Tw: دمای دیواره (K)

T_sat: دمای اشباع قطره (K)

بطور دقیق‌تر ویژگی رژیم‌ها در مدل کانک از قرار زیر است:

پاشش (Spread):

در این رژیم قطره به دیواره تحت شرایط زیر اضافه می‌شود:

• K<K_Crit و T^*<T^*_Crit
• K<KCrit و دیواره مرطوب باشد.

بازگشت (Rebound):

• K<K_Crit و T^*>T^*_Crit
• We<5 و دیوراه مرطوب باشد.

پاشش (Splash):

قطره در ابعاد کوچکتر اتمایزر می‌شود اگر: K>K_Crit باشد.

در رژیم پاشش، بسته به دمای دیواره و شرایط سطح آن، قطره برخورد کننده به دیواره ممکن است روی دیواره بنشیند و یک فیلم دیواره را تشکیل دهد یا اینکه کاملا اتمایزر شود (پاشش خشک یا فروپاشی حرارتی)

در ادامه چگونگی محاسبه پارامترهای گذرای بحرانی K_Crit و T^*_Crit توضیح داده شده است. انتقال وابسته به دمای دیواره توسط پارامتر دمای بحرانی T^*_Crit کنترل می‌شود که مقدار آن بین 1.1 تا 1.5 و بسته به کاربرد آن متغیر است. البته مقدار پیش فرض آن در نرم افزار Fluent برابر با 1 است. در نتیجه دمای انتقالی پیش فرض با دمای اشباع مایع یکی خواهد بود. البته مدل کانک مقادیر 1.1 را برای یک قطره و 1.16 را برای زنجیره‌ای از قطرات توصیه می‌کند. برای اکثر دوغاب‌های آب-اوره (Urea-Water Slurries) مقدار 1.4 برای T^*_Crit مناسب است ]1[.

دو مقدار بحرانی پارامتر K (که یکی مربوط به انتقال بین بازگشت و شکست حرارتی در دمای بالا، K_hot، و دیگری مربوط به انتقال بین رسوب و پاشش در دمای پایین، K_cold، می‌باشد.) به چندین پارامتر و شرایط دیواره (خشک یا مرطوب) بستگی دارد که عبارتند از:

شرایط دیوار مرطوب:

معادله (261) برای محاسبه K_Crit در شرایط دیوار مرطوب حاکم است.

h_f: ارتفاع فیلم دیواره (m)

d_p: قطر قطره (m)

مقادیر x، x₀، y_l، y_r، s و q ثوابتی هستند که مقدار آن‌ها در معادله (261) نشان داده شده است.

 

شرایط دیوار خشک:

معادله (265) برای محاسبه K_Crit در شرایط دیوار خشک حاکم است.

 

ε_a: زبری سطح بدون بعد R_a/d_p

R_a: زبری سطح (m) و برابر با میانگین قدر مطلق پستی بلندیها از میانگین سطح دیواره می‌باشد

ω: (در معادله 266) مقدار گذرای محدوده (Threshold) تابع مرکب می‌باشد که برابر با 0.99 در نظر گرفته شده و عرض ناحیه ترکیب است.

K_hot: بطور تصادفی از بین 20 تا 40 نمونه‌گیری می‌شود (معادله 267). در این معادله p بصورت تصادفی از بین صفر تا یک انتخاب می‌شود.

y_s: کسر جرمی پاشش (معادله 270)

 

رژیم بازگشت در مدل کانک (Kuhnke Model) در DPM

در رژیم بازگشت مؤلفه‌های سرعت بازگشت طبق روابط (272) و (273) محاسبه می‌شود.

V_rt: مؤلفه مماسی سرعت بازگشتی

V_rn: مؤلفه عمودی سرعت بازگشتی

V_pt: مؤلفه مماسی سرعت برخورد

V_pn: مؤلفه عمودی سرعت برخورد

e_n: ضریب انعکاس عمودی

We_o: مؤلفه عمودی عدد وبر پیش از برخورد

لازم به توضیح است زاویه انحراف قطره بازگشتی، ψ، بصورت اتفاقی از بین 90- تا 90 درجه از جهت برخورد انتخاب می‌شود.

رژیم پاشش در در مدل کانک (Kuhnke Model) در DPM

در شکل زیر رژیم پاشش نشان داده شده است. همانطور که در این شکل پیداست:

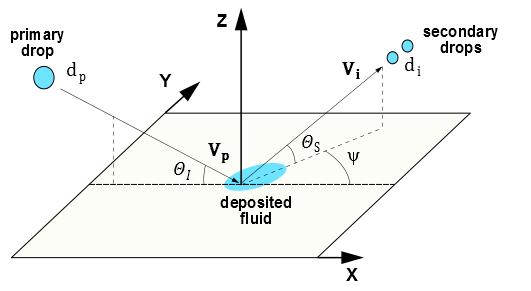
شماتیک رژیم پاشش در مدل کانک

d_p: قطر قطره برخورد کننده به دیواره،

V_p: سرعت برخورد قطره،

d_i: قطر قطره ثانویه پاشیده شده،

Vi: سرعت قطره ثانویه پاشیده شده،

θ_I و θ_S: زاویه قطره برخورد کنند و قطرات ثانویه از سطح دیواره و

Ψ: زاویه انحراف از جهت برخورد هستند.

 

قابل توجه است که بطور معمول اندازه گیری زوایای برخورد و انعکاس در مدل‌های استانتن/راتلند و کانک متفاوت از یکدیگر هستند.

تفاوت مدل کانک و استانتن راسلند:

• در مدل استانتن و راتلند: از جهت عمود بر دیواره
• در مدل کانک: از جهت مماس بر دیواره

به عنوان اولین گام قطر میانگین قطرات ثانویه پاشش از رابطه (275) محاسبه می‌شود. در گام دوم که اساسا از مدل استانتن/روتلند گرفته شده، قطر قطرات پاشیده شده، d_si، بطور تصادفی از معکوس تابع چگالی احتمالی ویبل Weibull_{CPD fi} که در رابطه (277) نشان داده شده نمونه‌گیری می‌شود.

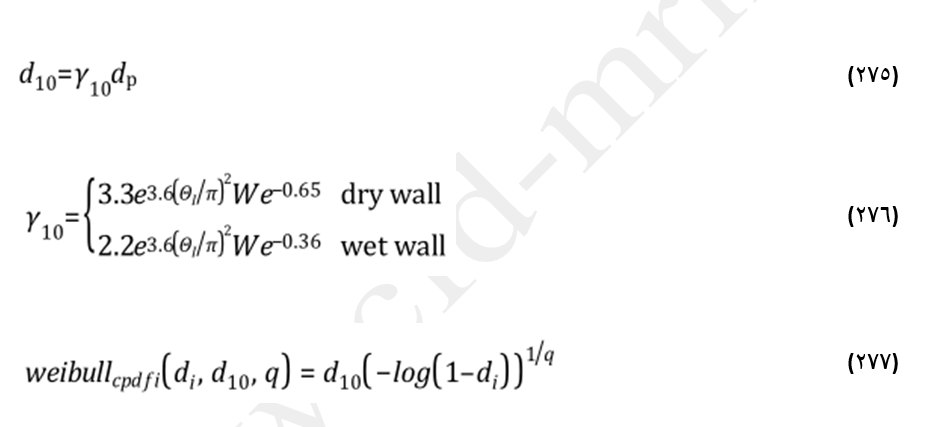
در روابط فوق d_p: قطر قطره اولیه (m)،

We: عدد وبر مؤلفه عمودی سرعت برخورد قطره به دیواره و

θ_i: زاویه تصادف در واحد رادیان هستند.

قابل توجه است که با q=2، روش محدود کننده تشریح شده در مدل استانتن در اینجا نیز کاربرد دارد. تعداد قطرات هر بخش پاشش با استفاده ز بالانس جرمی (معادله 243) محاسبه می‌شود.

سرعت متوسط قطرات پاشش V₁ از عدد بر ثانویه We_a1 و اندازه متوسط قطره d₁₀ و  با استفاده از معادله (278) محاسبه می‌شود. We_a0 و We_a1 نیز براساس سرعت‌های مطلق قطرات تعریف می‌شوند.

 

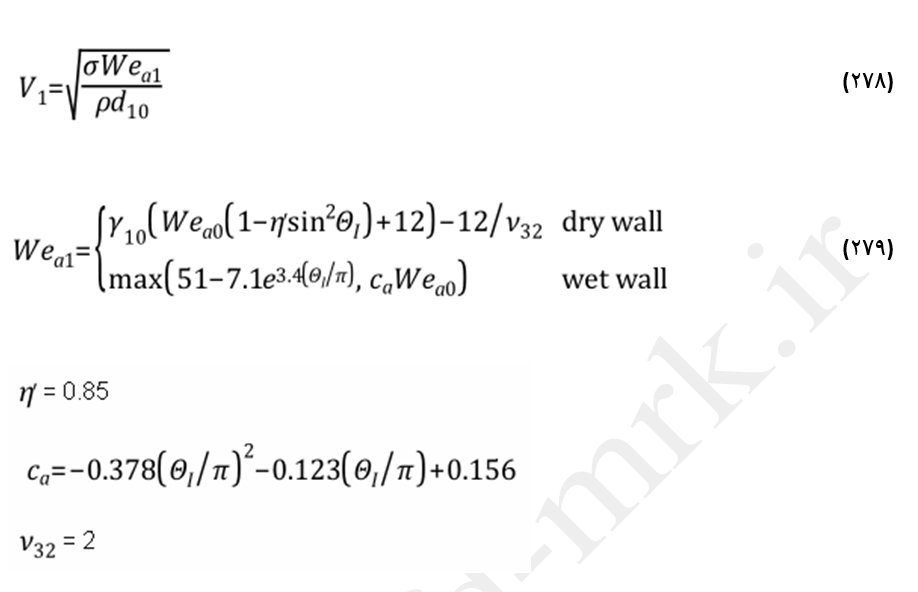
مشابه با قطرهای قطرات پاشیده شده، سرعت‌های آن‌ها، Vi، نیز بصورت تصادفی از معکوس تابع چگالی احتمالی ویبل با توزیع میانگین V₁ بدست می‌آیند. زاویه پس‌زنی (Ejection) که با θ_s نشان داده می‌شود، از مقدار میانگین θ^–_s و با فرض توزیع منطقی محاسبه می‌شود (معادله 280).

 

در معادله (280) زوایا برحسب درجه و بوسیله یک تابع چگالی احتمالی منطقی (رابطه 281) با σ_l=4 توزیع می‌شود.

ε_z: زبری سطح بدون بعد R_z/d_p

Rz: زبری سطح (m) و برابر با میانگین بیشترین اختلاف ارتفاع می‌باشد

 

:[1]

 F. Birkhold, U. Meingast, P. Wassermann, and O. Deutschmann. “Analysis of the Injection of Urea-Water-Solution for Automotive SCR DeNOx-Systems: Modeling of Two-Phase Flow and Spray/Wall-Interaction”. SAE Technical Paper 2006-01-0643. University of Karlsruhe. 2006.

 

 

 

 

بازگشت

مطالب مرتبط

مدل استانتن (Stanton) و روتلند (Rutland):

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ

Ansys Fluent