روش‌های حل مستقیم و تکراری

روش‌های حل مستقیم و تکراری دستگاه معادلات

Direct and Iterative Methods for solving system of equations

در حل عددی معادلات به روش ضمنی، لازمست که دستگاه معادلات {b}={x}[A]، در هر گام زمانی یا تکرار حل شود. روش‌های متعددی برای حل این دستگاه معادلات وجود دارد که کلاً به دو دسته روش‌های حل مستقیم و تکراری دسته بندی می‌شوند. در ادامه هر یک از این روش‌ها بطور مختصر توضیح داده شده است.

حل مستقیم در روش‌های حل مستقیم و تکراری

در روش حل مستقیم با پیدا کردن معکوس ماتریس ضرائب، ^1–[A]، مجهولات بصورت {x}=¹[A]^-1{b}به دست می‌آیند. لازم به یادآوری است که پیدا کردن معکوس ماتریس ضرائب، عملیات ریاضی زیادی لازم دارد. روشهایی نظیر قانون کرامر(Cramer’s Rule)، حذفی گاوس(Gaussian Elimination)، الگوریتم توماس(Thomas Algorithm) و روش‌های مستقیم پیشرفته (Advanced-Direct Methods) جزء روش‌های حل مستقیم بشمار می‌رود.

قانون کرامر (Cramer’s Rule)

قانون کرامر یکی از ابتدایی‌ترین روشهای حل مستقیم است و شدیداً زمانبر بوده و تنها برای حل دستگاه معادلات کوچک مناسب می‌باشد. تقریباً تعداد عملیات ریاضی مورد نیاز برای حل یک دستگاه معادلات n مجهولی، !(n+1)  می‌باشد. بعنوان مثال، برای حل یک دستگاه معادله 10 مجهولی بیش از 39 میلیون عملیات ریاضی مورد نیاز است تا دستگاه معادلات مذکور حل شود. همچنین، برای حل یک دامنه محاسباتی با 11*11 گره متشکل از 81 مجهول، !82 معادل  عملیات ریاضی مورد نیاز است که انجام این محاسبات با استفاده از یک کامپیوتر با سرعت محاسباتی 100 میلیون عملیات ریاضی در ثانیه، میلیاردها میلیارد سال بطول خواهد انجامید [1]. بطور خلاصه روش کلی حل دستگاه معادلات (1) بصورت روابط اشاره شده در معادله (2) می باشد.

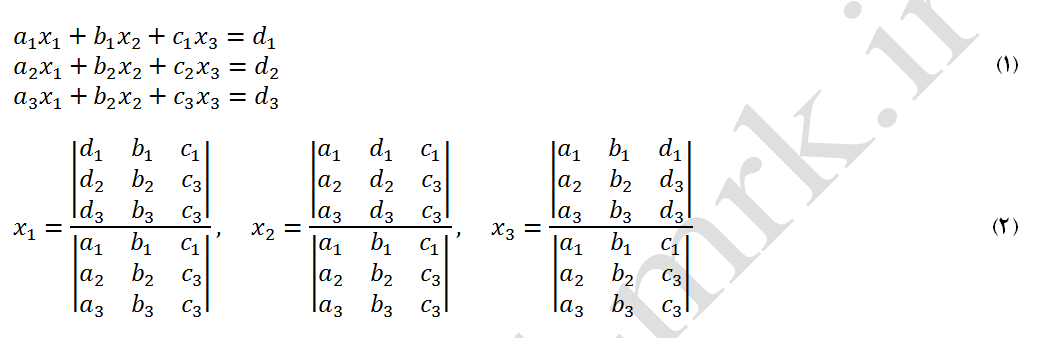
روش حذفی گوس (Gaussian Elimination Method)

روش حذفی گوس روشی بسیار مناسب و کارا برای حل ضمنی سیستم دستگاه معادلات جبری، بویژه برای دستگاه معادلات سه قطری، می‌باشد. در این روش تقریباً n³/3 عملیات ریاضی برای حل یک دستگاه n مجهولی مورد نیاز است. در مقایسه با روش کرامر، برای حل یک دامنه عددی با 11*11 گره متشکل از 81 مجهول، تنها در حدود کمتر از 180.000 عملیات ریاضی مورد نیاز بوده که به هیچ عنوان قابل مقایسه با روش کرامر نمی‌باشد [1]. باید توجه داشت که خطاهای گرد سازی در این روش قابل توجه بوده و در پاره‌ای اوقات در دستگاه معادلات با تعداد مجهولات زیاد، موجب از کار افتادن فرآیند حل می‌شود. در واقع دقت این روش به نوع سیستم دستگاه معادلات بستگی دارد. در این روش، با جابجا کردن معادلات، ماتریس ضرائب به یک ماتریس بالا مثلثی و یا پایین مثلثی تبدیل می‌شود.

برای مثال معادلات (3) را در نظر بگیرید. همانطور که اشاره شد، در روش حذفی گوس سعی بر اینست که ماتریس ضرائب دستگاه معادله (3) به یک ماتریس بالا مثلثی تبدیل گردد (معادله 4). اینکار مستلزم حذف تعدادی از مجهول‌ها و همچنین استفاده از یک سری عملیات جبری می‌باشد. با تبدیل دستگاه معادلات (3) به یک دستگاه معادلات بالا مثلثی، تنها یک مجهول در آخرین معادله و دو مجهول در معادله یکی به آخر و به ترتیب مشابه تا معادله اول ادامه یافته و دستگاه معادله (3) به دستگاه معادله بالا مثلثی (4) تبدیل می‌شود.

روش‌های حل مستقیم و تکراری

با توجه به دستگاه معادلات (4)، می‌توان پاسخ‌ها را با استفاده از طریق جایگزینی برگشتی (Back Substitution) بدست آورد. برای درک بهتر، این روش با یک مثال عددی (دستگاه معادلات 5) توضیح داده شده است. در روش حذفی گوس، عملیات ریاضی برای رسیدن به یک ماتریس بالا مثلثی با استفاده از معادلات مبنا انجام می‌شود. معمولاً در تبدیل بالا مثلثی، به ترتیب از معادله اول تا معادله ما قبل آخر بعنوان معادلات مبنا استفاده می‌شود. بهمین خاطر با در نظر گرفتن اولین معادله از دستگاه معادلات (الف-5) بعنوان معادله مبنا، مجهول u₁ از دو معادله بعدی (معادله 6) حذف می‌شود. بطور مشابه، با در نظر گرفتن معادله دوم از دستگاه معادلات (6) بعنوان معادله مبنا، u₂ از معادله آخر دستگاه معادلات (6)  حذف شده و به دستگاه معادلات (7) می‌رسیم.

                                              

با توجه به معادله سوم در دستگاه معادلات (7)، مقدار u₃=3 بدست می‌آید. در ادامه می‌توانید با استفاده از روش جایگزین برگشتی، با قرار دادن مقدار کمیت u₃ در معادله دوم از دستگاه معادلات (7)، مقدار u₂=2 و در نهایت با قرار دادن کمیتهای u₂ و u₃ در معادله اول، u₁=1 را به دست آورید.

 

 

روش توماس (Thomas Algorithm)

روش توماس در واقع حالت اصلاح شده‌ای از روش حذفی گوس است که در سال 1949 توسط توماس ارائه شد. این روش ویژه حل دستگاه معادلات سه قطری بوده که به راحتی می‌توان با استفاده از صفرهای موجود در ماتریس ضرائب، آنرا بصورت ماتریس بالا مثلثی ساده کرد. برای درک بهتر، به ماتریس سه قطری ضرائب معادله (8) توجه شود. با استفاده از روابط (9) و (10) می‌توان ماتریس معادله (8) را بصورت ماتریس بالا مثلثی تبدیل کرده و با بکارگیری روش جایگزینی برگشتی (رابطه 11) مجهولات را مشخص و در نهایت با استفاده از معادله (الف-12) معادلات را حل نمود.

سایر روش‌ها

علاوه بر روش‌های یاد شده روش‌های دیگری نیز وجود دارد سریعتر هستند. اما باید توجه داشت که هیچ یک از این روش‌ها، یک روش کلی و جامع نیست. برخی از این روش‌ها تنها برای معادلات جبری خاصی کاربرد دارد که از انواع خاصی از معادلات تفاضل محدود ناشی شده است. همچنین، اکثر این متدها تنها برای دستگاه معادلات کوچک قابل استفاده است، چرا که بدلیل افزایش خطای گرد سازی، نمی‌توان دستگاه معادلات را حل کرد.

به هر حال، انواع متعددی از روش‌های سریع و پیشرفته ارائه شده که از جمله می‌توان به روش‌های انتشار بردار خطا (Error Vector Propagation (EVP))، روشه (Roache)، کاهش زوج-فرد (Odd-Even Reduction) بونمن (Buneman) و همچنین روش تبدیل سری فوریه هاکنی (Hockney) برای حل معادله پواسون اشاره کرد. یکی دیگر از روش‌های مستقیم پیشرفته، روش ماتریس پراکنده (Spares Matrix Method ) است. البته علی رغم عمومیتش، نیازمند حافظه رایانه‌ای قابل توجهی می‌باشد و عملاً از برخی از روشهای تکراری دارای کارایی کمتری است[2].

 

حل تکراری در روش‌های حل مستقیم و تکراری

روش‌های تکراری یا همان روش‌های خلاصی (Relaxation) که سابقاً با عنوان روش‌های خلاصی باقیمانده (Residual Relaxation) نیز شناخته می‌شد به روش‌هایی گفته می‌شود که در آنها مجهولات یک دستگاه معادلات با استفاده از رویکرد سعی و خطا محاسبه می‌شود. هدف از بکارگیری روش‌های تکرار رسیدن به همگرایی سریعتر می‌باشد. چرا که هر چه همگرایی سریعتر باشد تعداد عملیات و محاسبات ریاضی کمتری مورد نیاز است و در نتیجه موجب تولید خطای همگرائی کمتری در جواب‌های نهایی می‌شود. لازم به توضیح است که هر چه بتوان از اطلاعات جدید بیشتری در روش‌های تکرار استفاده کرد، این روش‌ها سریعتر همگرا می‌شود.

بدیهی است که هر چه گسسته‌سازی معادلات حاکم در روش‌های تفاضل محدود، حجم محدود و المان محدود در فواصل کوچکتری (تعداد المانهای بیشتر و کوچکتری در یک دامنه محاسباتی) انجام شود، دستگاه معادلات و ماتریس ضرائب بطور چشمگیری بزرگ می‌شود اما در عوض چگالی ماتریس (نسبت تعداد آرایه‌های غیر صفر یک ماتریس به کل تعداد آرایه‌های آن) بطور قابل توجهی کمتر می‌شود. در چنین شرائطی استفاده از روش‌های مستقیم برای حل دستگاه معادلات بسیار بزرگ کارساز نیست. بنابراین با توجه به افزایش اندازه دستگاه معادلات و همچنین کاهش چگالی ماتریس، استفاده از روش‌های تکرار معمول‌تر و مناسب‌تر می‌باشد.

روش‌های حل مستقیم و تکراری

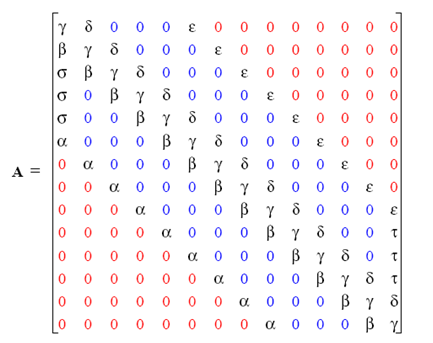
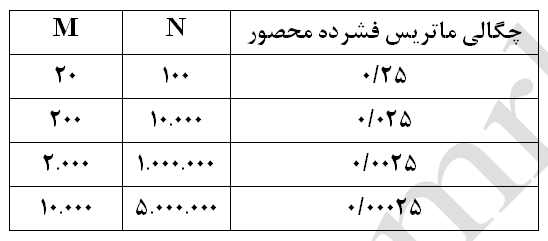
بعنوان مثالی از یک برنامه رایانه‌ای تفاضل محدود یا المان محدود، به ماتریس ضرائب نهایی A، که دارای 5 تا 10 مجهول در هر ردیف (هر ردیف این ماتریس در واقع ضرایب معادله جبری مربوط به هر گره) می‌باشد، توجه شود. برای این دستگاه معادلات، حافظه (Storage) مورد نیاز برای مد ذخیره فشرده محصور (Banded Compact Storage Mode ) برابر N*M که N اندازه ماتریس و M طول باند کل ماتریس می باشد، است. در این حالت تعداد کل آرایه‌های غیر صفر ماتریس با فرض 5 مجهول در هر ردیف معادل 5N است. همچنین چگالی ماتریس فشرده محصور (Banded Compact Matrix Density) (نسبت تعداد آرایه های غیر صفر به تعداد کل آرایه ها)، برابر با (5N/NM)=(5/M) می‌باشد. با توجه به این توضیحات، مقادیر مندرج در جدول (1) برای هر سیستم معادلات جبری صادق خواهد بود.

ماتریس ضرایب A ایجاد شده در سیستم دستگاه معادلات جبری برای 5 مجهول در هر گره محاسباتی

 

جدول-1: تغییرات چگالی ماتریس فشرده محصور و اندازه ماتریس نسبت به طول باند ماتریس (5 مجهول برای هر گره).

بطور کلی روش‌های تکرار را می‌توان به سه دسته تکرار نقطه‌ای (صریح) (Point (Explicit) Iterative Method )، خطی و بلوکی (ضمنی) (Block (Implicit) Iterative Method ) تقسیم بندی نمود. روش‌های تکرار نقطه‌ای بمراتب ساده‌تر از تکرار خطی و بلوکی بوده که در آن از یک الگوریتم ساده و مشابه برای حل معادله در تمام نقاط استفاده شده و در نهایت مجهول با جاروب کردن مداوم دامنه محاسباتی و تکرار حل بدست می‌آید. در حالیکه، در روش‌های تکرار خطی لازم است یک دستگاه معادلات برای گره‌های موجود در هر مسیر (i و j) حل شود.

در روش‌های تکرار بلوکی دامنه محاسباتی به زیر دامنه‌های محاسباتی (بلوک‌ها) تقسیم شده و در هر یک از این زیر دامنه‌ها، از روش‌های مستقیم (مانند روشهای حذفی) برای حل مسئله استفاده می‌شود. اما باید توجه داشت که یک روند تکرار برای تمام دامنه عددی و عملیات ریاضی حاکم است. در ادامه هر یک از روشهای تکرار نقطه‌ای و بلوکی توضیح داده می‌شود.

 

روش‌های تکرار نقطه‌ای

روش‌های تکرار نقطه‌ای متعددی ارائه و توسعه یافته است. مهمترین این روش‌ها شامل نقطه‌ای ژاکوبی (Point Jacobi Method)، نقطه‌ای گوس-سایدل (Gauss-Seidel) و نقطه‌ای خلاصی (Point Relaxation Methods (Successive/Systematic (Over) Relaxation – SOR)) می‌باشد که ذیلاً مورد بررسی قرار می‌گیرد.

 

روش تکرار نقطه‌ای ژاکوبی (Point Jacobi Method)

در روش تکرار نقطه‌ای ژاکوبی ابتدا در هر معادله، متغیرهای قطر اصلی براساس سایر متغیرها بصورت پارامتری حل می‌شود. سپس با یک حدس اولیه، مقدار متغیرها محاسبه می‌شود. با کمتر شدن باقیمانده متغیرها یک مقدار مشخص، مقادیر نهایی متغیرها بعنوان پاسخ سیستم در نظر گرفته می‌شود. برای مثال به دستگاه معادلات (13) توجه شود. در ادامه هر معادله متناظر با مجهول قطر اصلی ماتریس، بازنویسی شده (معادلات 14) و مقادیر متغیرها با استفاده از حدس اولیه محاسبه می شود.

با بازنویسی روابط (14)، فرم کلی روش تکرار نقطه‌ای ژاکوبی بصورت معادله (15) بدست می‌آید. روش تکرار نقطه‌ای ژاکوبی را به شکل برداری نیز می‌توان نشان داد. با فرض رابطه (16)، فرم برداری این روش بصورت معادله (17) نوشته می‌شود. در معادله (16) تمام المانهای قطری ماتریس A در ماتریس D و تمام المانهای غیر قطری ماتریس A  در ماتریس C قرار دارد. یاد آوری می‌شود که معکوس ماتریس قطری D، D^-1، به ساده‌گی و با استفاده از معکوس گرفتن از هر یک از ترم های قطر اصلی بدست می‌آید.

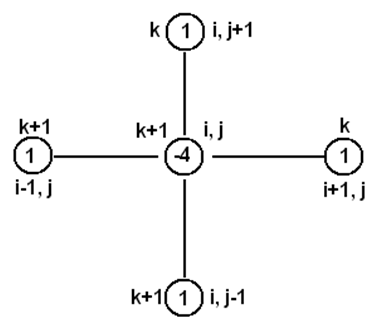
روش تکرار نقطه‌ای ژاکوبی بطور گسترده‌ای در حل مسائل CFD مورد استفاده قرار می‌گیرد. این روش مانند یک روش صریح در حل میدان جریان مطرح است. بعنوان مثالی از کاربرد روش مذکور، چگونگی گسسته‌سازی معادله لاپلاس (18) را به روش تکرار نقطه‌ای ژاکوبی در نظر بگیرید. برای حل عددی معادله (18) همواره 5 گره محاسباتی درگیر می‌باشد (شکل 2). در روش تکرار نقطه‌ای ژاکوبی، برای یافتن φ^k+1_i,j از مقادیر سایر نقاط درگیر در معادله در تکرار k، استفاده می‌شود (شکل 2).

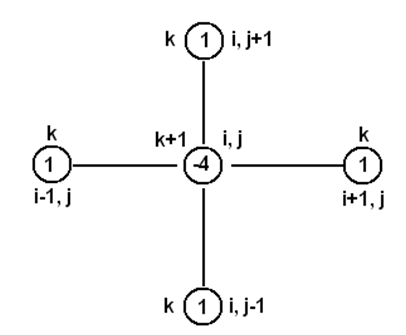
شکل-2 وضعیت مکانی و تکرار پنج گره درگیر در حل عددی معادله لاپلاس به روش نقطه‌ای ژاکوبی.

 

روش تکرار نقطه‌ای گوس-سایدل (Gauss-Seidel)

روشهای تکرار نقطه‌ای گوس-سایدل شباهت بسیاری به روشهای تکرار نقطه‌ای ژاکوبی دارد و در حقیقیت می‌توان گفت که فرم اصلاح شده روش مذکور می‌باشد. علت همگرایی سریعتر روش گوس-سایدل نسبت به روش ژاکوبی (تقریباً دو برابر سریعتر) اینست که در روش تکرار نقطه‌ای گوس-سایدل، در تکرار  از نقاطی که قبلاً در همین تکرار تصحیح شده نیز استفاده می‌شود. حل دستگاه معادلات (13) با این روش بصورت معادلات نشان داده شده در معادله (19) می‌باشد. با مقایسه رابطه (19) با معادله (14) می‌توان مشاهده نمود که در روش تکرار نقطه‌ای گوس-سایدل، بمراتب از اطلاعات جدیدتر بیشتری استفاده شده است و این مهم باعث شده که همگرایی در روش تکرار نقطه‌ای گوس-سایدل بطور قابل توجهی از روش تکرار نقطه ای ژاکوبی سریعتر باشد.

روش تکرار نقطه ای گوس-سایدل را به شکل برداری نیز می‌توان نشان داد. با توجه به رابطه (20)، فرم برداری این روش بصورت معادله (21) نوشته می‌شود. در رابطه (20) تمام المانهای قطری ماتریس A  در ماتریس D، تمام المانهای غیر قطری بالای قطر اصلی ماتریس A  در ماتریس L و تمام المانهای غیر قطری بالای قطر اصلی ماتریس A  در ماتریس U قرار دارد. در نهایت فرمولاسیون کلی روش تکرار نقطه‌ای گوس-سایدل بصورت رابطه (22) می‌باشد.

همانند روش تکرار نقطه‌ای ژاکوبی، روش تکرار نقطه‌ای گوس-سایدل نیز در ابعاد وسیعی در مسائل CFD کاربرد دارد. در رابطه (23) چگونگی گسسته‌سازی معادله لاپلاس با استفاده از روش تکرار نقطه‌ای گوس-سایدل نشان داده شده است. به تفاوت فرمولاسیون این روش با روش تکرار نقطه‌ای ژاکوبی (معادله 18) توجه شود. برای حل عددی معادله فوق همواره 5 گره محاسباتی درگیر می‌باشد. در روش تکرار نقطه‌ای گوس-سایدل، برای یافتن φ^k+1_i,j از مقادیر سایر نقاط درگیر در معادله در تکرار k+1 و k، استفاده می‌شود (شکل 3).

شکل-3: وضعیت مکانی و تکرار پنج گره درگیر در حل عددی معادله لاپلاس به روش نقطه‌ای گوس-سایدل.

لازم به توضیح است که شرط همگرایی و پایداری در روش‌های تکرار نقطه‌ای ژاکوبی و گوس-سایدل یکسان است. شرط لازم برای پایدرای روش‌های مذکور اینست که ماتریس ضرائب یک ماتریس غالب قطری باشد. بعبارت دیگر، در تمامی ماتریس‌های ضرائب لازمست که قدر مطلق مقدار متغیر قطر اصلی از قدر مطلق مجموع سایر متغیرها در آن ردیف بزرگتر و یا اینکه مساوی باشد (رابطه 24). در غیر اینصورت، باید با جابجایی ردیف‌ها این شرط را ارضاء نمود.

 

روش‌های تکرار نقطه‌ای خلاصی

روش‌های تکرار نقطه‌ای خلاصی، تصحیحات انجام شده روی متغیرهای محاسبه شده توسط روش تکرار نقطه‌ای گوس-سایدل در تکرار k+1، را بهبود می‌بخشد. این مهم با متوسط گیری وزنی از مقادیر متغیرها در تکرارهای k و k+1 انجام می‌شود (معادله 25) و در نهایت مقدار تصحیح شده متغیر در این تکرار، برای تکرار بعدی در روش گوس-سایدل مورد استفاده قرار می‌گیرد.

که در آن، x _i ^[k+1] مقدار بدست آمده از تکرار k+1 با استفاده از روش گوس-سایدل و λ ضریب خلاصی می‌باشد که باید مشخص شود. بسته به مقادیر مختلف λ، ماهیت روش تکرار نقطه‌ای بصورت‌های زیر تغییر می‌کند:

• اگر λ=0 باشد. روش مذکور به یک روش گوس-سایدل تبدیل می‌شود.
• اگر 0<λ<1 باشد. این روش یک روش زیر خلاصی (Under Relaxation) می‌باشد. در این حالت مقدار تصحیح شده نهایی هر متغیر با میانگین گیری وزنی آن متغیر در تکرار فعلی و تکرار قبلی بدست می‌آید. معمولاً از این روش برای همگرا کردن یک فرآیند غیر همگرا شونده، استفاده می‌شود. همچنین، این روش باعث افزایش سرعت همگرایی در مسائلی که همگرایی آنها دارای نوسان حول یک حل همگرا شده است، نیز می‌شود.
• اگر 1<λ<2 باشد. این روش یک روش فوق خلاصی (Over Relaxation) خواهد بود. در این حالت مقدار تصحیح شده نهایی هر متغیر با برونیابی مقادیر محاسبه شده از روش گوس-سایدل بدست می‌آید. از این روش نیز برای افزایش نرخ همگرایی استفاده می‌شود. اما باید توجه داشت که برای مقادیر 2<λ فرآیند حل دچار واگرایی خواهد شد.
• انتخاب مقدار بهینه λ کار آسانی نیست. چراکه مقدار بهینه این پارامتر به مشخصات ماتریس بستگی داشته و برای انواع مختلف مسائل دارای دامنه بهینه متفاوتی می‌باشد. معمولاً تعیین مقدار بهینه λ با استفاده از روشهای سعی و خطا امکان‌پذیر است. همچنین، در روشها و حلگرهای کوپل شده که سیستم معادلات از مشخصه‌های مختلفی برخوردار می‌باشد، مقادیر مختلفی برای λ مورد استفاده قرار می‌گیرد.

بطور گسترده‌ای از روش تکراری نقطه‌ای خلاصی نیز در مسائل CFD استفاده می‌شود. معادله (الف-26) بیانگر چگونگی گسسته‌سازی معادله لاپلاس بر اساس روش مذکور می‌باشد. برای حل عددی معادله  گسسته شده، همواره 5 گره محاسباتی درگیر می‌باشد (شکل-4).

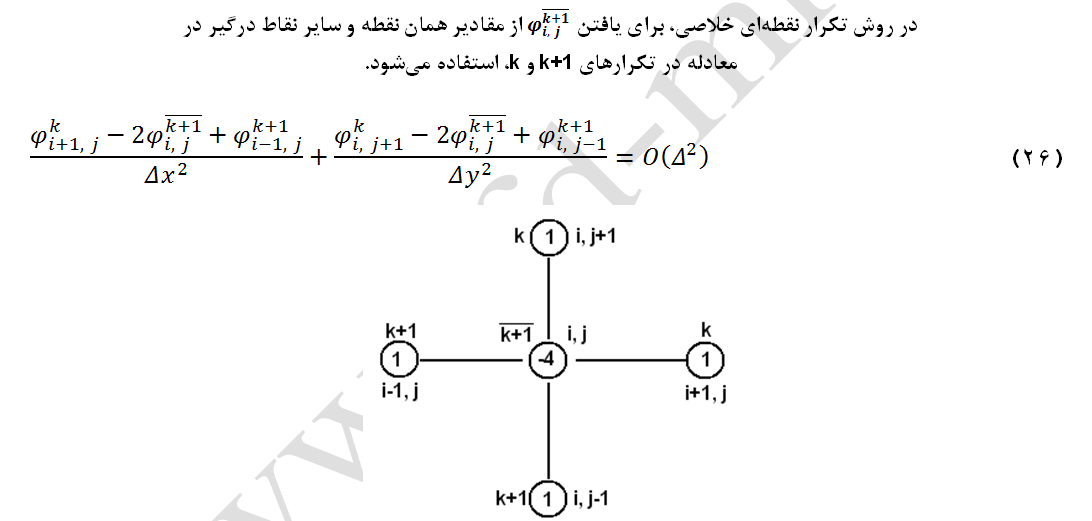
شکل-4: وضعیت مکانی و تکرار پنج گره درگیر در حل عددی معادله لاپلاس به روش نقطه‌ای خلاصی.

 

روش‌های تکرار خطی

بسته به روش مورد استفاده، در روشهای تکرار خطی بر خلاف روش های تکرار نقطه‌ای ( که همواره در هر معادله تنها یک مجهول در آخرین تکرار وجود دارد. بعنوان مثال متغیر x^k+1_i,j در معادله (15)) دو یا سه متغیر حاضر است. به عبارت دیگر، در روش تکرار نقطه‌ای حرکت نقطه به نقطه انجام می‌شود در حالیکه در روش تکرار خطی معادلات روی یک خط حل می‌شود (شکل 5). روش‌هایی نظیر روش تکرار خطی ژاکوبی، گوس-سایدل و تکرار خطی خلاصی از مهمترین روش‌های تکرار خطی بشمار می‌رود که در ادامه به جزئیات آنها پرداخته می‌شود.

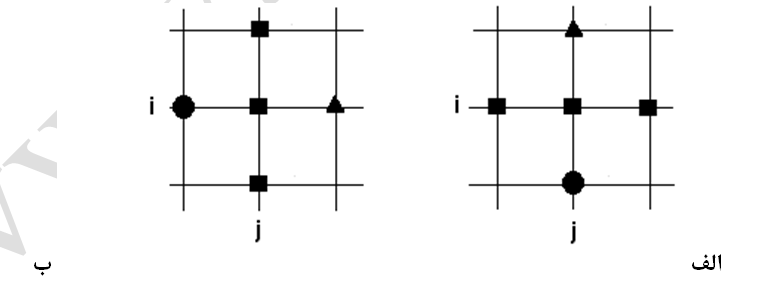
شکل-5: چگونگی درگیر بودن گره‌ها در روش تکرار خطی ژاکوبی: الف- در جهت i؛ ب- در جهت j؛

گره‌های مربع: مجهولات در تکرار k+1، گره‌های دایره: متغیر معلوم در تکرار k+1 و گره‌های مثلث: متغیر معلوم در تکرار k می‌باشد.

روش تکرار خطی ژاکوبی(Line Jacobi Method)

روش تکرار خطی ژاکوبی، یک روش حل شبیه روش ضمنی برای حل میدان عددی بشمار می‌رود که در هر معادله بیش از یک مجهول وجود دارد. بعنوان مثالی از روش تکرار، چگونگی گسسته‌سازی معادله لاپلاس با این روش را (روابط 27 و 28) در نظر بگیرید. در رابطه (27) کاربرد این روش در جهت i (شکل 6-الف) و در رابطه (28) کاربرد آن در جهت j (شکل 6-ب) در گسسته‌سازی معادله لاپلاس نشان داده شده است. همچنین نقش گره‌های درگیر و مرحله تکرار آنها در شکل (6) نشان داده شده است.

شکل-6: وضعیت مکانی و تکرار پنج گره درگیر در حل عددی معادله لاپلاس به روش تکرار خطی ژاکوبی. الف- در جهت i، ب- در جهت j.

روش تکرار خطی گوس-سایدل (Line Gauss-Seidel)

روش تکرار خطی گوس-سایدل فرم بهینه روش تکرار خطی ژاکوبی می‌باشد که همانند روش تکرار نقطه‌ای، از اطلاعات جدیدتری بهره می‌گیرد. چگونگی گسسته سازی معادله لاپلاس با این روش در معادله (29) بیان شده است. همچنین، نقش گره‌های درگیر و مرحله تکرار آنها در شکل (7) نشان داده شده است.

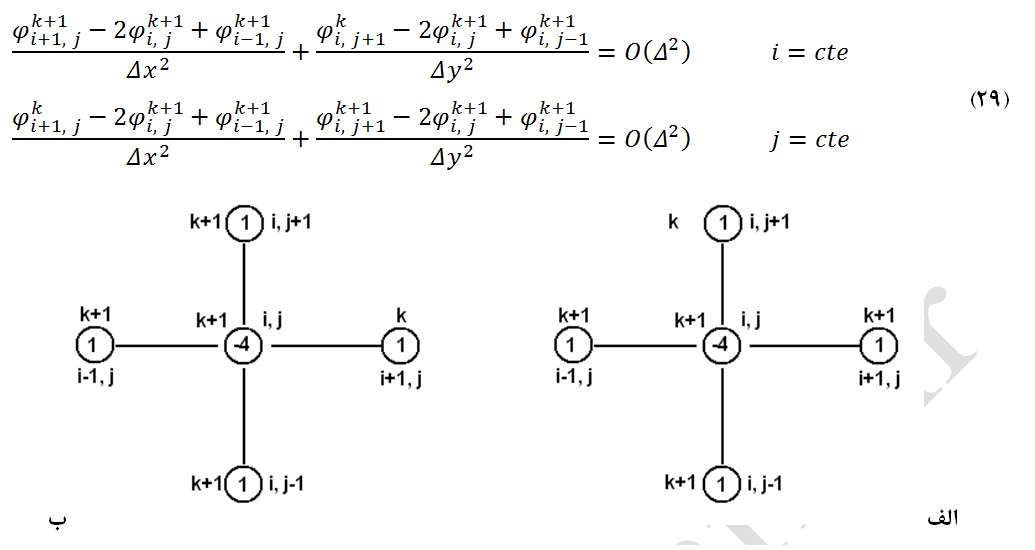
شکل-7: وضعیت مکانی و تکرار پنج گره درگیر در حل عددی معادله لاپلاس به روش تکرار خطی گوس-سایدل. الف- در جهت i، ب- در جهت j.

 

روش تکرار خطی خلاصی

همانند روش‌های تکرار نقطه‌ای خلاصی، روش‌های تکرار خطی خلاصی تصحیحات انجام شده روی متغیرهای محاسبه شده توسط روش تکرار خطی گوس-سایدل در تکرار k+1، را بهبود می‌بخشد. این مهم با متوسط گیری وزنی از مقادیر متغیرها در تکرارهای k و k+1 انجام شده و در نهایت مقدار تصحیح شده متغیر در این تکرار، برای تکرار بعدی در روش گوس-سایدل مورد استفاده قرار می‌گیرد. بعنوان مثال، به چگونگی گسسته سازی معادله لاپلاس با استفاده از این روش توجه شود (معادله 30). همچنین، نقش گره‌های درگیر و مرحله تکرار آنها در شکل (8) نشان داده شده است.

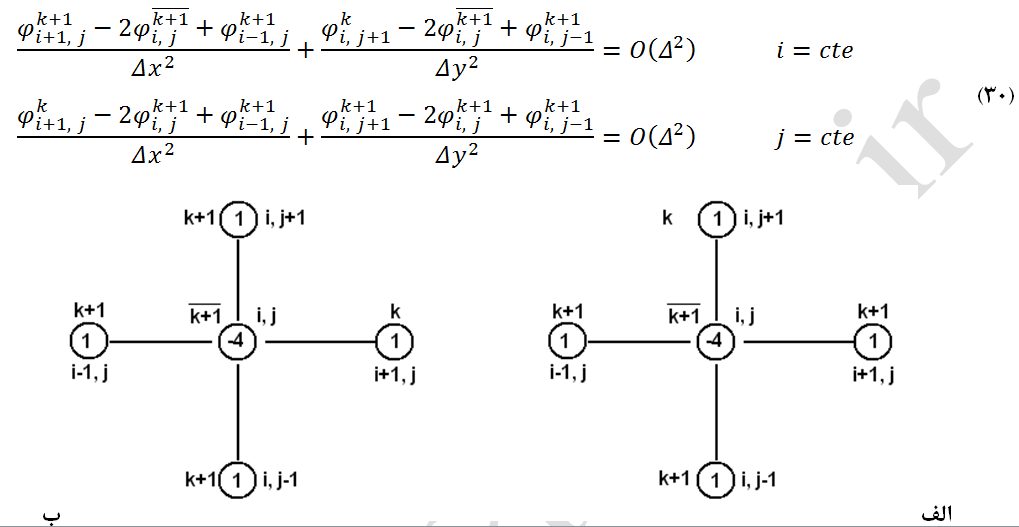
شکل-8: وضعیت مکانی و تکرار پنج گره درگیر در حل عددی معادله لاپلاس به روش تکرار خطی خلاصی. الف- در جهت i، ب- در جهت j.

 

روش‌های تکرار بلوکی

در روش تکرار بلوکی فضای دامنه عددی به زیر گروه‌هایی از گره های عددی (بلوک) تقسیم شده و برای حل هر یک از این بلوکها از روشهای حذفی (روش حل مستقیم) استفاده می‌شود، اما یک روند تکراری بر کل عملیاتهای محاسباتی حاکم است. بعبارت دیگر، روش تکرار بلوکی شامل هر دو روش حل مستقیم و تکرار می‌باشد. در شکل (9) روند کلی از چگونگی بکارگیری این روش برای حل دستگاه معادلات نشان داده شده است.

شکل-9: چگونگی حل دستگاه معادلات با استفاده از روش تکرار بلوکی.

 

روش‌های ای. دی. آی (Alternative Direction Implicit (ADI))

معمولاً می‌توان با تغییر ترتیب حرکت سطری یا ستونی نرخ همگرایی روش‌های تکرار خطی خلاصی را بهبود بخشید. بنابراین می‌توان یک حلقه کامل تکرار را با یکبار جاروب کردن تمام سطرها و یک بار جاروب کردن تمام ستونها با استفاده از روشهای تکرار خطی خلاصی، تشکیل داد. با استفاده از این روش، یک دستگاه معادلات پنج قطری به دو دستگاه معادلات سه قطری تقسیم شده و حجم حافظه مورد نیاز و پیچیدگی حل دستگاه معادلات (بویژه ماتریس ضرائب بلوکی) بطور قابل توجهی کاهش می‌یابد.

چگونگی همگرایی در روش‌های حل تکرار

همانطور که اشاره شد، در روشهای تکرار هرچه از اطلاعات جدیدتری استفاده شود، همگرایی در این روش‌ها افزایش می‌یابد. در روش‌های تکرار، روش‌های تکرار ژاکوبی از کمترین نرخ همگرایی و روش‌های خلاصی از بیشترین نرخ همگرایی برخوردار است. در شکل (10) همگرائی حل یک مسئله با استفاده از روش‌های حل مختلف تکرار نشان داده شده است. قابل توجه است که این موضوع برای هر دو روش تکرار نقطه‌ای و تکرار خطی صادق است.

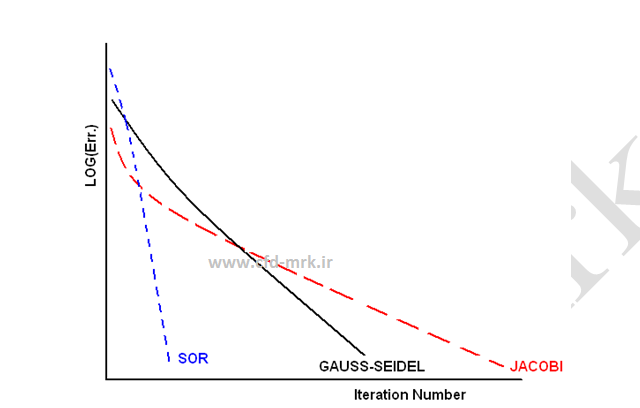
شکل-10: نرخ همگرایی در روش‌های تکرار مختلف.

روش‌های حل مستقیم و تکراری

:[1]

 C. A. J. Fletcher, “Computational Techniques for Fluid Dynamics”, Volume 2, Springer-Verlage, Second Edition, 1991

 

 

 

بازگشت

---

مطالب مرتبط

---

روش‌های تفاضل محدود در حل معادلات دیفرانسیل جزئی

برای کسب اطلاعات بیشتر با ما تماس بگیرید

دکتر محمد طیبی رهنی

محمدرضا کلیچ