روش تفاضل محدود

Finite Difference Method

روش تفاضل محدود در حل معادلات دیفرانسیل جزئی براساس محاسبه و ذخیره سازی اطلاعات روی گره‌های شبکه توسعه یافته است. اینکار با استفاده از شبکه‌بندی و اعمال معادلات حاکم روی هر یک از گره‌های شبکه انجام می‌گیرد. تقریب‌های متعددی برای گسسته‌سازی معادلات دیفرانسیل جزئی وجود دارد که مهمترین آنها تقریبهای مبتنی بر بسط سری تیلور توابع و تقریب استفاده از چند جمله‌ای‌هایی با مرتبه‌های مختلف می‌باشد. با گسسته‌سازی معادلات دیفرانسیل جزئی این معادلات به معادلات جبری تبدیل می‌شود.

لازم به توضیح است که طبیعت حل معادلات جبری بدست آمده، به خصوصیات معادلات وابسته است. بعنوان مثال، برای دستگاه معادلات تعادلی (معادلات بیضوی)، معادلات جبری حاصله باید بصورت همزمان و با مشخص بودن مقادیر مرزی، حل شود. در صورتیکه، برای معادلات سهموی می‌توان معادلات جبری مربوطه را مستقل از یکدیگر حل کرد، هرچند که حل همزمان این معادلات جبری نیز امکان‌پذیر است. روشهای مختلفی برای حل عددی معادلات دیفرانسیل جزئی توسعه یافته که می‌توان آنها را در دو دسته روش‌های صریح (Explicit) و ضمنی (Implicit) دسته بندی نمود. در طی فرآیند گسسته‌سازی مواردی نظیر پایداری (Stability)، سازگاری(Consistency) و خطاهای قطع در حل معادلات پدیدار شده که باید به آن توجه نمود. این موارد در ادامه‌ی این مبحث توضیح داده شده است.

متدهای مختلف توسعه یافته برای روش تفاضل محدود در حل معادلات دیفرانسیل جزئی

اولین گام در متد تفاضل محدود برای حل معادلات دیفرانسیل جزئی، گسسته‌سازی قلمرو فیزیکی با استفاده از شبکه‌های تفاضل محدود می‌باشد. بعنوان مثال برای حل یک معادله دیفرانسیلی که در آن u(x, y) متغیر وابسته‌ای در یک دامنه مربعی شکل (مثلاً جریان در یک حفره) می‌باشد (شکل-1)، با تولید شبکه یکنواخت روی دامنه فیزیکی u(iΔx, jΔy) جایگزین u(x, y) می‌شود. بنابراین معادلات دیفرانسیل حاکم را می‌توان بصورت معادلات جبری زیر نوشت:

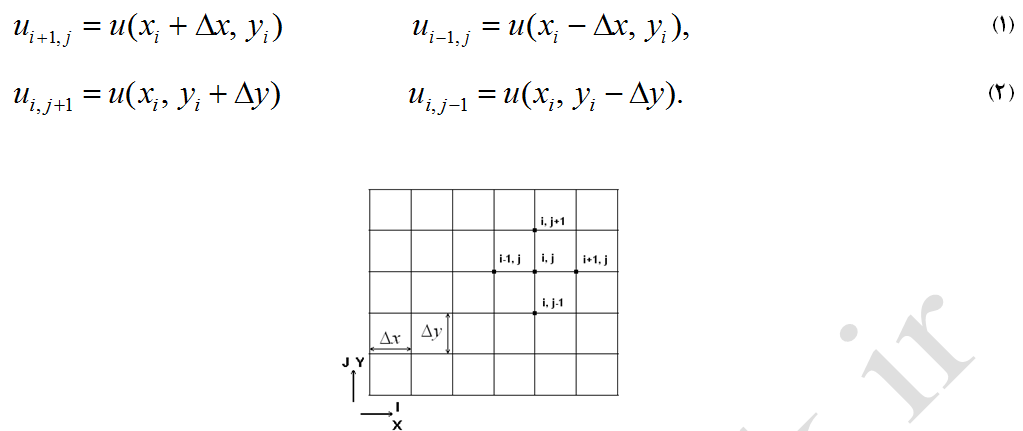
شکل -1: نمونه‌ای از شبکه تفاضل محدود

عملگرهای مهم در روش تفاضل محدود

همانطور که اشاره شد، یکی از تقریبهای تبدیل معادلات دیفرانسیل جزئی به معادلات جبری، استفاده از سری‌های تیلور می‌باشد. فرم کلی بسط سری تیلور برای یک تابع f(x) بصورت زیر است:

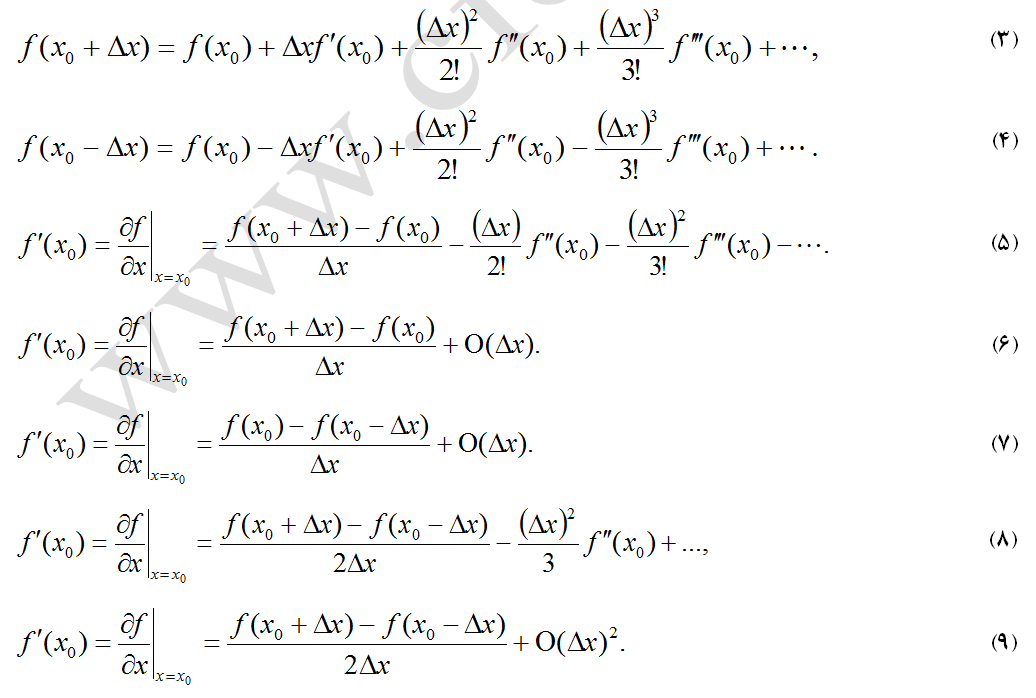
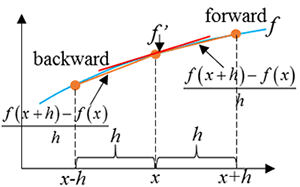
اگر رابطه (3) برای f’(x₀) حل شود، معادله (5) حاصل می‌شود. معادله (5) هم بصورت معادله (6) بازنویسی می‌شود. معادله (6) عملگر پیشرو مرتبه اول (First Order Forward Difference (First Order Upwind)) نامیده می‌شود. O(Δx) خطای قطع مرتبه اول می‌باشد. بدیهی است که با در نظر گرفتن مراتب بالاتر در گسسته‌سازی معادلات، مقدار این خطا نیز کاهش می‌یابد. از طرف دیگر با کاهش مقدار Δx، مقدار خطای قطع نیز کاهش پیدا می‌کند. بطور مشابه، برای معادله (4) هم می‌توان معادله (7) را منظور نمود. معادله (2-7) عملگر پسرو مرتبه اول (First Order Backward Difference (First Order Backwind)) نامیده می‌شود. خصوصیات رفتار خطاها در این نوع معادلات نیز همانند معادلات مرتبه اول پیشرو است.

با استفاده همزمان از دو معادله (2-3) و (2-4) می‌توان مقدار f’(x₀) را بصورت معادلات (8) یا (9) نیز محاسبه کرد. معادله (2-9)، عملگر مرکزی مرتبه اول (First Order Central Difference) نامیده می‌شود. در این روش خطاهای گسسته‌سازی از مرتبه ²(Δx) می‌باشد. در اینجا نیز هر چه مرتبه Δx بالاتر باشد، خطای حاصله کمتر می شود. از طرفی، باید تا حد ممکن به توزیع خطای یکنواخت (Uniform Error Distribution) دست یافت. توزیع خطای یکنواخت موجب همگرائی سریعتر و مشکلات پایداری کمتر می‌گردد.

عملگر پسرو کاربرد کمتری در دینامیک سیالات دارد، چرا که معمولاً اطلاعات از پایین دست به بالا دست منتقل می‌شود. برای معادلاتی که تابعی از زمان می‌باشد، همیشه تفاضل پیشرو مورد استفاده قرار می‌گیرد. توجه شود که یک عملگر ممکن است برای یک معادله سیستم پایداری ایجاد کند، اما در معادله‌ای دیگر موجب ناپایداری سیستم گردد.

بسط سری تیلور برای دیفرانسیلهای مرتبه بالاتر در روش تفاضل محدود

همانند دیفرانسیلهای مرتبه‌ اول از روشهای تفاضل پیشرو، پسرو و مرکزی برای محاسبه دیفرانسیلهای مرتبه بالاتر استفاده می‌شود. با توجه به معادلات (3) و (4)، عبارت f’’(x₀) بر اساس روشهای یاد شده بصورت زیر محاسبه می‌گردد:

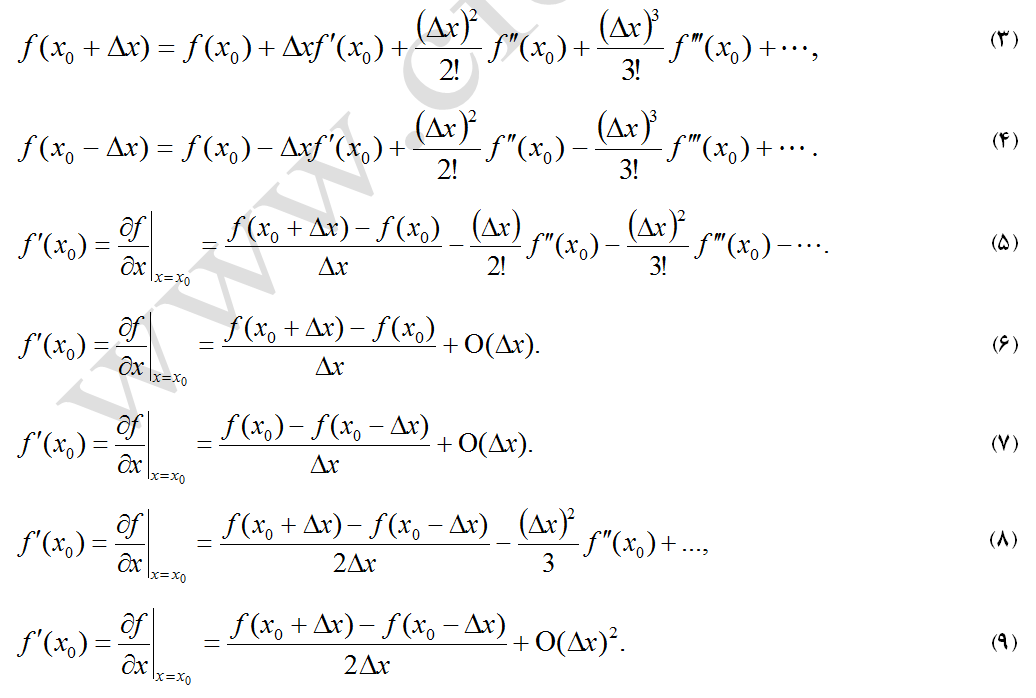
معادلات (10)، (11) و (12) به ترتیب عملگر پیشرو، عملگر پسرو و عملگر مرکزی برای محاسبه دیفرانسیل مرتبه دوم می‌باشد. جزئیات بیشتر در مرجع [1] تشریح شده است.

روشهای صریح (Explicit) و ضمنی (Implicit)

اصولاً برای حل عددی معادلات دیفرانسیل جزئی می توان معادلات را برای هر گره شبکه بطور مجزا حل کرد (روش صریح) و یا اینکه با ایجاد یک دستگاه معادلات، معادلات حاکم بر تمام گره های شبکه را بطور همزمان (روش ضمنی) حل نمود. معادلات (13) و (14) که مربوط به معادله موج مرتبه یک می‌باشد، به ترتیب نمونه‌های ساده‌ای از فرمولاسیون روشهای صریح و ضمنی می‌باشد.

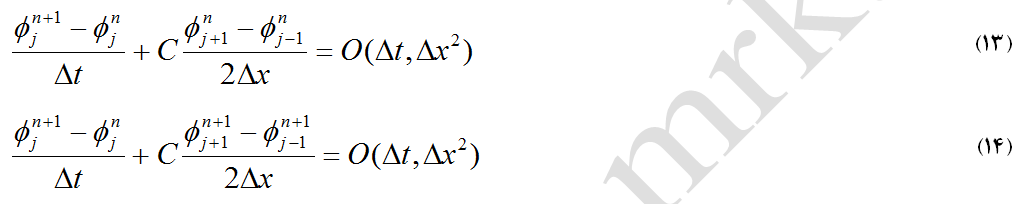
در این معادلات n مرحله زمانی (t=nΔt) و j مرحله مکانی (x=jΔx) می‌باشد. همانطور که در رابطه (13) مشخص است، الگوریتم حل برای عملیات محاسبات بسیار ساده‌تر است. تنها کمیت مجهول ϕⁿ⁺¹_j می‌باشد. اما در معادله (14) لازمست برای محاسبه کمیتهای مجهول ϕⁿ⁺¹_j-1، ϕⁿ⁺¹_j و ϕⁿ⁺¹_j+1 یک دستگاه معادله حل شود. روش صریح حل عددی معادلات بفرم کلی یک معادله خطی ax=b می‌باشد، در صورتیکه در روش ضمنی، فرم معادلات بصورت دستگاه [A]{x}=B است. بنابراین لازمست که این دستگاه معادلات در هر گام زمانی یا تکرار حل شود. روش‌های متعددی برای حل این دستگاه معادلات وجود دارد که کلاً به دو روش مستقیم (Direct Method) و روش تکرار (Iterative Method) دسته‌بندی می‌شود.

روشهای صریح تحت شرائط خاصی پایدار هستند و شروع پایداری بگونه‌ای است که Δt را به Δx ربط می‌دهد. در حالیکه روشهای ضمنی برای اکثر معادلات بخصوص برای معادلات خطی پایدار بوده و محدودیتی برای انتخاب Δt وجود ندارد. اما باید توجه داشت که انتخاب مقادیر بیش از اندازه بزرگΔt موجب از دست رفتن جزئیات (تغییرات زمانی) خواهد شد. بطور خلاصه تفاوت ماهیت روشهای صریح و ضمنی در جدول زیر درج شده است.

ویژگیهای روشهای صریح و ضمنی.

خصوصیات	روش صریح	روش ضمنی
انتشار خطا(Error Propagation)	سریع	آهسته در روشهای تفاضل محدود
پایداری	محدود	تقریباً نامحدود در روشهای تفاضل محدود
گام زمانی یا گام تکرار	کوچک	بزرگ
معکوس کردن(Inversion)	آسان	مشکل
حافظه مورد نیاز	کم	زیاد (بویژه در مسائل سه بعدی)
هزینه	بالا ناشی از زمان محاسبات	بالا ناشی از حافظه مورد نیاز
دقت	نمی توان پیش بینی نمود کدام بهتر است	نمی توان پیش بینی نمود کدام بهتر است

پایداری روشهای عددی

در حل عددی معادلات دیفرانسیل جزئی، همواره دو خطای گردکردن (ناشی از گرد کردن توسط رایانه) و خطای قطع (ناشی از گسسته‌سازی) وجود دارد. اگر در حل عددی اینگونه خطاها کنترل نشود، روند حل دچار مشکل شده و رشد خطا باعث ناپایداری حل (از نوع نوسانی و یا واگرایی) می‌گردد. داشتن شناخت کافی در مورد ماهیت این خطاها و چگونگی کنترل آنها با استفاده از آنالیز پایداری در همگرا شدن روند حل بسیار مؤثر است. پیش از پرداختن به این موضوع بهتر است مفاهیم زیر معرفی شود:

پایداری: اگر خطاهای ناشی از حل عددی معادلات رشد نکند، روش عددی استفاده شده پایدار است.
همگرایی: در صورتیکه خطای ناشی از حل عددی معادلات بسمت صفر میل کند، روش عددی استفاده شده همگرا خواهد شد.
سازگاری: اگر اندازه شبکه بسمت صفر میل کند، معادله گسسته شده بسمت معادله دیفرانسیل میل کند، آنگاه شرط سازگاری برقرار خواهد شد. هر سیستم که پایدارتر باشد، سازگاری آن نیز بیشتر خواهد بود.
نظریه هم ارزی لاکس: در صورت استفاده از معادلات دیفرانسیل جزئی برای مسائلی که شرائط اولیه بخوبی تعریف شده باشد، همگرایی این معادله دیفرانسیلی کاملاً به سازگاری و پایداری آن مربوط است.

آنالیز پایداری وُن-نیومن(Von Neumann Stability Analysis)

روشهای ون-نیومن و اغتشاش گسسته، مهمترین روشهای آنالیز پایداری برای روشهای فرمولاسیون تفاضل محدود می‌باشد. در این مطلب تنها به روش پایداری ون نیومن مورد اشاره شده است. در روش پایداری ون-نیومن، معادله مورد استفاده با سری فوریه بسط داده می‌شود. بعنوان مثال اگر معادله (15) در یک دامنه نامتنهاهی در نظر گرفته شود آن را می توان با استفاده از بسط سری فوریه بصورت رابطه (16) بازنویسی کرد:

که G ضریب رشد(Amplification Factor) یا همان مقدار دامنه در مقطع زمانی و p عدد موج (Wave Number) مربوط به x می‌باشد. باید توجه داشت که شرائط عمومی استفاده از آنالیز پایداری ون-نیومن اینست که معادله مورد مطالعه یک معادله خطی باشد. چراکه در یک معادله خطی می‌توان پاسخ‌های مختلف را به یکدیگر افزود. همچنین در معادلات خطی کافیست که تنها یک ترم سری فوریه بررسی شود. بطور کلی، شرط پایداری ون-نیومن ایجاب می‌کند که برای دامنه محدود ϕ(x, t) لازمست |G≤|1 باشد.

-[1]

K. A. Hoffman AND S.T. Chaing, “Computational Fluid Dynamics for Engineer”, Volume 1, Engineering Education System, Wichita, Kansas, 1993

بازگشت

مطالب مرتبط