تئوری مدل شکست ماداووشی

تئوری مدل شکست ماداووشی

Madabhushi Breakup Model

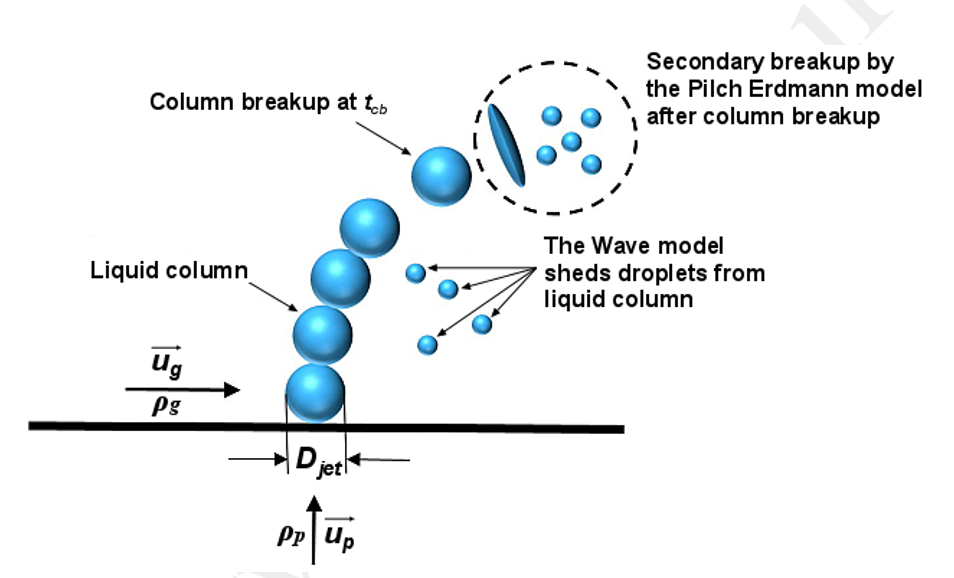
در تئوری مدل شکست ماداووشی [1]، اثرات شکست اولیه توسط مدل موجی و اثرات شکست ثانویه با استفاده از مدل پیشنهادی پیلچ (Pilch) و ادرمن (Ederman) در مرجع [2] شبیه سازی می‌شود. در شکل ابتدای صفحه مکانیزم شکست قطرات در مدل ماداووشی نشان داده شده است.

قطرات در  ابتدا از میان یک اوریفیس با قطر مشخص D_jet تزریق می‌شوند. در مرحله شکست اصلی، جت به صورت ستونی از قطرات کروی با قطرهای یکسان D₀= D_jet در نظر گرفته می‌شود. سرعت اولیه قطره u_p از سرعت جت ورودی و چگالی مایع (یا دبی جریان) محاسبه می‌شود. طی این فاز بچه قطره‌ها براساس مدل شکست موجی استاندارد تراوش می‌کنند. در ادامه، فرآیند شکست (شکست ثانویه ناشی از آشفتگی، نیروهای آئرودینامیکی و مویرگی (Capillary)) بچه‌قطره‌ها با استفاده از مدل پلیچ و ادرمن مدلسازی می‌شود.

به عبارت دیگر تا رسیدن به زمان معروف t_cd در معادله (425)، قطرات در یک ستون قرار می‌گیرند. در این رابطه u_g سرعت گاز جریان متقاطع (Cross Flow)، ρ_l چگالی سیال، ρ_g چگالی گاز و C₀ ثابت زمان شکست ستون هستند. مقدار C₀ در کارها و مقالات مختلف متفاوت است. نرم افزار فلوئنت برای این ثابت از مقدار پیشنهادی ماداووشی، C₀=3.44 استفاده می‌کند. طی این فاز ضریب درگ ثابت می‌ماند (C_D=1.48).

پس از آن که طول عمر قطرات اولیه از زمان شکست ستون، t_cb، بیشتر شد، طبق مدل پیلچ و ادرمن به قطرات کوچکتر تبدیل می‌شوند. در این مدل قطرات از کره به یک دیسک در تناوب زمانی t_def تبدیل می‌شوند (معادله 426). در رابطه (426) ^*t زمان مشخصه برای شکست است (معادله 427). U_rel سرعت نسبی بین گاز و قطره و D_parent قطر قطره محلی در ستون قطرات در زمان شکست t_cb می‌باشد. در طی تناوب زمانی تغییر شکل، نیروی درگ قطره طبق رابطه (428) تغییر می‌کند. در این معادله C_D^disk=1.2 ضریب درگ دیسک قطره است. مساحت مرجع برای تغییرات درگ نیز با استفاده از معادله (429) محاسبه می‌شود.

در نهایت نیروی درگ اعمال شده روی قطره بر اساس معادله (430) تعیین می‌شود. در این رابطه C_D ضریب درگ و A^*_P مساحت سطح مقطع (رابطه 431) هستند. با سپری شدن زمان t_def، قطره تغییر شکل داده و ضریب درگ طبق رابطه (432) ثابت باقی می‌ماند. این مهم تا زمانیکه قطره به 5 پارسل بچه قطره تبدیل شود ادامه پیدا می‌کند.

زمان کل شکست، t_b، به عدد وبر محلی وابسته است و از رابطه (433) به دست می‌آید. به خاطر انبساط اولیه اوریفیس سرعت بچه قطره، بردار u_child با استفاده از معادله (434) محاسبه می‌شود. در این معادله، بردار U_parent سرعت قطره والد و بردار u_n سرعت عمودی در صفحه عمود بر بردار سرعت والد (رابطه 435) است (شکل-1). برای هر بچه قطره زاویه جهت بردارد سرعت نرمال، α، به طور تصادفی از محدوده صفر تا  2πانتخاب می‌شود.

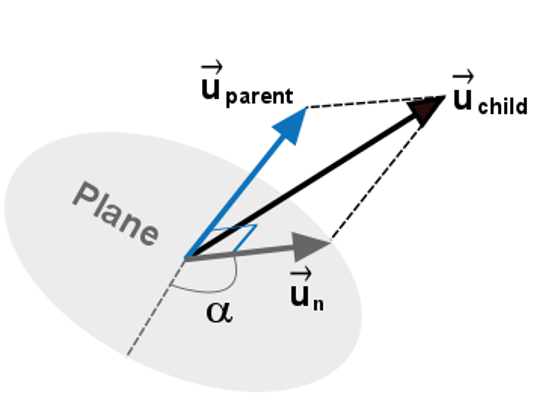
شکل-1: بردار سرعت بچه قطره در تئوری مدل شکست ماداووشی

توزیع حجمی هدف (Target Volumetric Distribution) بچه قطره‌ها پس از شکست از رابطه توزیع نرمال ریشه (Root-Normal Distribution) مشخص می‌شود (رابطه 436). در این رابطه D_0.5=1.2D_SMD و بیانگر قطرمیانگین انبوه مربوط به قطر میانگین ساتر پس از شکست (معادله 437) است.

 

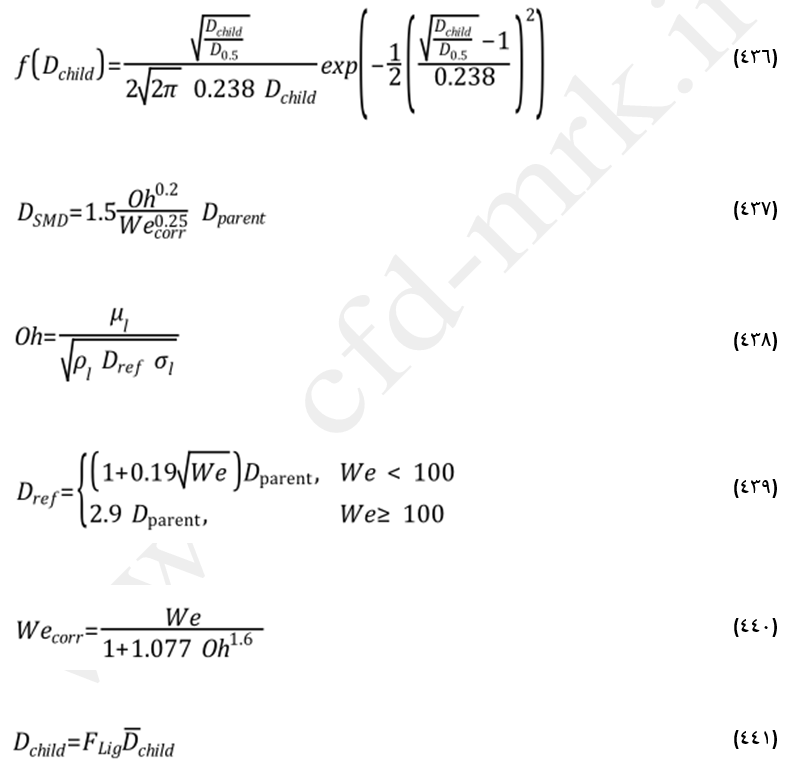
در روابط فوق:

Oh: عدد اونسرج (Ohnesorge Number) تعریف شده توسط رابطه (438)،

μ_l: لزجت قطره،

σ_l: تنش سطحی قطره،

D_ref: مساحت مرجع قطره تغییر شکل یافته (رابطه 439) و

We_corr:عدد وبر تصحیح شده برای قطرات لزجت بالا (Oh>0.1) می‌باشد که از معادله (440) محاسبه می‌شود.

توزیع قطر ماداووشی بچه قطره‌ها بعد از شکست که با توزیع نرمال استاندارد مقایسه شد در شکل (2) نشان داده شده است.

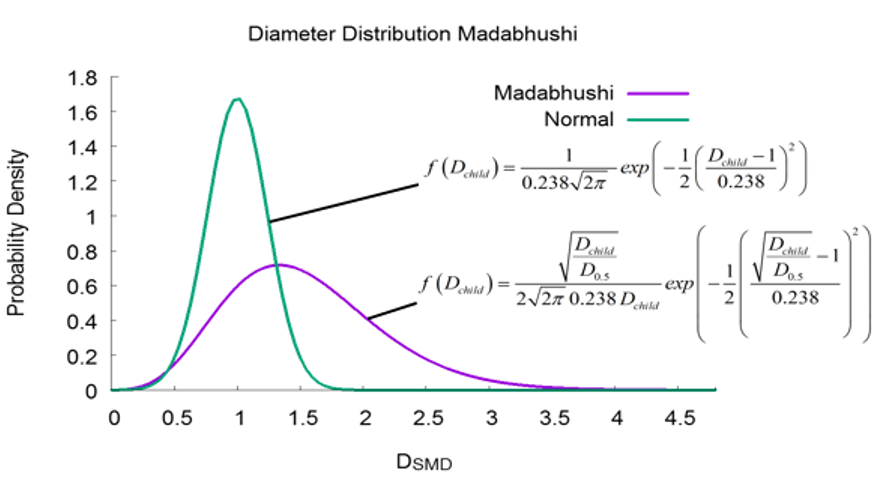
شکل-2: توزیع قطر ماداووشی در تئوری مدل شکست ماداووشی

قطراتی که پس از شکسته شدن ستون دچار شکستگی ثانویه می‌شوند، نشان دهنده تارهای (Ligaments) دنیای واقعی هستند که از هسته مایع جدا می‌شوند. تارها یا همان لیگامنت‌ها از نظر شکل متفاوت بوده که در نهایت به تارهای کوچک‌تر شکسته شده که از نظر اندازه با بچه قطره‌های اصلی تولید شده توسط مدل پیلچ و ادرمن (که قطرات والد را کروی فرض می‌کند) یکسان نیستند.

مدل پیلچ-ادرمن تمایل دارد که قطر بچه قطره‌ها را در این منطقه بیش از اندازه واقعی تخمین بزند. برای پرهیز از این خطا، قطر بچه قطره‌هایی که پس از شکسته شدن ستون دچار شکستگی ثانویه بیشتری می‌شوند، با ضریب F_lig>0 تصحیح می‌شوند تا تأثیر تارها در نظر گرفته شود (معادله 441) معادله (D^–_Child) از همان رابطه توزیع حجمی هدف بچه قطره‌ها در معادله (436) پیروی می‌کند. در این مکانیزم، بچه قطره‌ها طبق مدل پیلچ-ادرمن و بدون اعمال ضریب وزنی قطر قطرات (یعنی F_lig=1) تا زمانیکه به قدری کوچک شوند به طوریکه کشش سطح آب شروع به تشکیل قطرات جدید بکند و شکست بیشتری اتفاق نیافتد، به شکست خود ادامه می‌دهند. همین مکانیزم (یعنی F_lig=1) برای تجزیه بیشتر قطرات تراوش شده از هسته مایع توسط مدل شکست موجی اعمال می‌شود.

 

 

:[1]

R. K. Madabhushi. “A Model for Numerical Simulation of Breakup of a Liquid Jet in Crossflow”. “Atomization and Sprays”. 13. 413–424.2003

:[2]

M. Pilch and C. A. Erdman. “Discrete Element Method (DEM) Simulation and Processing of Mo/AL2O3 Granules in Fluidizing Bed”. Proc. Nat. Sci. Counc. RAOC(A). 24. 5. 394-404. 2000