جریان در قاب مرجع متحرک واحد

تئوری جریان در قاب مرجع متحرک واحد

Flow in a Moving Reference Frame

دلیل اصلی به کار گیری قاب مرجع متحرک واحد(SRF)، حل مشکل ناپایایی جریان در یک قاب مرجع ایستگاهی (اینرسیایی) با فرض پایا شدن همان جریان در یک قاب مرجع متحرک واحد می‌باشد. به عبارت دیگر ساده سازی حل جریان ناپایا به حل جریان پایا مهمترین دلیل اصلی استفاده از این روش است. برای یک قاب مرجع متحرک با ثبات ( مثلا با سرعت دورانی ثابت) می‌توان معادلات حرکت سیال را از قاب مرجع ثابت به قاب مرجع متحرک انتقال داد به طوریکه امکان حل پایای مسئله وجود داشته باشد.

باید توجه داشته باشید که می‌توانید جریان در یک قاب مرجع متحرک با سرعت دورانی ثابت را نیز به ناپایا هم شبیه سازی کنید. این مهم زمانی مورد نیاز است که شبیه سازی پدیده‌های ناپایایی همچون ریزش گردابه (Vortex Shedding) از تیغه یک فن چرخان مد نظر باشد. در واقع ناپایایی در این حالت ناشی از ناپایداری سیال (تولید گردابه) است تا اینکه به خاطر اندرکنش حرکت سیال با یک جسم یا مانع ثابت باشد.

در نرم افزار Fluent امکان تعریف حرکت قاب مرجع واحد با سرعت‌های انتقالی یا دورانی متغیر نیز وجود دارد. مجددا تاکید می‌گردد که در این روش ترم‌های شتاب اضافی مناسب به معادلات حرکت سیال اضافه می‌شوند. این گونه مسائل ذاتا به دلیل سرعت متغیر قاب ناپایا هستند.

معادلات حاکم بر قاب مرجع متحرک واحد

یک سیستم دستگاه مختصات را در نظر بگیرید که با سرعت خطی انتقال و با سرعت زاویه‌ای نسبت به یک قاب مرجع ثابت (اینرسیایی) می‌چرخد. در شکل (1) قاب‌های مرجع ثابت و متحرک نشان داده شده است. مرکز سیستم مختصات متحرک با استفاده از بردار مکان‌یابی می‌شود.

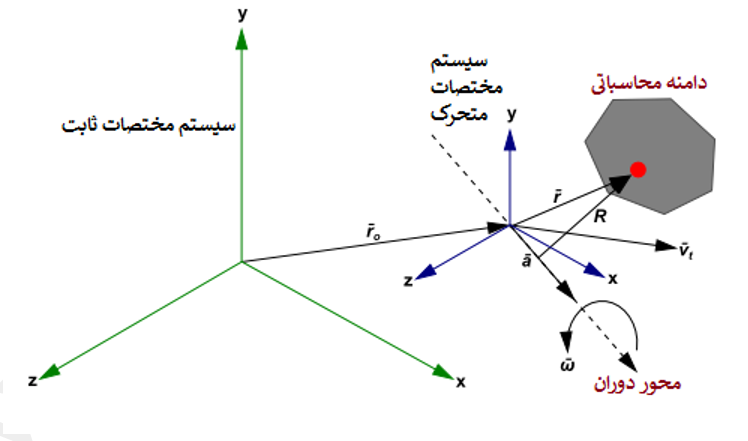
شکل-1: سیستم‌های مختصات ثابت و متحرک.

همان‌طور که در شکل بالا پیداست محور دوران توسط یک بردارد جهت یکه، ، بیان و سرعت دورانی با استفاده از معادله (1) تعریف می‌شود. دامنه محاسباتی (مسئله CFD) نیز نسبت به قاب متحرک به گونه‌ای تعریف می‌شود که هر نقطه دلخواه در دامنه محاسباتی با استفاده از بردار از مرکز مختصات قاب متحرک مکان‌یابی می‌شود. سرعت‌های سیال می‌توانند از قاب ثابت به قاب متحرک و با استفاده از معادله (2) منتقل شوند.

در معادلات بالا

Vr: سرعت نسبی (سرعتی که از قاب متحرک دیده می‌شود)،

V: سرعت مطلق (سرعتی که از قاب ثابت دیده می‌شود)،

Ur: سرعت قاب مرجع متحرک نسبت به قاب مرجع ثابت،

Vt: سرعت انتقالی قاب متحرک و

ω: سرعت دورانی قاب متحرک هستند.

باید توجه داشته باشید که Vt و ω می‌توانند توابعی از زمان باشند.

موقع حل معادلات حرکت در قاب مرجع متحرک، شتاب سیال به خاطر ترم‌های اضافی که در معادله ممنتم اضافه می‌شوند افزایش می‌یابند [1]. همچنین معادلات را می‌توان به دو روش مختلف فرموله کرد:

بیان معادلات ممنتم با استفاده از سرعت‌های نسبی به عنوان متغیر وابسته (معروف به فرمولاسیون نسبی)
بیان معادلات ممنتم با استفاده از سرعت‌های مطلق به عنوان متغیر وابسته (معروف به فرمولاسیون مطلق)

در ادامه معادلات حاکم بر هر دو روش فوق تشریح شده است. باید توجه داشت که حلگرهای فشار مبنا در نرم افزار Fluent گزینه‌ای را در اختیارتان قرار می‌دهند که می‌توانید یکی از دو روش فوق را برای استفاده در مدلسازی انتخاب کنید. در حالیکه در حلگرهای چگالی مبنا همیشه از فرمولاسیون سرعت مطلق استفاده می‌کنند.

فرمولاسیون سرعت مطلق اغلب برای کاربردهایی که در آن‌ها جریان در اغلب دامنه محاسباتی متحرک نیست (به عنوان مثال یک مسئله شبیه‌سازی جریان در یک اتاق بزرک با یک فن کوچک) ترجیح داده می‌شود. در مقابل فرمولاسیون سرعت نسبی برای مسائلی که در آن‌ها جریان در اغلب فضای محاسباتی متحرک است (به عنوان مثال یک مسئله شبیه‌سازی جریان در داخل یک مخلوط کن با یک پروانه بزرگ) مناسب‌تر می‌باشد (شکل-2).

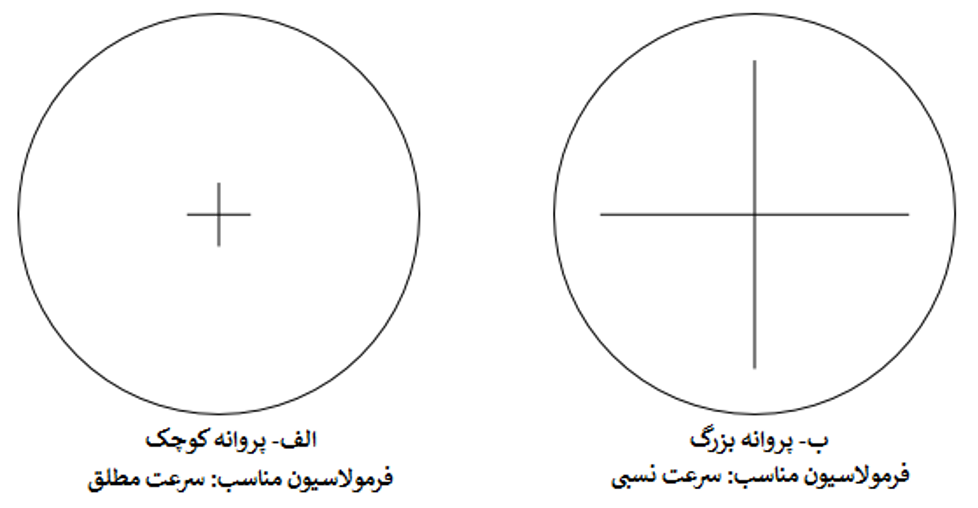
شکل-2: انتخاب فرمولاسیون سرعت‌های مطلق و یا نسبی.

نکته آخر اینکه امکان سوئیچ کردن از فرمولاسیون سرعت نسبی به سرعت مطلق و یا بر عکس آن در حین فرآیند حل ممکن نیست. برای این کار لازم است ابتدا میدان جریان با یکی از فرمولاسیون‌ها حل شده و سپس از این حل به عنوان شرایط اولیه برای فرمولاسیون دیگر استفاده نمود.

فرمولاسیون سرعت نسبی

برای فرمولاسیون نسبی، معادلات حاکم بر جریان سیال در یک قاب مرجع متحرک را می‌توان به صورت زیر نوشت

معادله بقای ممنتم از چهار ترم شتاب اضافی برخوردار است. دو ترم اول شتاب کریولیس (2ω*r) و (ω*ω*r) شتاب گریز از مرکز هستند. این ترم‌ها هم در قاب مرجع متحرک با حرک ثابت (شتاب صفر) و هم در قاب مرجع متحرک شتاب‌دار ظاهر می‌شوند. ترم‌های سوم و چهارم از تغییرات ناپایای سرعت‌های چرخشی و خطی ناشی می‌شوند. البته این ترم‌های سوم و چهارم در سرعت‌های چرخشی و یا انتقالی ثابت ناپدید می‌شوند. تنش‌ چسبندگی یا همان لزجت همانند معادله (7) محاسبه می‌شود با این تفاوت که از مشتقات سرعت نسبی استفاده می‌کند. معادله انرژی بر پایه متغیرهای انرژی داخلی نسبی (Er) و آنتالپی کل نسبی (Hr) که به عنوان روتالپی (Rothalpy) نیز شناخته می‌شود، نوشته می‌شود. این متغیرها طبق معادلات (8) و (9) تعریف می‌شوند.

فرمولاسیون سرعت مطلق

برای فرمولاسیون مطلق، معادلات حاکم بر جریان سیال در یک قاب مرجع متحرک (با سرعت ثابت) را می‌توان به صورت زیر نوشت:

در این فرمولاسیون شتاب‌های کریولیس و گریز از مرکز به صورت ترم ( ω*(V-Vt)) ساده سازی می‌شود. توجه داشته باشید که معادله ممنتم در فرمولاسیون سرعت مطلق شامل هیچ متغیری که به طور مستقیم با a و α درگیر باشد، نیست.

مشخصات نسبی حرکت قاب مرجع

درنرم افزارهایی مثل Fluent به شما اجازه داده می‌شود که قاب حرکت را نسبت به یک قاب مرجع متحرک (با حرکت انتقالی و یا چرخشی) مشخص کنید. در این حالت بردار سرعت به از طریق معاله (13) محاسبه می‌شود.

معادله (14) به عنوان تبدیل گالیله نیز شناخته می‌شود. بردارهای دوران با یک دیگر جمع می‌شوند (معادله 15) چرا که حرکت قاب مرجع را می‌توان به عنوان چرخش یک جسم جامد مشاهده کرد که در آن نرخ چرخش برای هر نقطه از دامنه ثابت است. به علاوه این مهم به فرمولاسیون دوران اجازه می‌دهد تا به عنوان یک شبه محور دوران با سرعت زاویه‌ای باشد که تبدیل‌های لحظه‌ای بی‌نهایت کوچک را توصیف کند. در این حالت هر دو نرخ چرخش تابع قانون جا به جایی هستند. توجه داشته باشید که این رویکرد هنگام برخورد با دوران‌های محدود کافی نیست. در این حالت فرمولاسیون ماتریس‌های دوران براساس زوایای اویلری ضروری است [2].

:[1]

.Y. Luo, R. I. Issa, and A. D. Gosman. “Prediction of Impeller-Induced Flows in Mixing Vessels Using Multiple Frames of Reference”. In IChemE Symposium Series.136. 549–556. 1994.

:[2]

A. V. Rao. Dynamics of Particles and Rigid Bodies. A Systematic Approach. Cambridge University Press. Cambridge, England 2006