منابع خطا در CFD
در حل عددی معادلات توسط رایانه همواره خطا وجود دارد. در دینامیک سیالات عددی علاوه بر خطاهای ناشی از حل عددی، خطاهای ناشی از مدلسازی فیزیکی و ریاضی نیز وجود دارد. با توجه داشت که موضوع یاد شده خطاها در دینامیک سیالات عددی، غیر قابل حذف است، اما میتوان آنها را بطور چشمگیری کاهش داد. مسلماً با کاهش خطاهای موجود بر دقت نتایج بدست آمده افزوده میشود. در ادامه، مهمترین منابع خطا و راهکارهای کاهش آنها توضیح داده می شود.
خطای مدلسازی هندسی
خطای مدلسازی هندسی به خطاهای ناشی از مدلسازی سطح توسط نرمافزارهای CAD گفته میشود. اگر هرگونه اختلافی در سطح بین مدل رایانه و مدل ساخته شده وجود داشته باشد منجر به خطای مدلسازی هندسی میشود. مهمترین تأثیری این خطا آنست که توزیع فشار را تحت تأثیر قرار میدهد که باعث اختلاف فاحش در مقادیر ممانها و نیروهای حاصل از نتایج CFD و تستها یا مقادیر واقعی می شود. تغییر شکل لایه مرزی و در نتیجه پروفیل سرعت در لایه مرزی و نیروی اصطکاک نیز بطور قابل توجهی متأثر از این خطا هستند. باید توجه داشت که اختلاف سطح نمونه واقعی و مدل هندسی CFD قطعاً وجود دارد. متأسفانه در اکثر موارد هماهنگی مناسبی بین گروه CFD و مدلسازهای هندسی دیده نمیشود
نکته: این خطا را نمیتوان بطور 100% حذف کرد. تنها راه برای رسیدن به خطای کمتر، استفاده از یک فایل CAD نهایی و دقیق توسط تمامی تیمهای طراحی و ساخت، به حداقل رساندن تلورانس ساخت و استفاده از شبکه مناسب سطحی میباشد.
خطای مدلسازی فیزیکی
اولین گام در حل یک مسئله واقعی، تبدیل آن به یک مدل فیزیکی میباشد که اصطلاحاً آن را مدلسازی فیزیکی گویند. همواره در انجام این مدلسازی فرضیات و ساده سازیهایی انجام میشود. بعنوان مثال جریان هوای تراکم پذیر آشفته حول یک جسم را میتوان با شرط غیر لزج بودن حل کرد و یا اینکه جریان آب در یک کانال را بدون در نظر گرفتن اثرات جاذبه شبیه سازی نمود. این ساده سازیها و فرضیات موجب بروز خطایی تحت عنوان خطای مدلسازی فیزیکی شده و در نتیجه مقادیر کمیتهای محاسبه شده نسبت به مقادیر حقیقی اختلاف خواهد داشت. بطور کلی، در بعضی موارد مدلسازی فیزیکی موجب بروز اختلافات کم و قابل چشم پوشی و در برخی حالات دارای خطاهای فاحشی بوده که لازمست در مدلسازی فیزیکی انجام شده تجدید نظر شود.
صرفنظر کردن از یک پدیده فیزیکی (همانند آشفتگی، تراکمپذیری، انتقال حرارت و …) در شبیهسازی میدان جریان منجر به تولید خطای مدلسازی فیزیکی میشود. مهمترین پدیدههای فیزیکی مطرح دینامیک سیالات عبارتند از:
تراکم پذیری،
آشفتگی،
انتقال حرارت،
دوران جریان،
پدیده چند فازی،
تغییر فاز،
واکنش شیمیایی،
پایا بودن و
…
خطای مدلسازی ریاضی
یکی از مهمترین خطاهای بحث CFD خطای مدلسازی ریاضی است. این خطا به خطای مدلهای ریاضی مختلفی که پدیدههای فیزیکی را شبیهسازی میکنند (همانند انواع مدلهای آشفتگی، مدلهای شبیهسازی جریانهای چند فازی و …)، گفته میشود. همچنین بحث دقت الگوریتمهای حل نظیرRoe و AUSM و غیره نیز در بحث خطاهای مدلسازی ریاضی مطرح میشود.
به عنوان مثال یکی از اصلیترین مشکلات شبیهسازی پدیده آشفتگی جریان است. متأسفانه روشهای RANS دقت قابل ملاحظهای در پیشگویی حقیقت آشفتگی جریان ندارد چرا که از تکنیک متوسط گیری زمانی و یا جرمی استفاده میکند. به همین خاطر قادر به تشخیص نوسانات پارامترهای جریان نبوده و بطور کلی پاسخی میانگین را ارائه میکند. استفاده از مدلهای RANS بخصوص K-E و K-W معمولاً برای جریانهایی که گرادیان فشار زیادی دارد جوابهای خیلی قابل قبولی نمیدهد. بویژه در مدل K-E که به جهت فرضیات بکار رفته در آن همواره میزان انرژی جنبشی آشفتگی را در دنبالهها، گرادیانهای فشار بالا و بخصوص جدایی جریان، را بیش از حد واقعی تخمین میزند (Over stimate) و این مهم معمولاً باعث محاسبه میزان نیروهای آئرودینامیکی (بخصوص درگ) بیش از حد واقعی خود میشود. در مقابل مدل RSM، (Turbulent Dessipation Rate) را بیش از حد واقعی تخمین میزند. ولی بطور کلی از دقت نسبتاً بهتری نسبت به سایر مدلهای آشفتگی برخوردار است. پیشگویی صحیح تنش برشی روی دیواره چالش برانگیزترین بحث در شبیهسازی جریان آشفته است.
خطای قطع (گسستهسازی)
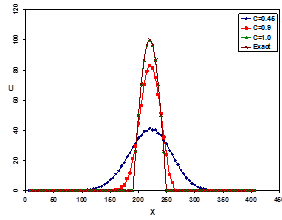
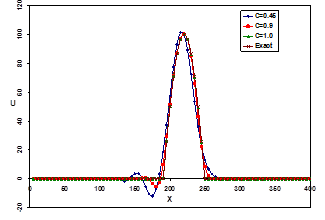
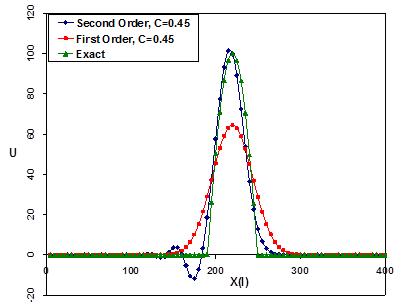
خطای گسسته سازی در واقع از تبدیل معادلات دیفرانسیل پارهای به معادلات جبری برای حل عددی تولید میشود. اگر گسستهسازس معادلات دیفرانسیل پارهای از مرتبه اول باشد خطای تولید شده خود را در دامنه پاسخها و یا نقاط پیک آنها نشان میدهد (مقدار پیک پارامترها را نمیتواند پیش بینی کند). در صورتیکه گسسته سازی معادلات از مرتبه دوم باشد خطای تولید شده از نوع نوسانی خواهد بود.
الف
ب
ج
حل معادله موج با گسسته سازی مرتبه اول (الف) و مرتبه دوم (ب) و مقایسه بین مرتبه اول و دوم با عدد کورانت 0.45 (ج)
نکته دیگری که در خطای گسستهسازی از اهمیت فوق العادهای برخوردار است کیفیت شبکه میباشد. در شکلهای بالا به ازای عدد کورانت c=1.0 تفاوتی بین دقت در هر دو مرتبه اول و دوم وجود ندارد. در واقع کیفیت شبکه تأثیر مستقیم روی عدد کورانت و خطای گسستهسازی دارد.
تراکم مناسب شبکه و استفاده از گسستهسازی مرتبههای بالاتر در کاهش خطای گسستهسازی بسیار تأثیر گذار است. بخصوص در شبکههای بیسازمان توصیه میشود که از گسستهسازی مرتبههای بالاتر استفاده شود. لازم به توضیح است برای جریانها و هندسههای پیچیده هیچگاه نمیتوان خطای گسستهسازی را بطور کامل از بین برد و تنها میتوان آن را کاهش داد.
خطای ماشین
خطای ماشین یا همان خطای گرد کردن خطایی غیر قابل اجتناب است. برای کاهش این خطا لازم است از حلگر دقت مضاعف (Double Precision) استفاده شود که در شبیهسازی انجام شده لحاظ گردید.
خطای همگرایی (خطای تکرار)
خطای همگرایی به خطایی گفته می شود که در طی تکرارهای مربوط به در روشهای حل سعی و خطا پدید میآید. این امکان وجود دارد که در تکرارهای زیاد، خطاهای مختلف پدیدار شده در هر تکرار انباشته شده و در نهایت خطای نهایی قابل توجهی بوجود آید. برای کاهش این خطا میتوان از شبکه، گسستهسازی و الگوریتمهای حل بهینه و مناسبتر جهت کاهش تعداد تکرار استفاده نمود.
CFD هیچگاه روشی ایدهال نبوده بلکه ترکیبی بهینه است از روشهای موجود. به عنوان مثال ممکن است با تعداد المانهای شبکه خطای گسستهسازی کم شود اما در عوض موجب افزایش خطای ماشین و جمع شدن آنها میشود. این خطاها با افزایش تکرارها رشد پیدا میکنند که اصطلاحاً به آن خطای تکرار میگویند.
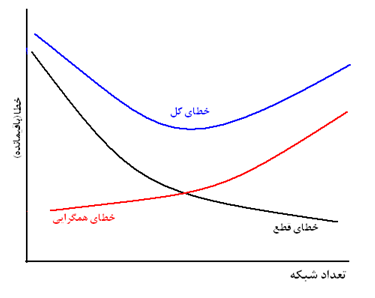
روند رشد خطا نسبت به تعداد درجات آزادی (تعداد گرهها یا المانهای شبکه).
.
خطای کاربر
این خطا در واقع ناشی از اشتباههای کاربر در تعیین مقادیر مختلف و یا برنامه نویسی میباشد که از مهمترین آنها میتوان به موارد زیر اشاره کرد:
شرائط مرزی
شرائط اولیه
مقادیر مرجع (Reference Value) نظیر مساحت مرجع، طول مرجع و …
تصویر نیروها و ممانها به محورهای متناسب با جهت جریان.
خطای نگارشی در برنامه نویسی
خطای منطقی در برنامه نویسی (به عنوان مثال به جای علامت ضرب علامت جمع در یک خط از برنامه نویسی نوشته شود)
خطای مقیاسهای کوچک (Subtle Error)
این خطا در دامنه اعداد بسیار کوچکتر از 1 ظاهر میشود. ممکن است این خطا بطور مستقیم و یا بطور غیر مستقیم در نتایج نهایی تأثیرگذار باشد. اثر مستقیم این خطا بدین صورت است که ممکن است در برخی مسائل حقیقی مقدار کمیت مورد محاسبه بسیار کوچک (مثلاً از مرتبه ) باشد بطوریکه این مقدار از مرتبه نمایش ماشین (که معمولاً می باشد) نیز کوچکتر باشد. آنگاه نتایج بدست آمده دارای خطای فاحشی بوده و به هیچ عنوان قابل اعتماد نمیباشد. بعنوان مثالی برای اثر غیر مستقیم این خطا، توزیع فشار محاسبه شده روی مدل تفاوت اندکی با مقدار واقعی داشته باشد اما در محاسبه ممان ها بویژه ممانهای غلتشی و پیچشی این خطاها با یکدیگر جمع شده و خطای قابل توجهی نسبت به تست های تونل باد ایجاد میکند.
