شبکه بندی باسازمان
Structured Grid (Mesh) Generation
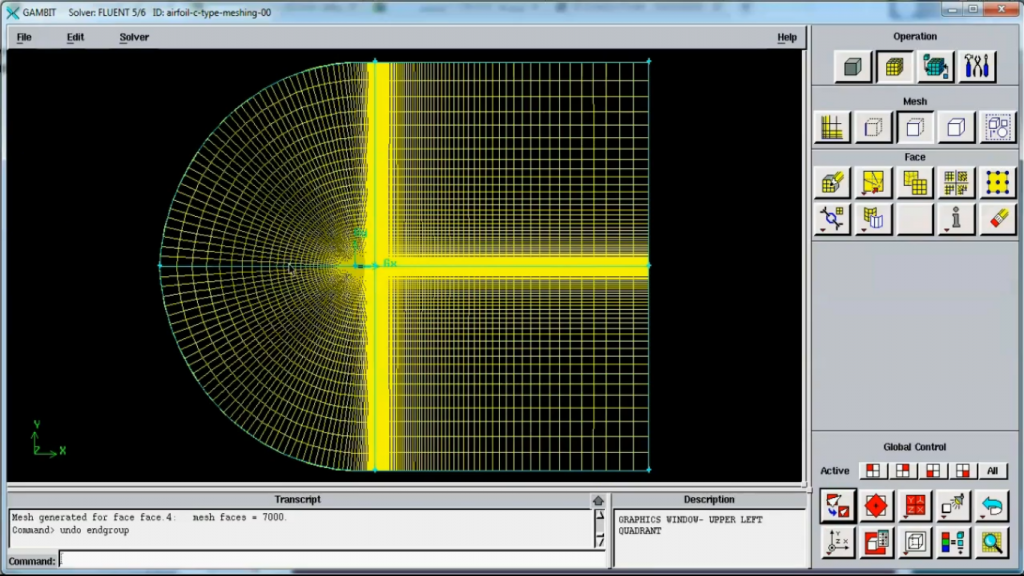
قبل از هر صحبتی، یک کلام و ختم کلام اینکه اساس شبکه بندی باسازمان بر تعریف ماتریسی سلولها (یا همان المانها) استوار است. همانطور که در اینجا توضیح داده شده شبکه باسازمان شبکهای است که در آن المانها (سلولها) از چینش منظم و سازمان یافتهای برخوردار هستند. این مهم تنها با تعریف سلولها بصورت آرایههای i,j در دو بعد و i,j,k در سه بعد امکان پذیر است. برای آشنایی با خصوصیات، مزایا و معایب شبکههای باسازمان به این صفحه مراجعه کنید.
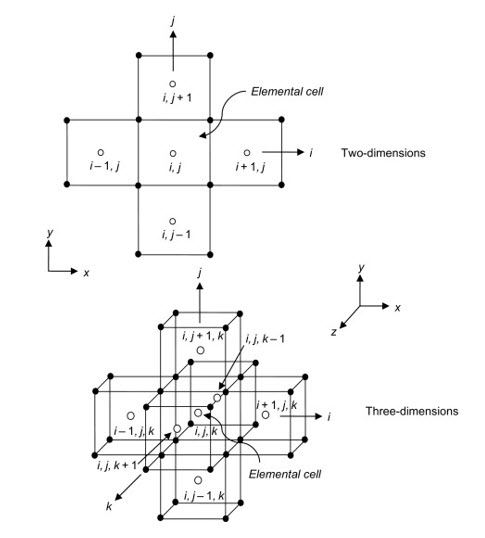
شکل-1: نامگذاری شبکههای باسازمان دو بعدی و سه بعدی.
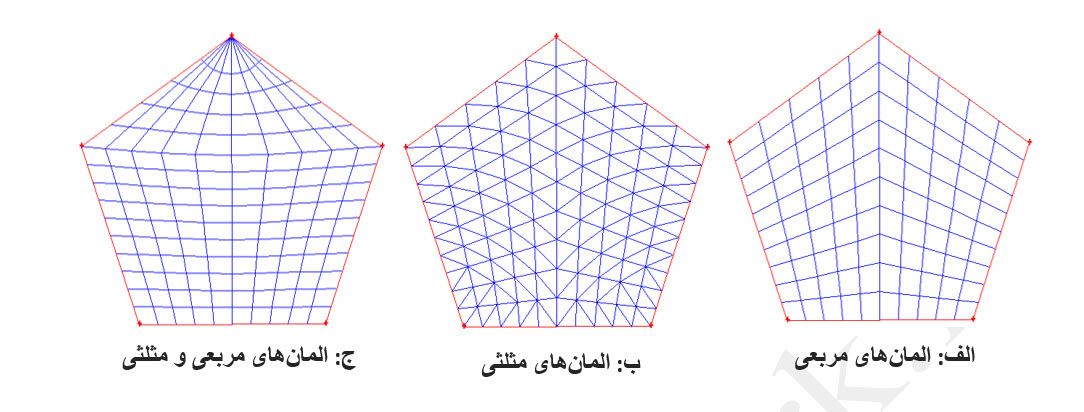
شبکههای باسازمان دو بعدی ممکن است از المانهای چهارضلعی (Quad)، سه ضلعی (Tri) و یا ترکیبی از هر دو برخوردار باشند (شکل-2). المانهای چهار ضلعی به طور مستقیم و با استفاده از ارتباط نودهای محاسباتی (نقاط توزیع شده روی سطح) تولید میشوند. در مقابل، روش مشخصی برای تولید المانهای سه ضلعی به طور مستقیم وجود ندارد (شکل-3) بلکه این المانها با تقسیم المانهای چهار ضلعی به دو مثلث پدید میآیند.
شکل-2: انواع شبکههای باسازمان دو بعدی با المانهای مختلف.
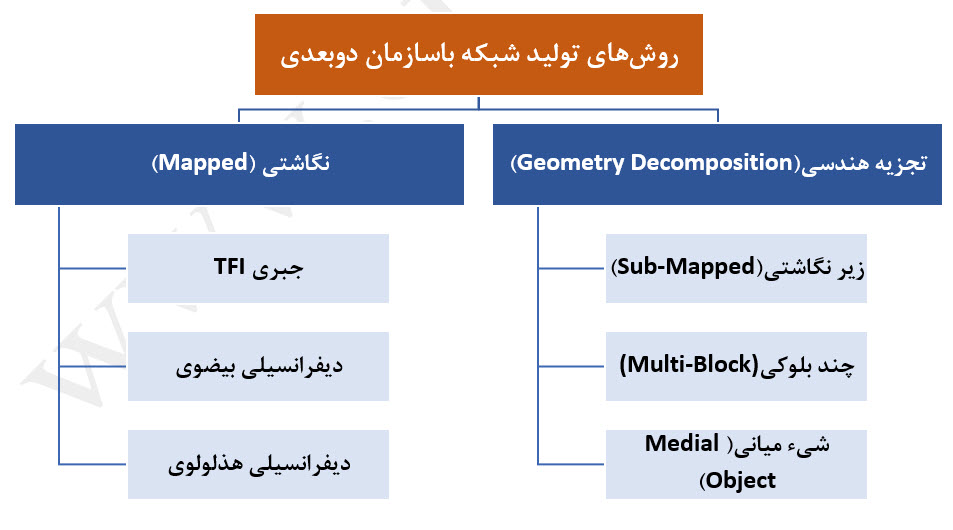
در تولید شبکه باسازمان دو بعدی و سه بعدی دو رویکرد اصلی مطرح است. رویکرد اول شبکه بندی باسازمان نگاشتی (Mapped Meshing) است که برای هندسههای ساده استفاده میشود. راهکار دوم که برای هندسههای پیچیده مناسب است مش بندی باسازمان با استفاده از تجزیه هندسی (Geometry Decomposition) میباشد (شکل-3).
شکل-3: روشهای تولید شبکه باسازمان دو بعدی و سه بعدی.
فعالیت اصلی در شبکه بندی باسازمان نگاشتی توزیع نقاط روی سطح میباشد. در این رویکرد نقاط میتوانند با استفاده از روابط جبری یا دیفرانسیلی توزیع شوند.
روشهای جبری از میانیابی ساده (بسته به رابطه انتخاب شده) موقعیت نودهای مرزی، برای توزیع نودهای داخلی استفاده میکند. روشهای دیفرانسیلی بیضوی حتما به یک توزیع اولیه نقاط (که معمولا از طریق روشهای جبری ایجا میشود) نیاز دارند تا شبکه را از نقطه نظر معیارهایی همچون هموارسازی (Smoothing)، تعامد (Orthogonality)، تراکم و غیره بهبود ببخشند. در متد دیفرانسیلی هذلولوی رشد شبکه از یک مرز به سمت بیرون صورت میپذیرد. در واقع روابط هذلولوی برای تولید شبکه حول اجسام که مرز خارجی مشخص ندارند (مثل تولید شبکه اطراف یک مخروط) بسیار مناسب هستند.
شبکه بندی باسازمان بر اساس تجزیه هندسی به این صورت است که هندسههای پیچیده در قالب اشکال چهار لبهای (هر لبه ممکن است از یک یا چند ضلع تشکیل شود) و از روش نگاشتی شبکه بندی شوند. صفحات پیچیده میتوانند صراحتا به زیر صفحات 4 لبهای تجزیه شوند (روش چند بلوکی (Multi-Block)) یا اینکه به طور غیر مستقیم و با استفاده از تعریف گرههای مرزی با عناوین مشخص و معروف به روش زیر-نگاشتی (Sub-Mapped) به سطوح 4 لبهای تشکیل شوند.
در مورد این دو روش مفصل صحبت میکنیم. روش شیئ میانی که با روش محور میانی (Medial Axis) هم شناخته میشود زمانی مورد استفاده قرار میگیرد که یک حفره در داخل مدل هندسی وجود داشته باشد. این روش با تجزیه اولیه هندسی و توسعه آن شرایط برای تولید شبکه باسازمان با المانهای چهار ضلعی را فراهم میکند. در ادامه هر یک از روشهای فوق به تفصیل تشریح شده است.
شبکه بندی باسازمان نگاشتی (Mapped)
به شخصه هر وقت صحبت از شبکه باسازمان نگاشتی میشود به یاد حل معادلات دیفرانسیل جزئی با تبدیل قلمرو فیزیکی به یک دامنه محاسباتی میافتیم که در آن علاوه بر تولید شبکه در یک دامنه مستطیل شکل (دامنه محاسباتی ) و نگاشت آن روی هندسه واقعی (قلمرو فیزیکی) همراه با فرمولهای طولانی و متریکها و ژاکوبینهای تبدیل برای نگاشت این معادلات در دامنه محاسباتی سرو کار داشتیم.
درونیابی نامتنهای (Transfinite Interpolation) اصلی ترین روش تولید شبکههای با سازمان مناسب برای حل عددی معادلات دیفرانسیل جزئی است. به هر حال هر چند در اینجا قصد ندارم راجع به نگاشت شبکه از دامنه مستطیل شکل به هندسه واقعی و مپ کردن معادلات دیفرانسیل جزئی حاکم بر جریان در فضای محاسباتی صحبت کنم اما حتمن روش TFI را به شما معرفی میکنم. در واقع هدفم از نگارش این بخش معرفی مرحله اول یعنی روشهای تولید شبکه در هندسه واقعی میباشد.
همانطور که از اسمش پیداست شبکه بندی باسازمان نگاشتی از نگاشت یک صفحه به یک صفحه مستطیل شکل (چهار لبهای) بهره میبرد. به عبارت دیگر در این روش ابتدا سعی میشود که صفحه دو بعدی معادل یک سطح 4 لبهای فرض شده (البته بدون تغییر هندسه) و سپس نقاط روی سطح به وسیله متدهای جبری و دیفرانسیلی توزیع و یا تصحیح گردد. در این روش دو موضع اصلی زیر مطرح است:
- شکل هندسی دوبعدی حتما باید 4 لبه داشته باشد (شکل-4).
- یک تناظر یک به یک بین نقاط مرزی لبههای رو به رو با هم بر قرار باشد (شکل-4).
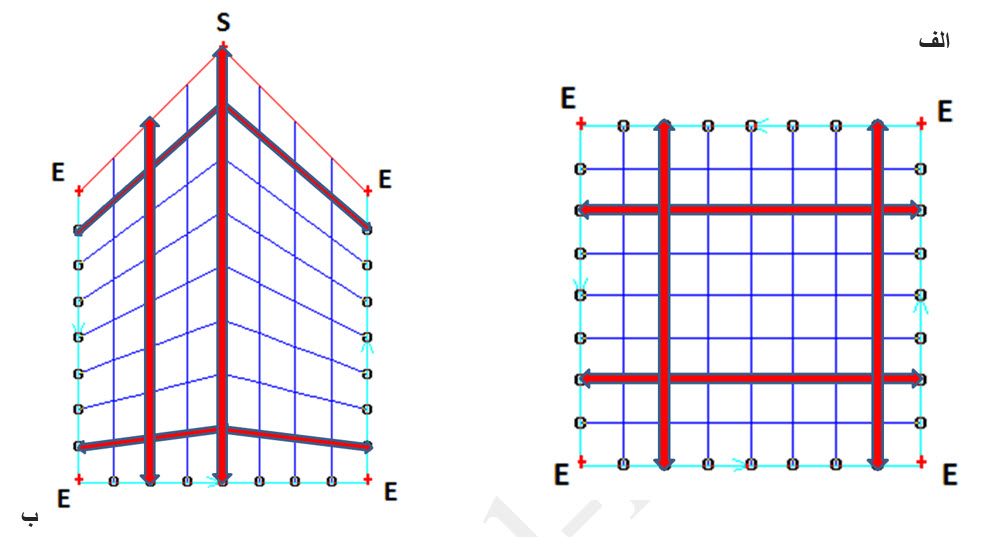
شکل-4 تولید شبکه باسازمان بر اساس دو اصل شکل هندسی 4 لبهای و تناظر یک به یک نقاط شبکه مرزی بین لبههای رو به روی هم.
وقتی میگوییم برای شبکه باسازمان نگاشتی سطح حتمن باید از 4 لبه تشکیل شده باشد یعنی اینکه شکل هندسی حتما باید دارای 4 گره انتهایی باشد که تنها با یک المان در ارتباط هستند. در شکل بالا این گرهها با حرف E، مخفف End، نشان داده شدهاند. بنابراین هر لبه (متشکل از یک یا چند ضلع) حتمن باید بین دو گره End قرار گیرد و گرههای میانی (گره مرزی بین دو ضلع لبه بالایی شکل-4:ب) باید تنها جزء دو المان همسایه باشند. این گرههای میانی با حرف S، مخفف Side، تعریف میشوند.
تناظر یک به یک نقاط روی لبههای رو به رو به این معنی است که تعداد نقاط (المانهای) لبههای رو به رو با هم برابر است. بنابراین اگر دو لبه رو به رو از تعداد اضلاع متفاوتی تشکیل شده باشند لازمست مجموع تعداد المانهای اضلاع هر لبه با مجموع المانهای اضلاع لبه رو به رو با هم برابر باشد (شکل-4). بدیهی است که تراکم نودهای محاسباتی لبهها روی تراکم المانهای سطح تأثیر مستقیم دارد.
همانطور که گفته شد از سه روش معروف توزیع نقاط نودهای محاسباتی برای شبکه بندی باسازمان نگاشتی استفاده میشود. روش اول که از میانیابی مکانهای نودهای محاسباتی برای توزیع نقاط بهره میبرد به روش (Transfinite interpolation) یا همان روش TFI معروف است. روش دوم از توابع دیفرانسیل بیضوی استفاده میکند که صرفا برای بهینهسازی موقعیت نودهای محاسباتی اولیه تولید شده (معمولا با استفاده از روشهای TFI) روی سطح بر اساس معیارهای گونگاون به کار میرود.
در نهایت روش سوم به معادلات جزئی هذلولوی اختصاص دارد که با برونیابی نقاط شبکه را توزیع میکند. در ادامه هر یک از این روشها معرفی شده است.
مهمترین روشهای تولید شبکه باسازمان نگاشتی (Mapped) عبارتند از:
1- شبکه بندی باسازمان جبری (TFI)
2- شبکه بندی باسازمان دیفرانسیلی بیضوی
3- شبکه بندی باسازمان دیفرانسیلی هذلولوی
حل یک مثال: تولید شبکه باسازمان جبری (TFI) و دیفرانسیل بیضوی حول ایرفویل NACA0012
شبکه بندی باسازمان با تجزیه هندسی(Geometry Decomposition)
شبکه بندی باسازمان با استفاده از تجزیه هندسی یکی از پرکاربردترین تکنیکهای مش بندی در شبیه سازی جریان سیالات به شمار میرود. در این نوع شبکه بندی سه روش اصلی برای مسائل دو بعدی وجود دارد که عبارتند از روشهای:
1- شبکه بندی-چندبلوکی (Multi Block Grid Generation)
2- شبکه بندی زیر-نگاشتی (Sub-Mapped Grid Generation)
3- شبکه بندی شیء میانی (Medial Object Grid Generation)
اساسا تولید شبکه باسازمان چند بلوکی برای شبکهبندی باسازمان هندسههای پیچیده اینجام میشود. برای مسائل بسیار پیچیده مثل شبکه بندی حول هواپیما، داخل توربینهای گازی و غیره دیگر روابط ریاضی به تنهایی کافی نیستند بلکه خلاقیت، هوشمندی و هنر کاربران هم به شدت در کیفیت شبکه تولید شده نقش دارند. مبنای شبکه چند بلوکی بر تقسیم فضای محاسباتی به بخشهایی که بتوان در آنها شبکههای مناسب نگاشتی (Mapped Mesh) تولید کرد و ارتباط مناسبی بین این بخشها ایجاد نمود استوار است. پس از مشخصشدن بخشها هر یک از آنها با یکی از روشهای جبری TFI و یا دیفرانسیلی شبکه بندی میشوند. این کار آنقدر زمانبر و کسل کننده است که ممکن است تا 75% از کل فعالیتهای شبیه سازی جریان با استفاده از نرم افزارهای تجاری را به خود اختصاص دهد.
شبکه زیر نگاشتی (Sub-Mapped Mesh) برای هندسههای نسبتا سادهتر بکار گرفته میشود. این روش زمانی در دو بعد کاربرد دارد که بتوان دامنه محاسباتی را یک معادل یک چهار ضلعی در نظر گرفت که دارای چهار گره (Vertex) انتهایی (End) باشد. نکته مهم در این روش تعریف مناسب گرهها است که کاملا به شکل هندسی مسئله مرتبط است. پس از تعریف مناسب گرهها با دامنه محاسباتی استفاده از روشهای جبری TFI و یا دیفرانسیلی شبکه بندی میشود.
تولید شبکه به روش شی داخلی یا همان شیئ میانی (Medial Object) که به روش تبدیل محور داخلی (Medial Axis Transform: MAT) هم معروف است. الگوریتمهای مبتنی بر تبدیل محور میانی (MAT) برای تجزیه دامنه توسعه یافته است که عمدتا از روشهای مبتنی بر ورونی (Voroni) استفاده میکنند. برای کسب اطلاعات بیشتر به اینجا مراجعه نمایید.
ادامه دارد…
http://www.ijrame.com/wp-content/uploads/2019/03/V5i503.pdf
بازگشت
مطالب مرتبط
شبکه بندی بیسازمان دو بعدی
برای کسب اطلاعات بیشتر با ما تماس بگیرید
محمدرضا کلیچ