حل معادلات بیضوی به روش تفاضل محدود

حل معادلات بیضوی به روش تفاضل محدود

Solving Elliptic PDEs Using FDM

 

حل معادلات بیضوی به روش تفاضل محدود موضوع این پست است. صبق مطالب مندرج در در پست روش‌های تفاضل محدود و همچنین، با توجه به شکل (1)، تابع u(x,y) به فرمهای زیر گسسته‌سازی می‌شود:

با ترکیب روابط فوق در حالتهای مختلف می‌توان عملگرهای مختلفی بدست آورد. متداول‌ترین روش موجود برای حل عددی معادله لاپلاس به روش تفاضل محدود، فرمول پنچ نقطه (Five Point Formula ) است که برای نخستین بار توسط رانگ در سال 1908 ارائه گردید [1]. در فرمول پنج نقطه به نقطه علاوه بر گره محاسباتی مورد بحث (گره i, j)، چهار گره دیگر که همسایه‌های گره مذکور هستند، نیز در محاسبات شرکت می‌کنند (شکل1).

در ارتباط با این موضوع، معادله لاپلاس (معادله 1) براساس تفاضل مرکزی با دقت مرتبه دوم گسسته‌سازی شده است. فرم گسسته‌شده معادله لاپلاس بصورت (معادله 13) است. بنابراین، گره‌های شبکه‌ متناظر با معادله (13) همانند شکل (1) می‌باشد.

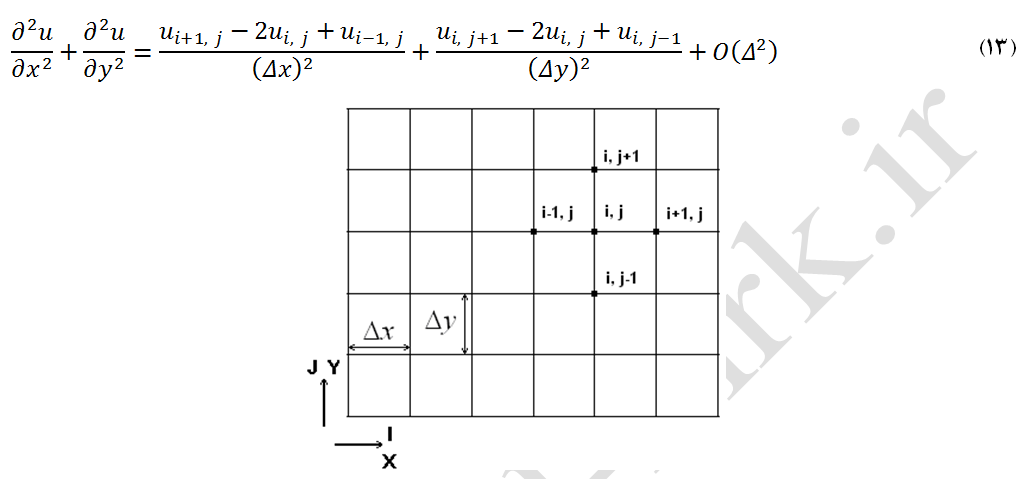
شکل-1: گره‌های درگیر شبکه در روش فرمول پنج نقطه.

 لازم به توضیح است که گسسته‌سازی معادله لاپلاس با دقت مرتبه بالاتر نیز امکان پذیر است. در این حالت از گسسته‌سازی تفاضل مرکزی با دقت مرتبه چهارم استفاده می‌شود که به فرمول نه (9) نقطه معروف است (شکل2). بنابراین، فرم گسسته‌شده معادله لاپلاس با دقت مرتبه چهارم بصورت معادله (14) می‌باشد. گره‌های شبکه متناظر با فرمول نه‌ نقطه به نقطه نیز همانند شکل (2) است.

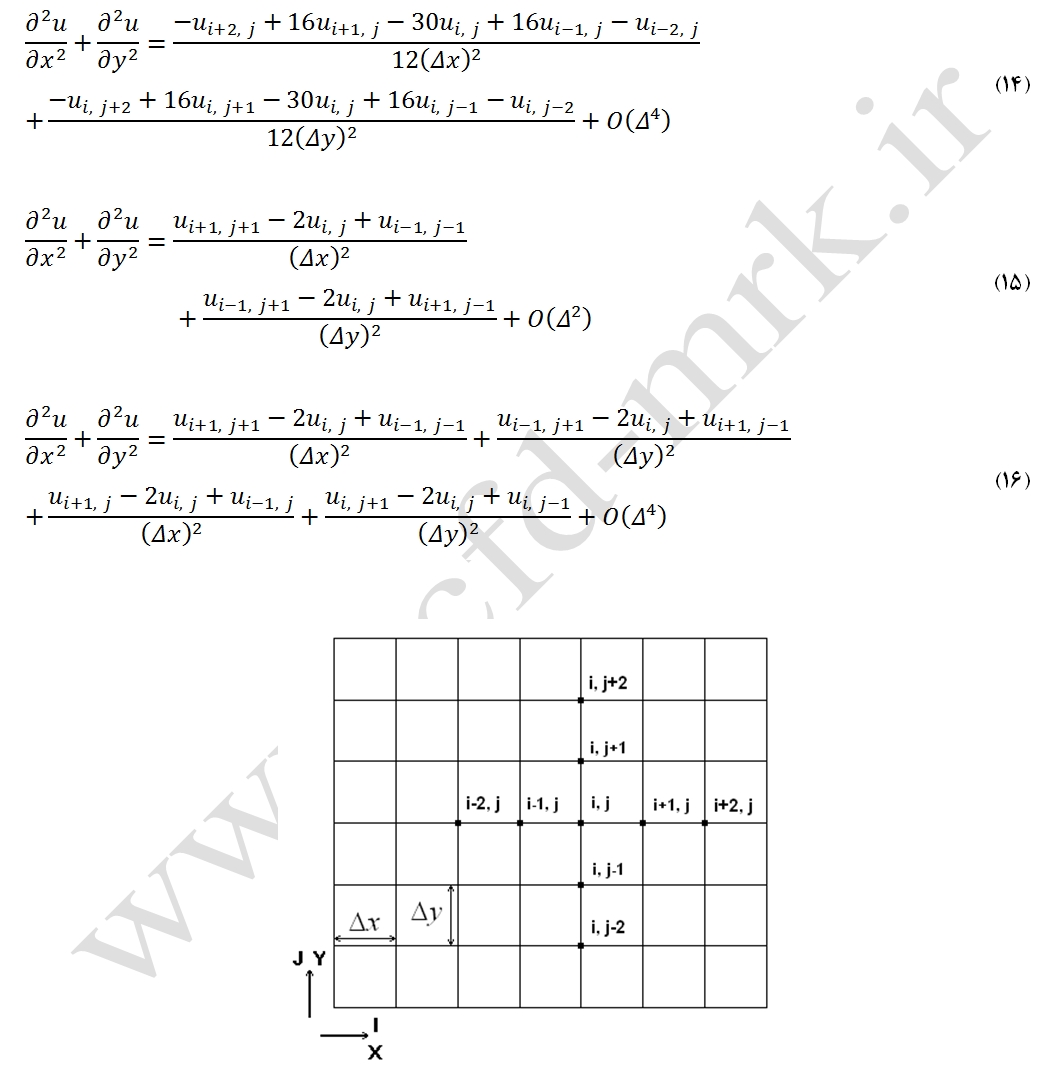
شکل-2: گره‌های درگیر شبکه در روش فرمول نه نقطه.

فرمول پنج نقطه به نقطه می‌تواند بصورت استنسیل بعلاوه‌ای (شکل3) با فرمولاسیون معادله (13) یا استنسیل ضربدری (شکل 4) و با فرمولاسیون (15) یا ترکیبی از این دو (شکل5) با فرمولاسیون (16) بیان شود. هر چه تعداد گره‌های درگیر در معادلات گسسته‌سازی شده بیشتر باشد، پایداری آن روش بیشتر است. بنابراین استنسیل ترکیبی پایدارتر از استنسیل‌های بعلاوه و ضربدری است. البته بسته به نوع مسئله، کارایی این نوع استنسیل‌ها تفاوت دارد. بعنوان مثال در انتقال حرارت هدایت در یک صفحه فلزی، بمنظور دخالت دادن مقادیر مرزها در گوشه‌ها بهتر است از استنسیل‌های ضربدری استفاده نمود.

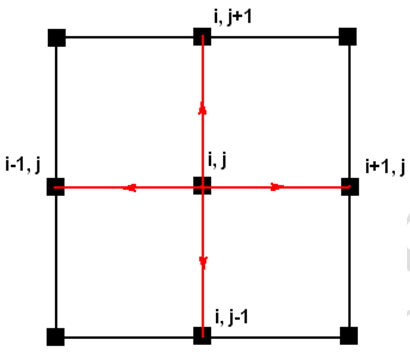
شکل-3: استنسیل بعلاوه‌ای.

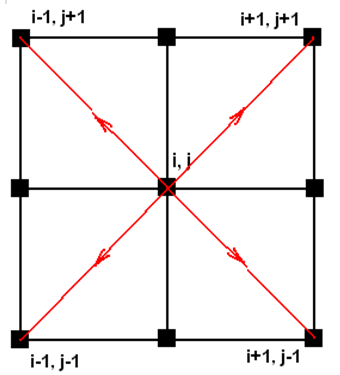
شکل-4: استنسیل ضربدری.

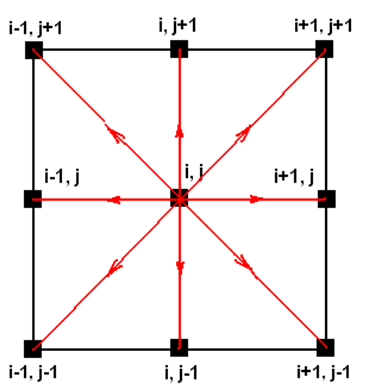
شکل-5: استنسیل ترکیبی.

بطور کلی روش‌های حل سیستم دستگاه معادلات جبری به دو دسته مستقیم و تکرار تقسیم می‌شود (اینجا). روش‌های حل مستقیم شامل روش‌های کرامر و حذفی گوس می‌باشد که خصوصیات آنها در اینجا توضیح داده شده است. این روش‌ها معمولاً دارای محدودیتهایی نظیر محدود بودن به سیستم دستگاه مختصات کارتزین، دامنه مکعب مستطیلی، شرائط مرزی، حافظه زیاد رایانه و همچنین مشکلات برنامه‌نویسی است. روش‌های حل تکرار خود نیز به دو دسته تکرار نقطه‌ به نقطه (Point by Point ) (تنها دارای یک مجهول) و روش‌های تکرار خط به خط(Line by Line ) (معمولاً دارای سه مجهول) تقسیم می‌شود. بطور کلی روش‌های حل تکرار محدودیتهای روش‌های حل مستقیم را ندارد. در ادامه انواع روش‌های حل تکرار برای حل سیستم معادلات دیفرانسیل جزئی بیضوی توضیح داده می‌شود. همچنین، کاربرد هر یک از روش‌های فوق در قالب مثال-1 بیان می‌شود.

 

مثال-1:

بعنوان اولین مثال، توزیع دما در حالت پایا در داخل یک صفحه چهار ضلعی دو بعدی مورد بررسی قرار گرفته است. ابعاد صفحه مذکور 1 متر در جهت X و 2 متر در جهت Y می‌باشد (شکل 6). شرائط مرزی دمایی نیز در همین شکل نشان داده شده است. از آنجائیکه مقادیر روی مرزها مشخص است، شرط مرزی از نوع شرط مرزی دریشله (Dirichlet) خواهد بود. معادله دیفرانسیل جزئی حاکم بر این مسئله (انتقال حرارت هدایت دو بعدی)، بصورت معادله (17) می‌باشد.

شرائط مرزی اعمالی روی سطح مذکور از قرار زیر است:

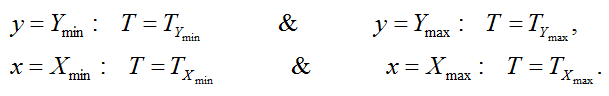
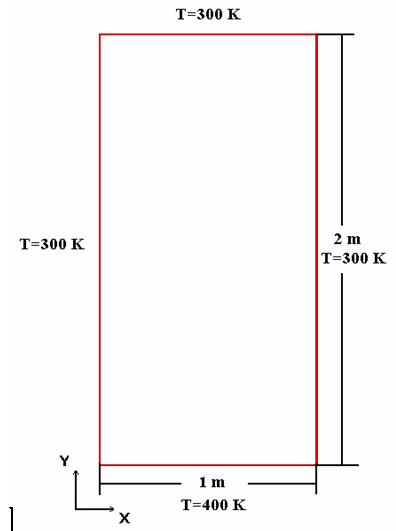
شکل-6: صفحه تخت چهارضلعی با توزیع ثابت دما در مرزها.

پس از بررسی استقلال جواب‌ها از شبکه (همانند شکل-9)، در تمامی روش‌های عددی، دامنه محاسباتی 20 المان در جهت x و 40 المان در جهت y دارد (شکل-7). 

روش‌های نقطه به نقطه در حل معادلات بیضوی به روش تفاضل محدود

در واقع روش‌های نقطه به نقطه معادل روش‌های صریح و روش‌های خط به خط معادل روش‌های ضمنی در مسائل همراه با ترم زمانی است. روش‌های نقطه به نقطه در حل عددی معادله لاپلاس شامل روش‌های تکرار نقطه‌ به نقطه ژاکوبی، تکرار نقطه‌ به نقطه گوس-سایدل و تکرار نقطه‌ به نقطه خلاصی می‌باشد. در ادامه هر یک از این رو‌ها توضیح داده شده است. 

 

روش تکرار نقطه‌ به نقطه ژاکوبی (Jacobi Point Iterative Method)

در این روش، متغیر وابسته در هر گره بر اساس مقادیر گره‌های همسایه (مقادیر در نظر گرفته شده از حدس اولیه و یا مقادیر محاسبه شده در تکرار قبل) محاسبه می‌شود. معادله (18) بیانگر روش تکرار نقطه‌ به نقطه ژاکوبی برای محاسبه مقدار u^k+1_i,j در تکرار k+1 می‌باشد. در این رابطه β=∆x/∆y و k مرحله تکرار قبلی است. محاسبات تا زمانی که جواب‌ها به همگرایی دلخواه برسد ادامه می‌یابد. همگرایی دلخواه زمانی تحقق پیدا می‌کند که باقیمانده پاسخها از مقدار معینی کمتر شود (Err). برای محاسبه Err از رابطه (19) استفاده می شود.

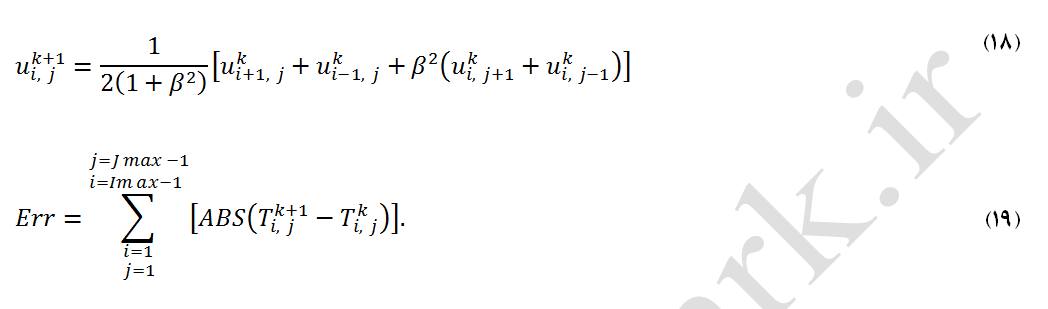
در رابطه فوق I_max و J_max تعداد المانها در جهت‌های x و y است. برای حل عددی مثال-1 با استفاده از این روش کافیست با جایگذاری T بجای u در معادله (18)، آن را حل کرد. جوابهای بدست آمده در شکل‌های (8) و (9) نشان داده شده است.

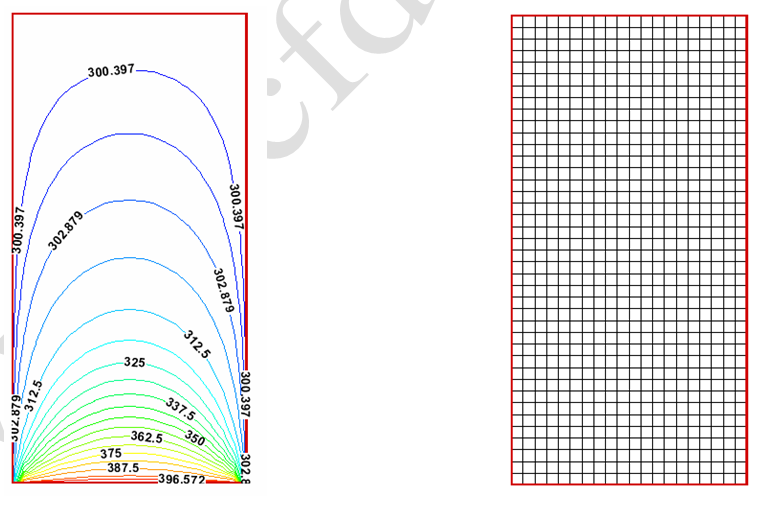
شکل-7: شبکه عدد تولید شده برای مثال-1.                                                 شکل-8: توزیع دما روی سطح با روش تکرار نقطه به نقطه ژاکوبی.

 

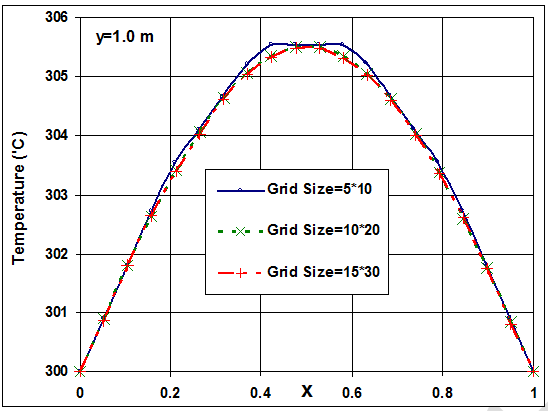
شکل-9: چگونگی تغییرات توزیع دما در مقطع میانی سطح (جهت y) نست به ابعاد شبکه.

در شکل (8) توزیع دما روی سطح نشان داده شده که بصورت نیم بیضی است. همانطور که قبلاً اشاره شد، در هر کار عددی، تعداد شبکه باید بگونه‌ای باشد تا جواب‌های بدست آمده مستقل از شبکه باشند. به همین خاطر، توزیع دما برای شبکه‌های مختلف در شکل (9) رسم شده است. همانطور که در این شکل مشخص است تفاوت چندانی در جواب‌های نهایی بین شبکه‌های 20*10 و 30*15 وجود ندارد. با این حال برای اطمینان از اینکه تمامی روش‌های عددی بکار رفته مستقل از شبکه باشند از شبکه 40*20 برای همه آنها استفاده شده است.

 

روش تکرار نقطه‌ به نقطه گوس-سایدل (Gauss-Seidel Point Iterative Method)

در روش مذکور هر متغیر وابسته به هر یک از گره‌های محاسباتی بلافاصله پس از محاسبه شدن در هر تکرار در محاسبات بعدی مورد استفاده قرار می‌گیرد. جزئیات بیشتر این روش در اینجا آمده است. با بکارگیری این روش سرعت همگرایی بطور قابل ملاحظه‌ای در حدود 100%  نسبت به روش تکرار نقطه به نقطه ژاکوبی (جدول 1) افزایش می‌یابد (شکل‌های 20 و 21).  فرم کلی گسسته‌سازی با این روش در قالب روش اجزاء محدود بصورت معادله (20) است. نتیجه بدست آمده در شکل (10) نشان داده شده است.

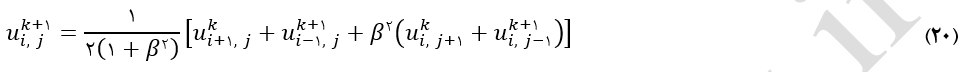
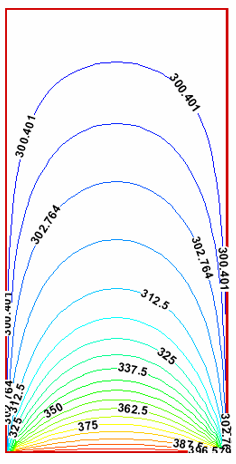
شکل-10: توزیع دما روی سطح با روش تکرار نقطه به نقطه گوس-سایدل.

 

روش تکرار نقطه‌ به نقطه خلاصی (Point Relaxation Iterative Method)

در روش‌های تکرار، فرآیند حل از یک حدس اولیه شروع شده و تا حل پایدار ادامه می‌یابد. چنانچه در طی فرآیند حل، روند و رفتار مقادیر محاسبه شده متغیرهای وابسته مد نظر باشد، جهت تغییرات می‌تواند برای برونیابی این متغیرها در تکرار بعدی مورد استفاده قرار گیرد. بنابراین نرخ همگرائی افزایش قابل توجهی نسبت به روش تکرار نقطه به نقطه ژاکوبی (برای مثال-1 بطور میانگین 15 برابر) و روش تکرار نقطه به نقطه گوس-سایدل (برای مثال-1 بطور میانگین 7.5 برابر) افزایش می‌یابد. این مهم در جدول (1) و شکل‌های (20) و (21) نشان داده شده است. متد حاضر با عنوان روش تکرار نقطه به نقطه یا خط به خط خلاصی شناخته شده است. علاوه براین برای مسائلی که همگرائی آنها به سادگی امکان‌پذیر نباشد، می‌توان با انتخاب مناسب ضریب خلاصی، همگرائی را بهبود بخشید.

برای رسیدن به فرمولاسیون روش نقطه‌ به نقطه خلاصی ابتدا به روش تکرار نقطه به نقطه گوس سایدل (معادله 20) که مبنای این روش می‌باشد، توجه شود. با افزودن ترم  u^k_i,j – u^k_i,jبه سمت راست معادله مذکور و جمع کردن آن با ترمهای دیگر معادله (21) حاصل می‌شود. بعنوان فرآیند حل، u^k_i,j باید u^k+1_i,j را تقریب بزند. به منظور شتاب دادن به روند همگرائی حل، ترم داخل کروشه در ضریب خلاصی، ω، ضرب می‌شود (معادله22). با مرتب سازی این معادله، فرم نهایی گسسته‌سازی معادله لاپلاس با روش تکرار نقطه‌ به نقطه خلاصی بصورت معادله (23) نوشته می‌شود. برای ω=1 این روش معادل روش تکرار نقطه‌ به نقطه گوس-سایدل می‌باشد. همچنین، برای مقادیر ω<1 این روش با عنوان روش زیر خلاصی (Under Relaxation) و برای ω>1  با عنوان روش فوق خلاصی (Over Relaxation) نامیده می‌شود.

مهمترین سئوالی که در این روش مطرح می‌باشد اینست که چگونه می‌توان مقدار بهینه‌ای برای ω پیدا کرد؟ در پاسخ می‌توان گفت که در واقع هیچ راهکار مشخصی برای یافتن مقدار بهینه ω وجود ندارد. اما برای کاربردهای محدودی، چندین رابطه برای یافتن مقدار بهینه ω پیشنهاد شده است. یکی از این روابط برای حل معادلات بیضوی در دامنه مربع-مستطیل با شرط مرزی دریشله در معادله (24) نشان داده شده است.

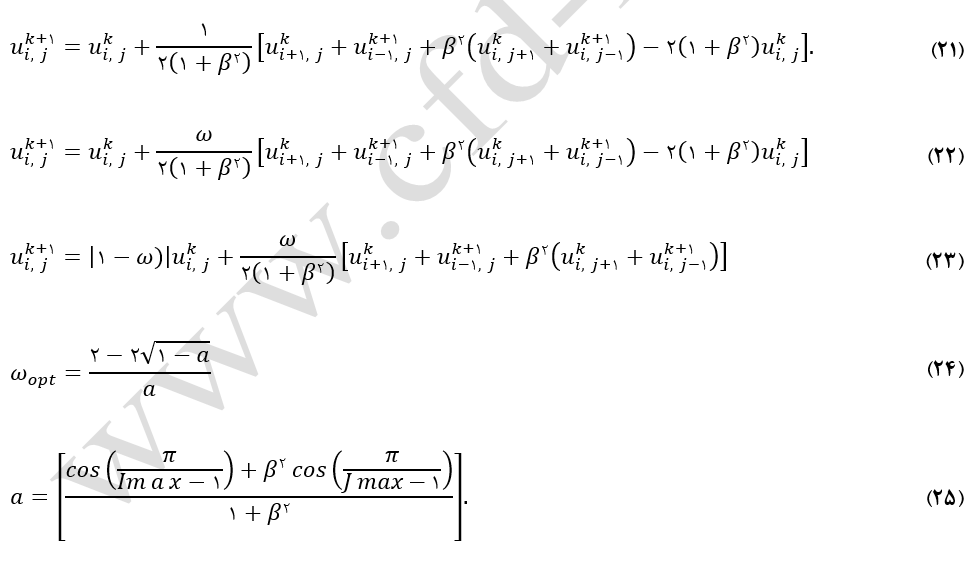
با استفاده از معادله (24) مقدار بهینه ω برای مثال-1 برابر 1.995 تقریب زده می‌شود، در صورتیکه مقدار بهینه واقعی تقریباً برابر 1.85 می‌باشد. در شکل (11) نمودار تعداد تکرار مورد نیاز برای همگرایی نسبت به مقادیر مختلف ضریب خلاصی نشان داده شده است. همچنین توزیع دما برای مقدار بهینه ضریب خلاصی (1.85) در شکل (12) نشان داده شده است.

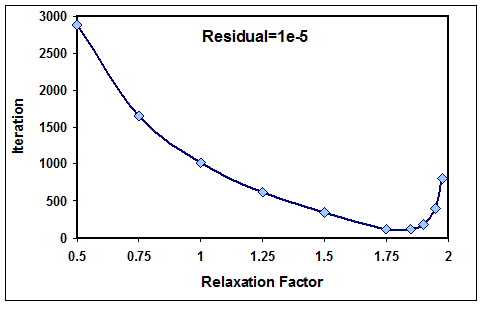
شکل-11: ضریب خلاصی و تعداد تکرار متناظر برای همگرائی با روش نقطه‌ به نقطه خلاصی.

 

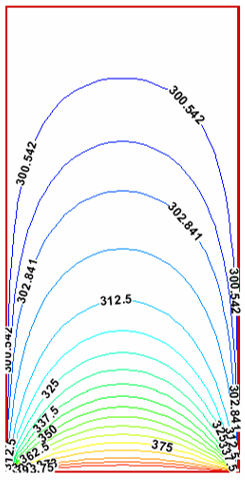
شکل-12: توزیع دما روی سطح با روش تکرار نقطه به نقطه خلاصی.

 

روش‌های خط به خط در حل معادلات بیضوی به روش تفاضل محدود

همانطور که اشاره شد روش‌های خط به خط معادل روش‌های ضمنی در مسائل وابسته به زمان است. مهمترین روش‌های خط به خط در حل عددی معادل لاپلاس شامل روش‌های خط به خط گوس-سایدل و روش‌های خط به خط خلاصی است که در ادامه توضیح داده می شود.

 

روش تکرار خط به خط گوس-سایدل (Gauss-Seidel Line Iterative Method)

در این روش در هر تکرار گره‌های محاسباتی در هر یک از ردیف‌های سطری یا ستونی شبکه همزمان در محاسبات لحاظ گشته و در نتیجه لازمست که برای هر ردیف دستگاه معادلات حل شود. بعبارت دیگر در هر معادله سه متغیر وابسته مجهول بعنوان مثال در گره‌های (i-1, j)، (i, j) و (i+1, j) وجود دارد (اینجا) که فرمولاسیون آن برای 2<i و i<I_max-1  طبق معادله (26) می‌باشد. معادله مذکور در هر j ثابت، از تمامی گره‌های موجود در ردیف i (که بصورت گره‌های مربع شکل در شکل (13) نشان داده شده است) را برای انجام محاسبات استفاده می‌کند. حاصل این امر تولید یک دستگاه معادلات با ماتریس ضرائب سه قطری است.

در شکل (13) گره‌های لوزی شکل بیانگر شرط مرزی، گره‌های ضربدر معرف مقادیر معلوم در تکرار k+1، گره‌های مربع نشان دهنده مجهولات در تکرار k+1 که باید محاسبه شوند و در نهایت گره‌های دایره شکل مقادیر معلوم در تکرار k می‌باشد. همچنین، باید توجه داشت که بمنظور اعمال شرائط مرزی سمت راست معادله (26) برای ردیفهای i=1، i=2 و i=I_max-1 بصورت روابط (27) نوشته می‌شود.

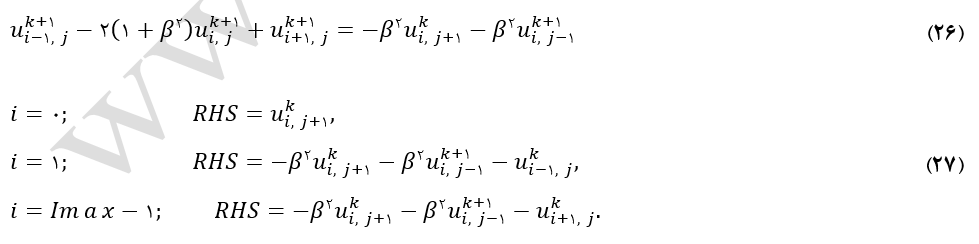
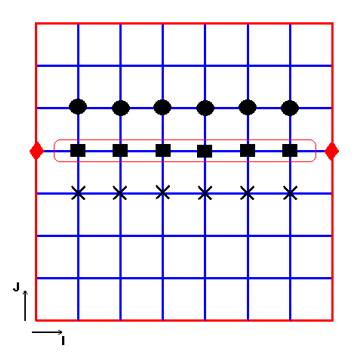
شکل 13: چگونگی قراگیری مقادیر مجهول و معلوم در روش تکرار خطی گوس سایدل.

استفاده از روش خط به خط گوس-سایدل موجب افزایش هشتاد تا نود درصدی سرعت همگرائی نسبت به روش نقطه به نقطه گوس-سایدل می‌شود. اما در هر تکرار مقدار زمان مورد نیاز برای انجام محاسبات در این روش بمراتب بیشتر از روش نقطه به نقطه گوس-سایدل است. در شکل (14) توزیع دمای بدست آمده با روش خط به خط گوس-سایدل نشان داده شده است. بطور کلی در مسائلی که تغییرات متغیرهای وابسته در یک جهت خاص قابل توجه باشد، بهتر است که از روش تکرار خط به خط گوس-سایدل در آن جهت استفاده کرد.

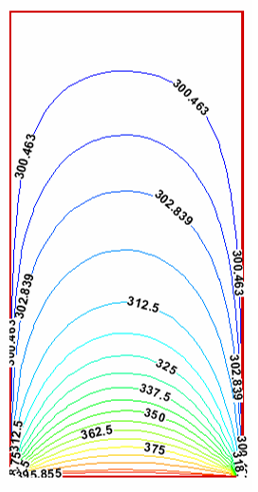
شکل-14: توزیع دما روی سطح با روش تکرار خط به خط گوس-سایدل.

 

روش تکرار خط به خط خلاصی (Line Relaxation Iterative Method)

همانند روش تکرار نقطه به نقطه خلاصی، روش تکرار خط به خط خلاصی نیز از یک ضریب خلاصی در معادله جبری حاکم استفاده می‌کند. با انجام راهکار مشابه در قسمت (روش نقطه به نقطه خلاصی) فرم نهایی روش تکرار خط به خط خلاصی برای 2<i و i<I_max-1 بصورت معادله (28) می‌باشد. به منظور اعمال شرائط مرزی سمت راست معادله (28) برای ردیف‌هایi=1، i=2 و i=I_max-1 بصورت روابط نشان داده شده در دسته معادلات (29) نوشته می‌شود.

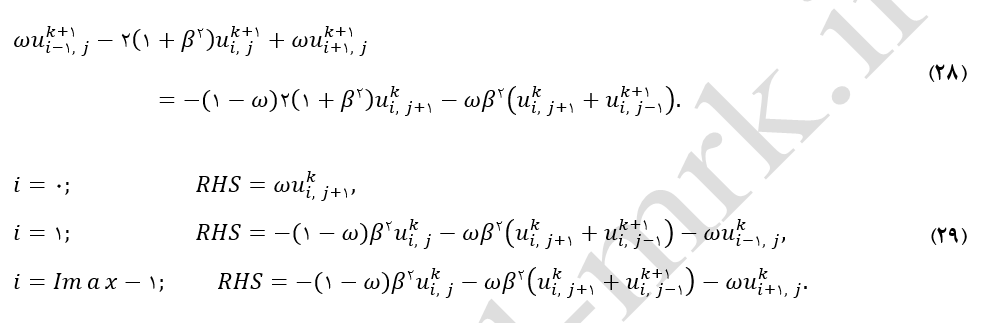
هیچگونه روش معینی برای یافتن مقدار بهینه ω وجود ندارد. در واقع از روش سعی و خطا برای تعیین مقدار مناسب ω استفاده می‌شود. در شکل (15) تغییرات تعداد تکرار نسبت به ضریب خلاصی و در شکل (16) توزیع دمای محاسبه شده با استفاده از این روش نشان داده شده است.

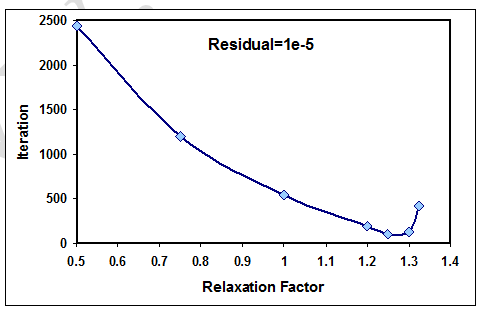
شکل-15: ضریب خلاصی و تعداد تکرار متناظر برای همگرائی با روش خط به خط خلاصی.

 

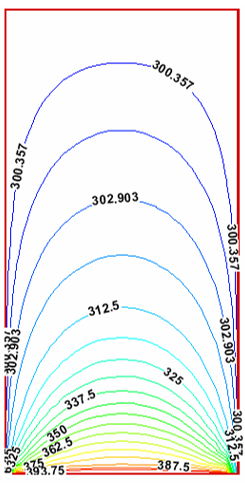
شکل-16: توزیع دما روی سطح با روش تکرار خط به خط خلاصی.

 

روش‌(Alternative Direction Implicit (ADI))

روش ADI در واقع یک روش خط به خط است که معادلات در هر تکرار یک بار در جهت سطری و یک بار در جهت ستونی (شکل 17) و یا برعکس حل می‌شود. فرم معادلات بکار رفته در این روش بصورت معادلات (30) و (31) است. ابتدا در معادله (30) متغیرها بطور ضمنی در جهت i حل شده و سپس بعنوان مقادیر تصحیح شده بطور ضمنی و در جهت j حل می‌شود. فرآیند حل و درگیر شدن گره‌ها در محاسبات در شکل (17) نشان داده شده است. روند حل را می‌توان با دخالت دادن ضریب خلاصی، ω، در معادلات (30) و (31) سرعت بخشید. فرم تصحیح شده این معادلات در معادلات (32) و (33) نشان داده شده است. همانند سایر روش‌ها، از آنجا که یافتن مقدار بهینه برای ω بسیار مشکل می‌باشد، تنها راه حل عملی، بررسی تجربی همراه با سعی و خطای روند حل با مقادیر مختلف ω است.

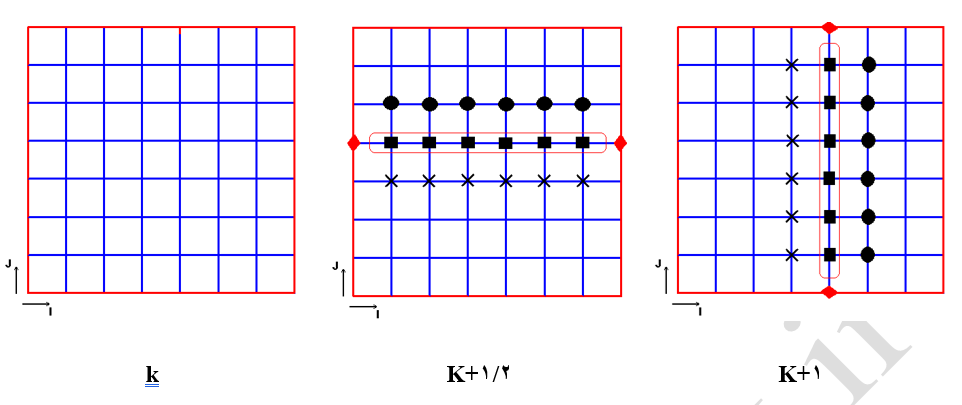
شکل-17: چگونگی چیدمان گره‌های استفاده شده در محاسبات برای هر تکرار.

فرمولاسیون فوق تنها فرم ساده‌ای از حل معادلات دیفرانسیل جزئی به روش ADI است. بسته به نوع معادلات و کاربردهای آن فرمولاسیون این روش متفاوت خواهد بود. سرعت همگرائی در این روش نیز بطور قابل توجهی نسبت به سایر روش‌های خط به خط و همچنین روش‌های خلاصی بیشتر است. در شکل (18) تغییرات سرعت همگرائی نسبت به مقادیر مختلف ضریب خلاصی نشان داده شده است. شکل (19) نیز نمایشگر توزیع دمای بدست آمده با استفاده از این روش می‌باشد.

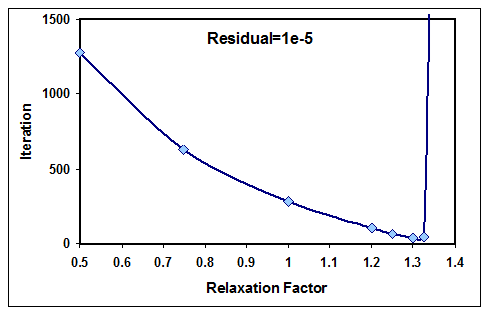
شکل-18: ضریب خلاصی و تعداد تکرار متناظر برای همگرائی با روش ADI.

 

شکل-19: توزیع دما روی سطح با روش ADI.

مقایسه بین روش‌های تکرار

از آنجا که در حل عددی مسائل با روش‌های تکرار بحث تعداد تکرار و زمان همگرا شدن محاسبات مطرح است، لذا در این قسمت سعی شده روش‌های اشاره شده در قسمت‌های قبل، از لحاظ تعداد تکرار مورد نیاز برای همگرائی مورد مقایسه قرار گیرند. باید توجه داشت که در بسیاری از مسائل، بعلت پیچیدگی، معادلات حاکم (بعنوان مثال غیر خطی بودن معادلات)، حجم شبکه، حافظه مورد نیاز و خیلی موارد دیگر قبل از اینکه تعداد تکرار مطرح باشد، همگرائی آنها مهم است. به همین خاطر تأکید می‌شود که این مقایسه تنها در مورد نرخ همگرائی یک مسئله خاص بوده و بهترین این روش‌ها از لحاظ نرخ همگرائی الزاماً روش بهینه برای تمامی مسائل این دسته معادلات نخواهد بود.

همه روش‌های فوق که در مثال-1 استفاده شده با یکدیگر مقایسه شده است. مقدار باقیمانده برای همه این روش‌ها یکسان می‌باشد. نتایج حاصل از مقایسه این روش‌ها در جدول (1)، شکل (20) و نمودار شکل (21) نشان داده شده است.

جدول-1: تعداد تکرار مورد نیاز برای همگرائی در روش‌های مختلف.

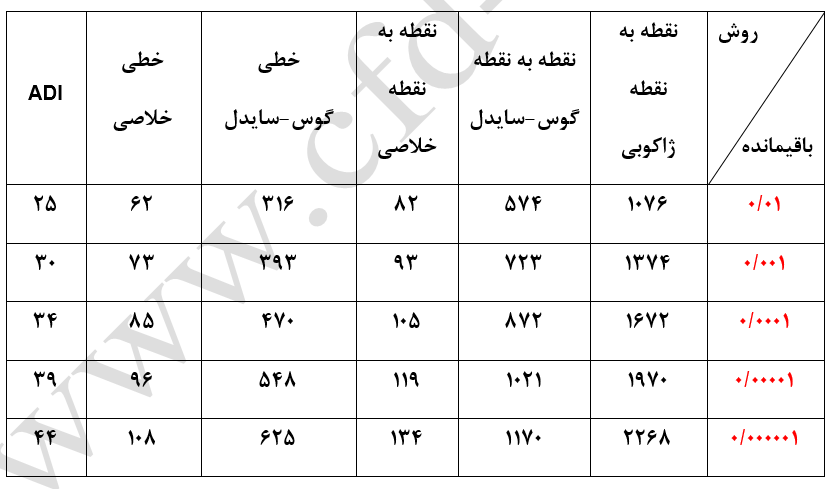
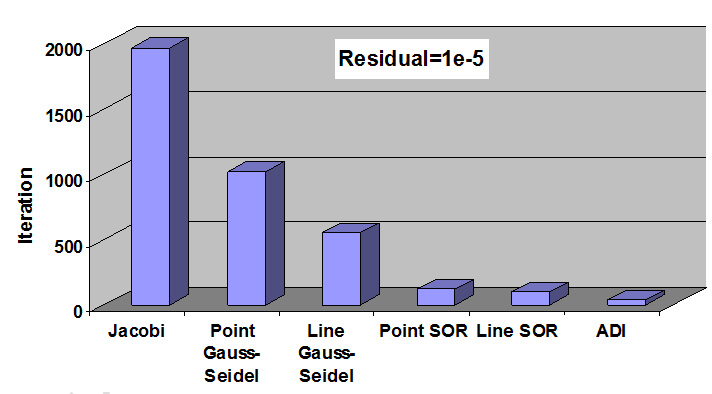
شکل-20: تعداد تکرار مورد نیاز برای همگرائی در روش‌های مختلف.

 

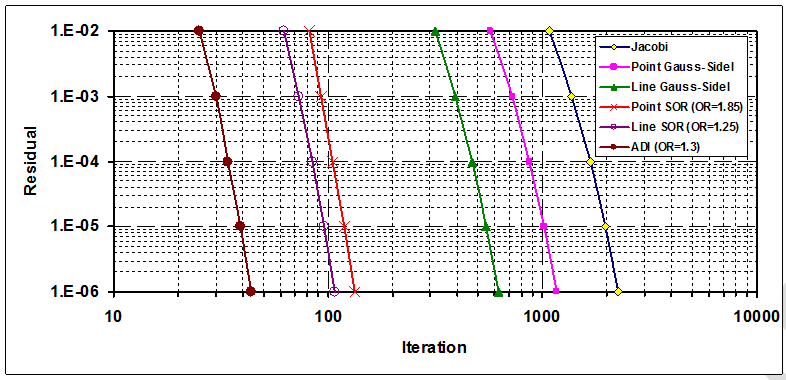
شکل-21: تعداد تکرار مورد نیاز برای همگرائی روش‌های مختلف بر اساس باقیمانده 0.00001.

نتایج نشان می‌دهد که روش‌های تکرار نقطه به نقطه ژاکوبی و ADI به ترتیب دارای کمترین و بیشترین سرعت همگرائی هستند. با نگاهی گذرا به فرمولاسیون این روش‌ها می‌توان دریافت که فرمولاسیون و الگوریتم برنامه‌نویسی برای نقطه به نقطه ژاکوبی ساده‌ترین و برای ADI مشکلترین درتمام روش‌های یاد شده می‌باشد. نکته دیگر اینکه سرعت همگرائی در روش تکرار نقطه به نقطه خلاصی بطور قابل توجهی از روش تکرار خط به خط گوس-سایدل بیشتر است. این مسئله خاطر نشان می‌کند که ضریب خلاصی نقش انکار ناپذیری در روند همگرائی روش‌های تکرار بازی می‌کند، تا حدی که انتخاب بهینه ضریب خلاصی در روش‌های نقطه به نقطه موجب افزایش سرعت همگرائی این روش‌ها نسبت به روش‌های صرفاً خط به خط و بدون ضریب خلاصی (بعنوان مثال روش تکرار نقطه به نقطه خلاصی نسبت به روش تکرار خط به خط گوس-سایدل) می‌شود.

به طور کلی، با نگاهی نافذتر به نتایج نشان داده شده می‌توان به این نتیجه رسید که هرچه تعداد گره‌های محاسباتی، مقادیر اصلاح شده (در هر تکرار) و برونیابی مناسب متغیرهای وابسته در هر روش بیشتر باشد سرعت همگرائی آن روش بیشتر می‌شود.