تولید شبکه روی خط

تولید شبکه روی خط (توزیع نقاط روی خط یا همان شبکه بندی لبه)

Edge Meshing

اساس شبکه بندی در مسائل CFD بر تولید شبکه روی خط یا خطوط مرزی وابسته است. در واقع شبکه بندی خطوط مرزی با تراکم و چیدمانی مناسب شرط لازم برای تولید شبکه با کیفیت می‌باشد. به عبارت دیگر برای شبکه‌بندی سطوح و احجام تعداد نقاط محاسباتی (نودها) و همچنین نحوه چیدمانی آنها روی خطوط (لبه‌ها) بسیار مهم هستند. بنابراین می‌توان دریافت که برای مش بندی خطوط، باید دو پارامتر مهم تعداد (تراکم) و توزیع (چیدمانی) گره‌های محاسباتی را مشخص نمود.

 

تعداد المان‌ها در تولید شبکه روی خط

اولین گام در شبکه بندی خطوط تعیین تعداد المان‌ها می‌باشد. نکته مهم اما کافی بودن تعداد المان‌هاست. به ندرت پیش می‌آید که تراکم شبکه بندی سطح و حجم از تراکم شبکه خطی بیشتر باشد. به عبارت دیگر بسیار بعید است که حداقل اندازه اضلاع المانهای سطح و حجم از حداقل اندازه المانهای خط کمتر شود. در نتیجه اندازه المان‌های لبه اهمیت بسیاری دارد. روش‌های متعددی وجود دارد که با استفاده از آن‌ها بتوان به طور مستقیم یا غیر مستقیم تعداد المان‌های خط را مشخص نمود.

همانطور که اشاره شد، تعداد المان‌ها را می‌توان به صراحت مشخص نمود. مثلا در برنامه نویسی (کد نویسی) برای شبکه بندی، تعریف و تعیین یک متغیر برای تعداد المان‌ها امری بدیهی است. در شبکه بندی با استفاده از نرم افزارها نیز هر یک از نرم افزارها از اصطلاح و متغیر منحصر به خود برای تعیین تعداد المان‌ها برخوردار هستند. به عنوان مثال در نرم افزار Gambit از اصطلاح (Interval Count)، نرم افزار Ansys Meshing از اصطلاح (Number of Divisions) و نرم افزار ICEM-CFD از اصطلاح (Nodes) -که البته در این نرم افزار، تعداد المان‌ها از تعداد Nodes یکی کمتر است- برای تعریف تعداد المان‌ها در هر خط (لبه) استفاده می‌شود.

می‌توان به طور غیر مستقیم نیز تعداد المان‌ها در هر خط یا لبه را مشخص نمود. اگر اندازه المان‌های هر خط را ثابت فرض کنیم با تعیین اندازه المان، تعداد المان‌ها مشخص می‌شود. به عبارت دیگر، با تقسیم طول خط بر اندازه المان تعداد المان به دست می‌آید. البته اگر حاصل این تقسیم یک عدد طبیعی نباشد می‌توان با گرد کردن محاسبات تعداد المان‌ها را مشخص کرده و سپس اندازه خط را بر این تعداد تقسیم کرده تا اندازه هر المان به دست آید. به عنوان مثال با استفاده از پارامتر (Interval Size) در نرم افزار Gambit و Element Size در نرم افزار Ansys Mesh اندازه المان‌ برای شبکه بندی لبه‌ها مشخص می‌شود.

روش‌های دیگری نیز برای تعیین تعداد المان‌ها وجود دارد. در نرم افزار Gambit از پارامتر Shortest Edge%  برای تعیین تعداد المان‌ها بر اساس درصدی از اندازه کوچکترین خط (لبه) موجود در مدل هندسی استفاده می‌شود. پارامترهای  کره تأثیر  (Sphere of Influence) و فاکتوری از اندازه کلی (Factor of Global Size) از پارامترهای دیگری هستند که برای تعیین تعداد المان‌ها در نرم افزار Ansys Meshing به کار می‌روند. در بحث برنامه نویسی کامپیوتری نیز هیچ گونه محدودیتی برای تعریف پارامترهای مناسب برای تعیین تعداد المان روی خطوط وجود ندارد.

 

توزیع المان‌ها در تولید شبکه روی خط

با معلوم شدن تعداد المان‌ها نوبت به توزیع آن روی خط می‌شود. توزیع المان‌ها ارتباط مستقیم با توزیع نودهای محاسباتی روی خط دارد. هر المان فاصله بین دو نود (نقطه) می‌باشد که در نتیجه تعداد المان‌های هر لبه (خط) از تعداد نودهای آن لبه یکی کمتر است. برای توزیع نقاط از توابع متنوعی که معمولا از نوع توابع جبری یا مثلثاتی هستند استفاده می‌شود. توزیع المان‌ها روی یک خط می‌تواند یک طرفه (از یک سمت) یا دو طرفه (از هر دو سمت) باشد. در اینجا مهمترین توابع توزیع نقاط روی خطوط یا همان نودهای محاسباتی روی لبه‌ها معرفی شده‌اند.

پیش از پرداختن به توابع توزیع نقاط ابتدا پارامترهای توزیع شبکه روی لبه معرفی شده است. در شکل (1) پارامترهای اصلی برای شبکه بندی خطوط نشان داده شده است. همانطور که در شکل پیداست هر خط(لبه) دارای جهت از نقطه شروع (Start) به نقطه پایان (End) می‌باشد. l₁، l₂،… و l_n به ترتیب اندازه المان‌‌های 1، 2 و n (آخر) هستند. R هم نرخ رشد (مقدار ثابت اندازه هر المان به المان قبلی خود) است که در تمام طول خط (لبه) ثابت باقی می‌ماند. سه پارامتر l₁، l_n (که در برخی نرم افزارها به عنوان l₂ نیز تعریف می‌شود) و R در تمامی توابع توزیع نقاط نقشی انکار ناپذیر دارند.

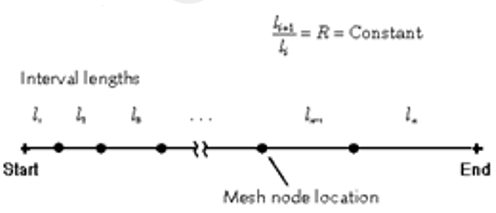
شکل-1: پارامترهای توزیع نقاط (نودهای محاسباتی) روی یک خط (لبه).

 

توزیع یک طرفه المان‌ها در تولید شبکه روی خط

در توزیع یک طرفه، تراکم المان‌ها از ابتدای خط (لبه) به انتهای آن و بر عکس تغییر می‌کنند. با توجه به شکل بالا اولین المان در ابتدای لبه (نقطه Start یا نقطه 1) و آخرین المان در انتهای لبه (تقطه End یا نقطه 2 یا n) قرار دارد. جهت لبه‌ها نیز از نقطه Start به نقطه End تعریف می‌شود.

معمولا در ادبیات تولید شبکه اولین المان را با اصطلاح First (همانند نرم افزار Gambit) یا با شماره 1 (همانند نرم افزار ICEM-CFD) می‌شناسند. همینطور آخرین المان را با حرف n، اصطلاح  Last (همانند نرم افزار Gambit) یا با شماره 2(همانند نرم افزار ICEM-CFD) نام می‌برند. همینطور طول هر المان با عناوینی همچون length (مثل نرم افزار Gambit) یا Spacing (در نرم افزار ICEM-CFD) تعریف می‌شود. به هر حال در برنامه نویسی کامپیوتری برای تولید شبکه شما مختارید هر نامی را که دلتان می‌خواهد انتخاب کنید!

در شکبه بندی یک طرف لبه‌های تراکم المان‌ها ممکن است در ابتدا یا انتهای لبه‌ها بیشتر باشد (شکل-2) یا اینکه حتی یکسان باشد و المان‌ها هم اندازه باشند. توابع بسیاری برای توزیع المان‌ها یا همان تراکم شبکه روی لبه‌ها پیشنهاد شده اند. برخی از آن‌ها از ابتدای خط (اولین المان) و برخی دیگر بر اساس انتهای خط (آخرین المان) هستند. در ادامه مهمترین و پرکاربردترین این توابع معرفی شده است.

شکل-2: توزیع یک طرفه نقاط روی خط از ابتدا یا انتهای خط

(طول خط بدون بعد در نظر گرفته شده است).

 

نسبت متوالی (Successive Ratio)

با دانستن مقادیر نرخ رشد، R و تعداد المان خط (لبه)، تراکم المان‌ها روی هر خط مشخص شده و به اصطلاح خط یا همان لبه شبکه بندی می‌شود (شکل-2). این تابع بسته شبکه بندی از ابتدا یا انتهای همانند معادلات (1) یا (2) قابل تعریف است و در نرم‌افزار Gambit برای شبکه بندی لبه‌ها در دسترس است.

 

طول اولین المان (First Length)

در این روش از یک رابطه جبری ساده برای توزیع نقاط روی خط استفاده می‌شود. برای اینکار کافیست طول اولین المان لبه، l₁، را مشخص کنیم. تابع مذکور در معادله (1) مندرج در جدول (1) نشان داده شده است.

 

طول آخرین المان (Last Length)

در این روش همانند روش قبل از یک رابطه جبری ساده برای توزیع نقاط روی خط استفاده می‌کند. برای اینکار کافیست بر خلاف روش قبل، طول آخرین المان لبه، l_n، را مشخص کنیم. تابع مذکور در معادله (2) نشان داده شده است.

 

نسبت طول اولین به آخرین المان (First Last Ratio)

یک تابع جبری براساس نسبت اولین المان به آخرین المان در یک مسیر، خط و یا لبه توسعه یافته است که برای توزیع نقاط از آن استفاده می‌شود. این تابع در معادله (3) نشان داده شده است.

 

نسبت طول آخرین به اولین المان (Last First Ratio)

برخلاف روش قبلی در این روش از یک تابع جبری براساس نسبت اولین المان به آخرین المان برای توزیع نقاط در یک مسیر، خط و یا لبه استفاده می‌شود. این تابع در معادله (4) نشان داده شده است.

 

تابع نمایی ابتدا (Exponential1)

در این متد فاصله هر گره محاسباتی i تا ابتدای هر لبه، x_i، با استفاده از تابعی با متغیرهای طول اولین المان، l₁، و نرخ رشد ابتدا، R₁، تعیین می‌شود (معادله 5).

 

تابع نمایی انتها (Exponential2)

رابطه نمایی انتها همان تابع نمایی ابتدا می‌باشد با این تفاوت که متغیرهای آن طول آخرین المان، l₂، و نرخ رشد انتها، R₂، تعیین می‌شود (معادله 6).

 

تابع هندسی ابتدا (Geometric1)

در این روش کافیست تنها اندازه اولین المان، l₁، را مشخص کنید. در ادامه فاصله هر یک از نودهای محاسباتی تا ابتدال لبه، x_i، با استفاده از معادله (7) به دست می‌آیند.

قابل توجه است در نرم افزار ICEM-CFD، مقدار نرخ رشد، R، بین 0.25 تا 4 محدود شده است.

 

تابع هندسی انتها (Geometric2)

این تابع همانند تابع هندسی ابتدا است با این تفاوت که باید اندازه آخرین المان، l₂ ، را در آن مشخص کنید (معادله 8).

 

تابع نیم کسینوسی ابتدا (HalfCosinus1)

در استفاده از یک تابع کسینوسی برای توزیع المان روی لبه‌ها شما هیچ کنترلی روی آن نخواهید داشت. چرا که بخاطر ماهیت این تابع اندازه اولین المان، l₁، و نرخ رشد، R، بصورت خودکار محاسبه می‌شوند. در این روش نرخ رشد متغیر است. تابع نیم کسینوسی ابتدا در معادله (9) نشان داده شده است. ذکر این نکته ضروریست که در اینجا xi  فاصله بدون بعد گره محاسباتی از ابتدای لبه می‌باشد.

 

تابع کسینوسی انتها (HalfCosinus2)

همانند روش بالا نیازی نیست که مقدار متغیری را تعیین کنید. این تابع در معادله (10) نشان داده شده است. ذکر این نکته ضروریست که در اینجا xi  فاصله بدون بعد گره محاسباتی از ابتدای لبه می‌باشد.

 

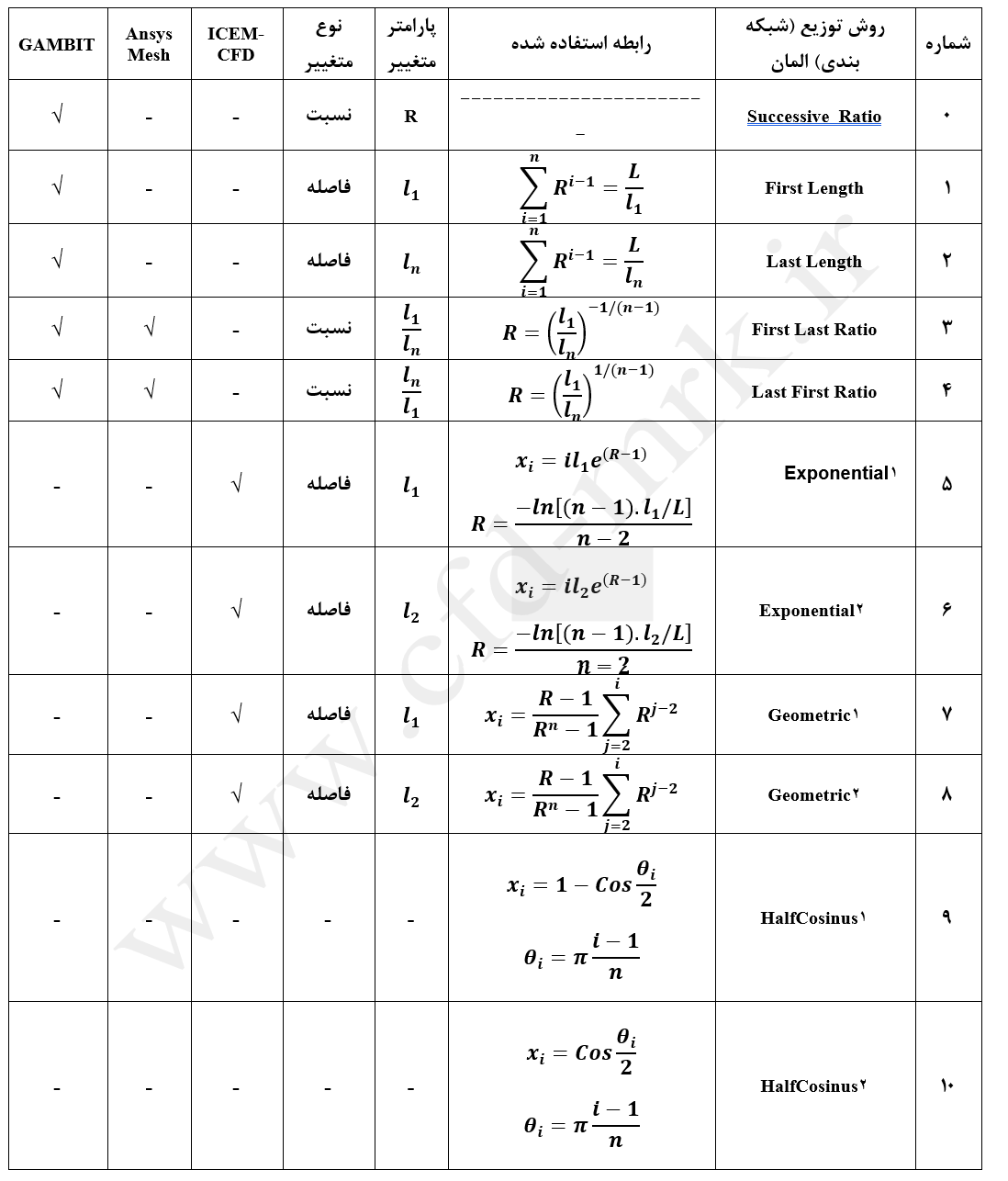
جدول-1: توابع مورد استفاده در توزیع یک طرفه المان‌ها روی لبه.

 

توزیع دو طرفه المان‌ها در تولید شبکه روی خط

در توزیع دو طرفه المان‌ها برای تولید شبکه روی خط دو راهکار وجود دارد. راهکار اول استفاده از توابع توزیع یک طرفه هماره با تقسیم لبه به دو نیم لبه و تولید شبکه برای هر یک از این دو نیم لبه می‌باشد. اما راهکار دوم به کارگیری معادلات ذاتا دو سویه مثل توابع کسینوسی، تانژانت هایپربولیک، سینوس هایپربولیک و غیره ارتباط دارد. برای راهکار اول تنها به چگونگی تقسیم لبه به دو نیم لبه بسنده شد چرا که توابع توزیع یک طرفه در بخش قبل توضیح داده شده است. در ادامه توابع توزیع دو طرفه نیز معرفی خواهد شد.

 

توزیع دو طرفه با تقسیم لبه به دو نیم لبه

برای شبکه‌بندی لبه با توابع توزیع یک طرفه باید مشخص شود که تقسیم بندی از یک طرف لبه انجام می‌شود یا از دو طرف آن. تفاوت مش بندی دو طرفه لبه اینست که بر خلاف حالت قبل از توزیع المان‌ها از دو طرف لبه انجام می‌شود. باید توجه داشت که نمی‌توان برای هر طرف نیم لبه‌ها از روشهای متفاوت شبکه‌بندی استفاده کرد. یعنی اینکه روش شبکه بندی برای هر دو طرف لبه باید یکی باشد.

در شبکه‌بندی دو طرفه یک لبه، یک گره یا یک المان، در مرز بین دو نیم لبه قرار می‌گیرد. این موضوع به زوج یا فرد بودن تعداد المان‌های تعریف شده، n، بستگی دارد (شکل-3). اگر تعداد المان‌ها زوج باشد یا به عبارت دیگر تعداد گره‌های روی لبه (شامل نقاط شروع و پایان) فرد باشد گره میانی شبکه بعنوان مرز دو نیم لبه و اگر تعداد گره‌‌های درون لبه زوج باشد آن وقت المان بین دو گره میانی شبکه بعنوان مرز میانی دو نیم لبه در نظر گرفته می‌شود. در ادامه هر دو نیم لبه با استفاده از یک تابع منتخب توزیع یک طرفه شبکه بندی می‌شوند.

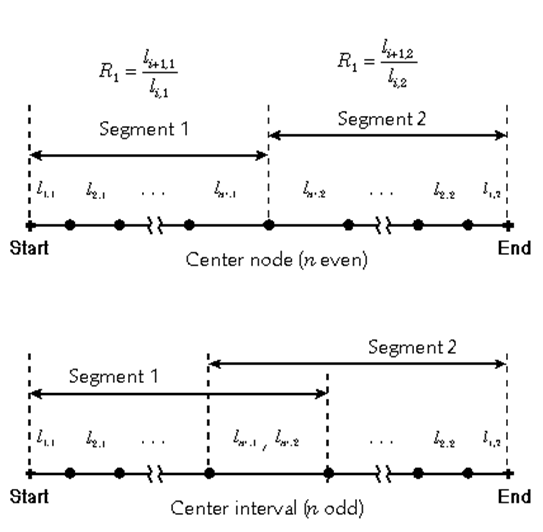
شکل-3: تقسیم لبه به دو نیم لبه و تعیین نود یا المان مرزی بین آن‌ها.

 

توابع توزیع دوطرفه

مهمترین توابع توزیع نقاط از دو طرف خط از توابع جبری و مثلثاتی تشکلیل می‌شود. هر چند توابع دیفرانسیلی مثل پوآسون نیز در توزیع دو طرفه المان‌ها روی لبه قابل استفاده است. در ادامه پر کاربردترین این نوع توابع توضیح داده شده است.

 

تابع کسینوسی کامل

این تابع هم همانند توابع یک طرفه کسینوسی به متغیری نیاز ندارد. فرم بدون بعد تابع مذکور در معادله (11) مندرج در جدول (2) نشان داده شده است. ذکر این نکته ضروریست که در اینجا xi  فاصله بدون بعد گره محاسباتی از ابتدای لبه می‌باشد.

 

تانژانت هایپربولیک

در روش تانژانت هایپر بولیک تنها لازم است طول‌های اولین المان، l₁، و آخرین المان، l₂ یا همان l_n، مشخص شوند. پس از آن توزیع نقاط با استفاده از معادلات (12) به دست می‌آید.

 

سینوس هایپربولیک

کلیات توزیع نقاط به روش سینوس هایپربولیک همانند روش تانژانت هایپربولیک است که تنها در جایگزینی سینوس هایپربولیک به جای تانژانت هایپربولیک تفاوت دارند. در این روش تابع توزیع نقاط روی دامنه محاسباتی به صورت دسته معادلات (13) تعریف می‌شود.

 

توابع زنگوله‌ای شکل (Bell Shaped Function)

در حقیقت تمامی توابع زنگوله‌ای شکل برای توزیع نقاط روی خط قابل استفاده می‌باشد. به نظر می‌رسد نرم افزار Gambit از تابع منطق فازی برای توزیع دوطرفه المان‌های لبه استفاده می‌کند. به دلیل زیاد بودن این توابع تنها به ارسال لینک زیر اکتفا شده است.

https://en.wikipedia.org/wiki/Bell_shaped_function

 

تابع پوآسون

در این تابع نیز لازمست اندازه‌های اولین و آخرین المان را مشخص کنید تا با استفاده از معادلات (14) توزیع المان‌ها روی لبه مشخص شود. در این معادلات Sp₁ و Sp₂ به ترتیب طول اولین و آخرین المان (همان l₁ و l₂) هستند. تابع P(t) باید شرط مرزی نیومن را ارضاء کند که با استفاده از روش سعی و خطا به دست می‌آید.

 

سایر توابع توزیع دو طرفه

سایر توابع توزیع دو طرفع عبارتند از:

• توابعی مثل Biexponential، Bigeometric همان تعریف Exponential و Geometric را دارند که شبکه بندی خط را براساس تقسیم لبه به دو نیم لبه انجام می‌دهند.
• تابع توزیع براساس انحنای خط یا لبه (با اصطلاح Curvature) می‌باشد.
• رابطه خطی (Linear) که در آن توزیع نقاط خطی است.
• تابع Spline که با استفاده از معادله mspline نقاط را روی خطوط توزیع می‌کند.
• From Graph تابعی است که به صورت گرافیکی در نرم افزار ICEM-CFD برای توزیع نودها روی لبه تعریف می‌شود.

 

جدول-2: توابع مورد استفاده در توزیع دو طرفه المان‌ها روی لبه.