معادلات مشتقات جزئی بیضوی

Elliptic Partial Differential Equations

معادلات مشتقات جزئی بیضوی یکی از سه دسته مهم معادلات مشتقات جزئی به شمار می‌روند. تعداد بسیاری از مسائل مهم علمی نظیر توزیع دائمی دما در یک جسم جامد و جریان پتانسیل (جریان تراکم‌ناپذیر غیر چرخشی) در قالب یک معادله مشتق جزئی بیضوی ساده تعریف می‌شوند. البته معادلات ناویر-استوکس تراکم ناپذیر و پایا نیز نمونه پیچیده‌ای از دستگاه معادلات بیضوی بشمار می‌رود که ترم لزجت منشاء رفتارهای بیضی گونه این معادلات است.

در سیستم معادلات مشتقات جزئی بیضوی هیچ‌گونه جهت مشخصه‌ای وجود نداشته و رفتار آن متعادل است. از آنجا که زمان در سیستم معادلات بیضوی جایی ندارد، برای حل این سیستم معادلات می‌توان یک از دو روش زمان مجازی(Artificial Time) که کمک می‌کند از روش‌های ساده‌تری معروف به روش‌های صریح استفاده کرد و یا یکی از روش‌های تکرار را بکار برد. در این نوشته حل تحلیلی و عددی معادلات دیفرانسیل جزئی بیضوی مورد بحث و بررسی قرار گرفته است.

معادلات لاپلاس و پوآسون (Laplace and Poisson Equations)

معادله لاپلاس دوبعدی ساده‌ترین نوع معادله دیفرانسیل جزئی بیضوی (معادله 1) است. همچنین، فرم غیر همگن آن (معادله پواسون) که در بسیاری از مسائل فیزیکی کاربرد دارد، بصورت معادله (2) تعریف می‌شود.

حل تحلیلی معادلات دیفرانسیل جزئی بیضوی

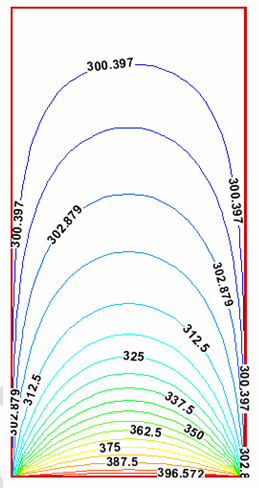
همانند معادله موج برای حل تحلیلی معادله لاپلاس نیز می‌توان از روش جداسازی متغیرها استفاده کرد. بمنظور مقایسه بین حل‌های تحلیلی و عددی، به عنوان یک مثال مشترک معادله (1) با شرط مرزی مندرج در معادله (3) مورد بررسی قرار می‌گیرد. برای حل این مسئله با استفاده از روش جداسازی متغیرها معادله (4) فرض می شود. با جایگذاری معادله (4) در معادله لاپلاس، معادله (5) نتیجه می‌دهد. رابطه (6) نیز به راحتی از رابطه (5) استخراج می‌شود.

از آنجاکه سمت چپ معادله (6) تنها تابعی از x و سمت راست آن تنها تابعی از y می‌باشد، لذا این دو ترم باید برابر یک مقدار ثابت باشند. بنابراین معادله (7) بدست می‌آید. در این رابطه، a یک عدد حقیقی است. در نتیجه حل نهایی برای توابع X و Y بصورت معادلات (8) و (9) هستند. که در این دو معادله، A, B, C & D ثابت هستند.

از آنجائیکه معادله لاپلاس یک معادله خطی است، حل عمومی ترکیب خطی از جوابهای فوق خواهد بود. برای مثال فوق لازمست که شرائط مرزی نیز مشخص شود. بعنوان مثال، اگر u روی مرزها صفر باشد. در x=0 و x=L ، باید X=0 و در y=0 نیز Y برابر صفر باشد. با توجه به این موضوع لازمست که عبارت‌های B=0، C+D=0 و A SinaL=0 برقرار باشد. برای حل غیر بدیهی، A≠0 و بنابراین SinaL=0 است. این مهم زمانی اتفاق می‌افتد که رابطه (10) برقرار باشد. در رابطه مذکور، n یک عدد صحیح مثبت است. با جایگذاری رابطه فوق در معادلات (8)، (9) و (4) جواب نهایی بصورت معادله (11) بازنویسی می‌شود. همچنین با استفاده از شرط مرزی u=1 روی y=L ، ضرائب A_n طبق رابطه (12) بدست می‌آید.