پردازش نزدیک دیواره منتر- لچنر (Menter-Lechner Near-Wall Treatment)

پردازش نزدیک دیواره منتر- لچنر

Menter-Lechner Near-Wall Treatment

پردازش نزدیک دیواره منتر- لچنر (Menter-Lechner Near-Wall Treatment) به عنوان جایگزینی برای تقریب دولایه توسعه یافته است. در این مطلب قصد داریم تا این پردازشگر را به تفصیل توضیح دهیم. قبل از هر چیز و جهت یادآوری می‌توان گفت که از لحاظ تاریخی دو رویکرد برای مدلسازی جریان نزدیک به دیواره وجود دارد که عبارتند از:

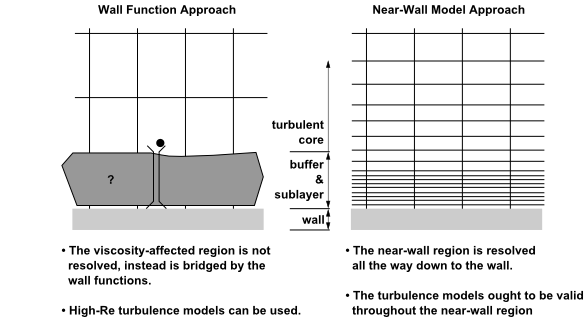
رویکرد تابع دیواره (Wall Function)
مدل (فرمولاسیون) عدد رینولدز پایین (Low-Reynolds Number Model)

توابع دیواره نیاز دارند که مرکز اولین ردیف المان چسبیده به دیواره در لایه لگاریتمی (کاملا آشفته) قرار گیرد. در حالیکه فرمولاسیون عدد رینولدز پایین نیاز دارد که شبکه تا اندازه‌ای ریز باشد که y⁺<1 باشد.

هر دو رویکرد در صورتیکه ورای دامنه عملکرد خود قرار گیرند، خطاهای بزرگی تولید خواهند کرد. روش تابع دیواره با ریز شدن شبکه کارایی خود را از دست می‌دهد در حالیکه نتایج فرمولاسیون عدد رینولدز پایین مرتبط با تنش برشی دیواره و انتقال حرارت برای شبکه‌بندی که در آن ⁺y کمی بزرگتر از 1 شود، غیر دقیق خواهد بود.

به منظور ارائه روابطی با حساسیت کمتر به کاربران CFD، مدل‌های دیواره‌‌ی توسعه یافته‌اند که حساسیت کمتری نسبت به ⁺y دارند. به این معنی که مقادیر دیواره محاسبه شده (تنش برشی و انتقال حرارت) استقلال خوبی از ⁺y بدست آمده از تولید شبکه دارند. هر پردازش دیواره غیر حساس به ⁺y در صورت ریز بودن شبکه و ⁺y پایین، از مدل رینولدز پایین و در صورت درشت بودن شبکه و ⁺y بالا از فرمولاسیون توابع دیواره استفاده می‌کند. یکی از محدودیت‌های اصلی این روش پردازش دیواره برای ε اینست که هیچ مدلسازی رینولدز پایین مناسبی برای آن در دسترس نیست. با وجود اینکه بسیاری از این نوع مدل‌ها توسعه یافته و منتشر شده‌اند، اما هرکدام از آن‌ها از یک یا چند تا از مشکلات زیر رنج می‌برند:

فرمولاسیون پیچیده‌ و شامل تعداد زیادی ترم‌های میرایی غیر خطی است.
فرمولاسیون برای جریان‌های پیچیده با ثبات (Robust) نیست.
فرمولاسیون برای یک مسئله خاص چندین پاسخ متفاوت تولید می‌کند.
فرمولاسیون نتایج شبه گذرا (Pseudo-Transitional) تولید می‌کند (این یعنی نواحی آرام غیر فیزیکی).

بخاطر موانع بالاست که در حال حاضر نرم افزارهای تجاری-صنعتی از فرمولاسیون معروف به دولایه برای معادله ε استفاده می‌کنند. با این فرمولاسیون از حل معادله ε در زیر لایه لزج صرف‌نظر شده و بجای آن از یک رابطه جبری مبتنی بر یک مدل طول تداخل ساده استفاده می‌شود.

در نرم افزار Fluent، مدل دولایه، پایه و اساس پردازش دیواره پیشرفته به شمار می‌رود که یک فرمولاسیون مستقل از ⁺y برای تمامی مدل‌های آشفتگی ε می‌باشد. در رویکرد دولایه، دامنه‌ی سیال به دو ناحیه تحت تأثیر لزجت و کاملا آشفته تقسیم‌بندی می‌شود. ترکیب این دو ناحیه با استفاده از عدد رینولدز آشفته (اینجا) صورت می‌پذیرد. به هر صورت استفاده از عدد رینولدز آشفته Re_y برای تعیین رژیم جریان با اشکالاتی نیز همراه است که مهمترین‌ آن‌ها عبارتند از:

نواحی همراه با مقادیر کمی از انرژی جنبشی آشفتگی ممکن است دارای عدد رینولدز آشفته کمتر از 200 باشند. بنابراین، این نواحی با استفاده از مدلسازی نزدیک دیواره تحلیل می‌شوند حتی اگر فاصله قابل توجهی تا دیواره داشته باشند (به عنوان مثال نواحی همراه با سطح آشفتگی بسیار پایین).
در جریان‌های نامتعادل (همراه با گرادیان فشار) مدل ولفشتاین با معادله ε سازگار نیست. بنابراین برای حل ترکیبی به مکان سوئیچ کردن (مرز بین ناحیه تحت تأثیر لزجت و ناحیه کاملا آشفته) نیاز است.
برای یک شبکه درشت با ⁺y بزرگ در المان مجاور دیواره در نزدیکی مکان سوئیچ کردن مدل دولایه به نوسان کردن تمایل دارد. به این مفهوم که در بین گام‌های زمانی (یا تکرار) بین دو ناحیه تحت تأثیر لزجت و کاملا آشفته سوئیچ می‌کند. این نوسانات از همگرایی حل جلوگیری می‌کنند.

پردازش نزدیک دیواره منتر-لچنر:

برای پرهیز از این مشکلات پردازش نزدیک دیواره منتر-لچنر به عنوان فرمولاسیون جایگزینی که مبتنی بر تقریب دولایه نیست توسعه یافته است. این پردازشگر همچنین از یک فرمولاسیون عدد رینولدز پایین k-ε بهره می‌برد. هدف از پردازش نزدیک دیواره غیر حساس به ⁺y پیش‌بینی مناسب و مستقل از ⁺y مقادیر تنش برشی دیواره و شار حرارتی (با فرض وضوح مناسب لایه مرزی) می‌باشد. این فرمولاسیون به تدریج از توابع دیواره به فرمولاسیون رینولدز پایین زمانیکه شبکه ریز می‌شود سوئیچ می‌کند. این مهم نیازمند ترکیب مقادیر متغیر در لایه ترکیبی بین زیر لایه لزج و ناحیه لگاریتمی می‌باشد.

معادله ممنتم در پردازش نزدیک دیواره منتر- لچنر (Menter-Lechner Near-Wall Treatment)

تنش برشی دیواره به عنوان یک شرط مرزی مورد نیاز است که با استفاده از معادله (1) تعیین می‌شود. در این معادله ρ چگالی است. ترکیب مقادیر بین زیر لایه لزج و ناحیه لگاریتمی برای سرعت‌های ^*u و u_τ با استفاده از روابط (2) و (3) صورت می‌گیرد.

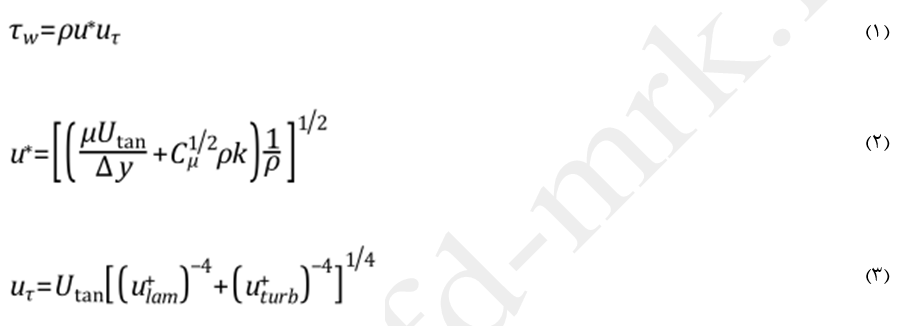
مدل‌های آشفتگی K-ε در پردازش نزدیک دیواره منتر- لچنر (Menter-Lechner Near-Wall Treatment)

ایده اصلی پردازش نزدیک دیواره منتر-لچنر افزودن یک ترم چشمه برای محاسبه اثرات نزدیک دیواره به معادلات انتقالی انرژی جنبشی آشفتگی، k، می‌باشد. در نتیجه مدل استاندارد k-ε طبق معادلات (4) و (5) اصلاح می‌شود. در این معادلات اثرات شناوری به دلیل سادگی نوشتار گنجانده نشده است.

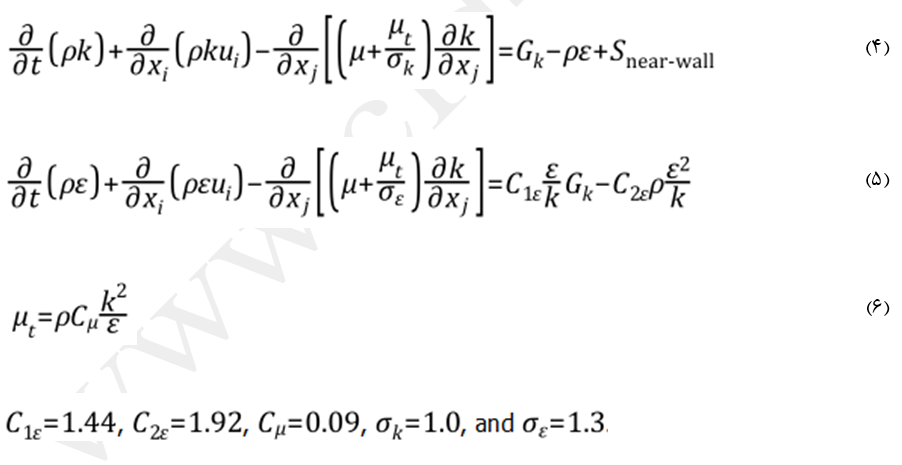
ترم چشمه اضافی Snear-wall تنها در زیرلایه لزج فعال بوده و برای تعیین اثرات عدد رینولدز پایین بکار می‌رود. این ترم بطور خودکار در نواحی لگاریتمی صفر می‌شود.

بهبود تکرار

در ترکیب با پردازش نزدیک دیواره منتر-لچنر، حل تکراری و خطی سازی مدل دو معادله k-ε بهبود یافته است. پردازش نزدیک دیواره منتر-لچنر می‌تواند همراه با مدل‌های آشفتگی K-ε Standard; RNG & Realizable بکار گرفته شود.