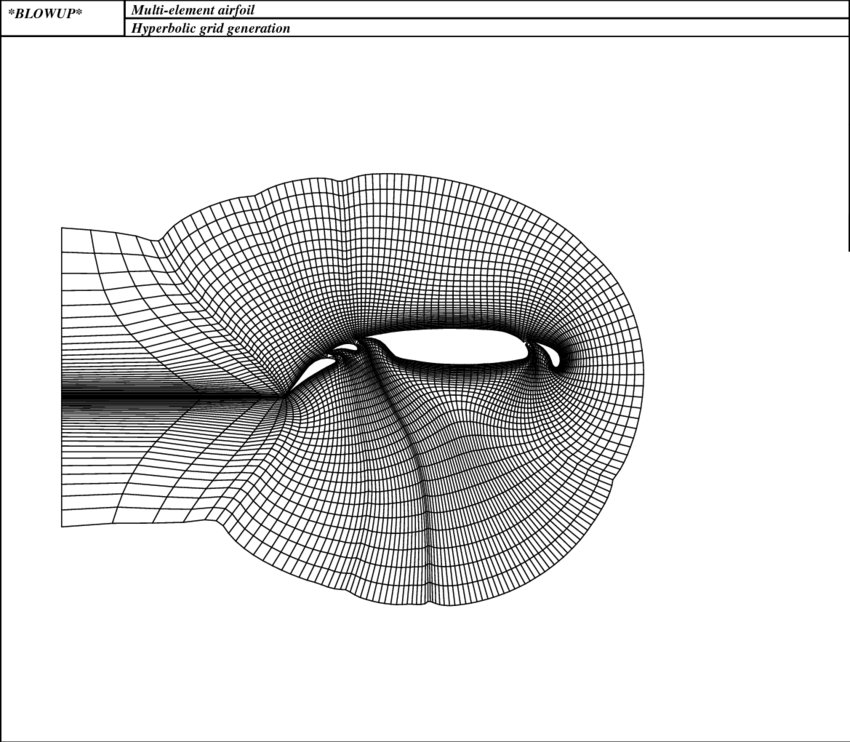
شبکه (مش) بندی باسازمان هذلولوی

شبکه(مش) بندی باسازمان هذلولوی

Hyperbolic Structured Mesh Generation

معمولاً از شبکه (مش) بندی باسازمان هذلولوی برای شبکه‌بندی برای قلمرو‌های بازی که در آن مرز خارجی را نمی‌توان مشخص کرد، استفاده می‌شود. از آنجا که برای شبکه بندی باسازمان بیضوی از روش گام زمانی باید استفاده کرد، محاسبات در این روش نسبت به روش بیضوی سریع‌تر است. عملیات ریاضی برای حل معادلات دیفرانسیل جزئی هذلولوی براساس دو فرض بنا می‌شود.

فرض اول:

در فرض اول تعامد خطوط شبکه در دامنه محاسباتی مطرح می‌باشد. بدیهی است که دو خط زمانی برهم عمود هستند که حاصل ضرب شیب‌های این دو خط (1-) باشد. طبق تعریف ریاضی شیب خطوط ξ و η ثابت طبق رابطه (78) محاسبه می‌شود. از انجائیکه در امتداد یک خط ξ ثابت، ξd برابر صفر است. لذا معادله (79) صادق است. بطور مشابه برای هم معادلات (80) و (81) استخراج می‌شود. با اعمال شرط تعامد معادلات (82) تا (84) حاکم خواهد بود. در نهایت با استفاده از تبدیل متریک‌ها و ژاکوبین‌ها معادله (84) به صورت معادله (85) بازنویسی می‌شود.

فرض دوم:

فرض دوم مربوط به چند نکته هندسی است. برای رسیدن به این هدف، دو روش مورد بررسی قرار می‌گیرد. در روش اول ژاکوبین تبدیل معرفی می‌شود. متدهای متعددی برای تعریف این پارامتر وجود دارد که در ادامه بحث می‌شود. متد اول با عنوان روش مساحت سلول شناخته می‌شود. در متد دوم، طول قوس از یک نقطه شبکه تا نقطه بعدی مشخص می‌شود. این متد به متد طول قوس (Arc Length) معروف است.

روش مساحت سلول

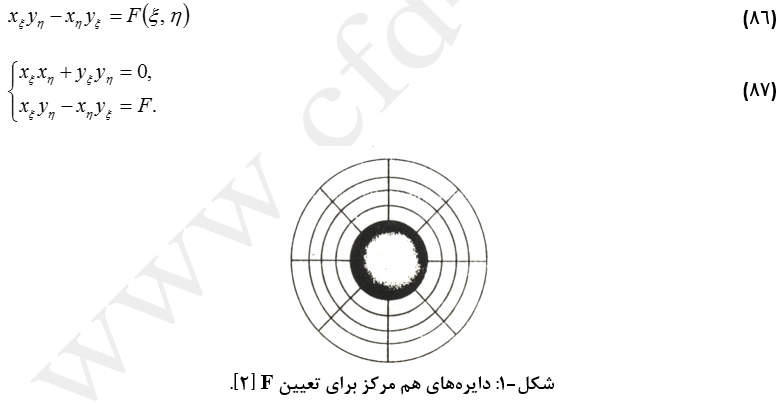
در روش مساحت سلول، از تعریف ژاکوبین تبدیل به عنوان دومین معادله هذلولوی استفاده می‌شود که به صورت معادله (86) می‌باشد. دستگاه معادلات هذلولوی (87) برای تعیین توزیع نقاط در فضای فیزیکی حل می‌شود. برای حل این دستگاه معادلات، لازمست F معلوم باشد و می‌توان آن را با استفاده از روش‌های مختلفی تعیین کرد. اولاً، برای بیان توزیع F(ξ, η) از دایره‌های هم‌ مرکز استفاده می‌شود. برای انجام این کار، دایره‌هایی تعریف می‌شود که محیط آن برابر مرز داخلی قلمرو فیزیکی است. سپس، چند دایره هم مرکز با شعاع‌های مختلف تعریف می‌شود. برای تعیین این دایره‌ها می‌توان از روابط جبری استفاده نمود (همانند روش بکار رفته در متراکم‌سازی شبکه خطوط). پس از، آن گره‌های شبکه روی دایره داخلی (مرز جسم) توزیع شده و در ادامه گره‌های محاسباتی روی سایر دایره‌ها با شعاع‌های رسم شده از مرکز آن‌ها را تعیین می‌کنیم (شکل-1).

باید توجه داشت که برای تعریف دایره‌های هم مرکز می‌توان از روش‌های متراکم‌سازی برای خطوط شبکه نیز استفاده کرد.

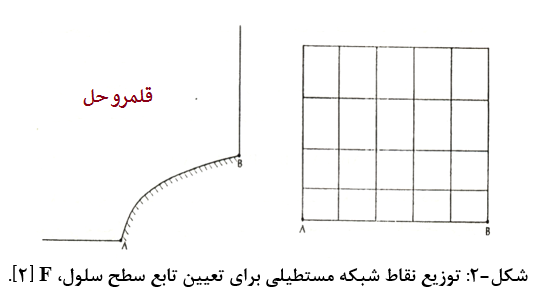
در روش دوم، طول مرز داخلی به صورت یک خط مستقیم با همان توزیع نقاط مشخص می‌شود. سپس، خطوط شبکه موازی (η ثابت) ایجاد می‌شود تا شبکه غیر یکنواخت در قلمروی مستطیلی تولید شود. تراکم شبکه در این اینجا نیز اعمال می‌شود. در این مرحله ژاکوبین محاسبه شده تا تابع F مشخص شود (شکل-2).

در روش سوم از یک شبکه جبری برای تعیین تابع سطح سلول استفاده می‌شود. این روش بسیار منسجم‌تر از دو روش قبلی بوده و ایجاد تراکم در خطوط این شبکه نیز آسان‌تر است.

با تعیین تابع F نوبت به حل دستگاه معادلات (87) می‌رسد. نکته قابل توجه در دستگاه معادلات مذکور این است که یک دستگاه غیر خطی می‌باشد و برای حل آن باید از روش خطی سازی استفاده نمود. به عنوان نکته دوم، برای حل معادلات هذلولوی باید از روش زمان پیمایشی استفاده نمود. بنابراین، برای این فرمولاسیون، گام زمانی در جهت η خواهد بود. نکته سوم بیانگر این موضوع است که در حل دستگاه‌های هذلولوی، شرائط اولیه و مجموعه‌ای از شرائط مرزی باید مشخص شود. در نهایت، برای جلوگیری از بروز نوسانات در جواب، لازمست که یک ترم استهلاکی از مرتبه چهار به طرف راست معادلات اضافه شود.

برای خطی سازی معادلات از روش تکراری نیوتن استفاده می‌شود. دقت کنید یک عبارت جبری غیر خطی به صورت معادله (88) تقریب زده می‌شود که در آن، k گام زمانی قبلی است (در ادامه بالانویس k+1 در معادلات حذف شده است.) بنابراین، متغیر‌هایی که هیچ‌گونه بالانویسی ندارند، متغیرهای نامعلوم در گام زمانی k+1 شناخته می‌شوند. با توجه به این توضیحات، خطی سازی دستگاه معادلات هذلولوی (87) طبق دستگاه معادلات (89) خواهد بود. از دستگاه معادلات (87) معادله (90) نتیجه‌گیری می‌شود. با استفاده از معادلات (90)، دستگاه معادلات (89) به صورت زیر معادلات (91) ساده می‌شود. فرم فشرده دستگاه معادلات (91) به صورت معادله ماتریسی (92) است.

روش طول قوس

در روش طول قوس، در دستگاه معادلات بیضوی، اولین معادله شبیه به روش سطح سلول است. به عبارت دیگر معادله براساس شرط تعامد خطوط شبکه به دست می‌آید (رابطه 93). از طرفی، شرط هندسی طبق رابطه (94) برقرار می‌باشد. با معکوس کردن متغیرهای مستقل x و y شرط فوق به صورت معادله (95) تغییر می‌کند. اگر Δξ=Δη=1 در نظر گرفته شود آنگاه به معادله (96) می‌رسیم.

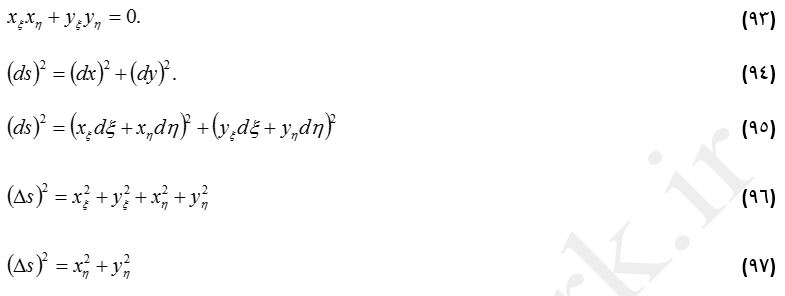
مقدار Δs به عنوان ورودی مشخص می‌شود و توزیع آن را می‌توان برای تراکم‌سازی شبکه استفاده کرد. از حل دستگاه معادلات هذلولوی (93) و (96) شبکه گره‌های محاسباتی به دست می‌آید. در استفاده از این فرم دستگاه معادلات مشکلاتی وجود دارد که برای حل آن Δs در امتداد یک خط ξ ثابت در نظر گرفته می‌شود. در نتیجه، معادله (96) به صورت معادله (97) خلاصه می‌شود. دستگاه معادلات (93) و (97) را می‌توان به راحتی حل کرد.

با توجه به مطالب عنوان شده، در یک جمع بندی کلی فواید شبکه بندی به روش دیفرانسیلی هذلولوی عبارتند از:

تعامد شبکه در حالت دو بعدی،
سریع بودن روش (نسبت به روش بیضوی) و
کنترل پذیری اندازه المان‌های شبکه.

از طرفی روش یاد شده معایبی نیز دارد که مهمترین آن‌ها از قرار زیر است:

این روش را نمی‌توان به حالت سه بعدی تعمیم داد،
برای قلمرو‌هایی که مرز خارجی آن تعریف شده باشد قابل استفاده نیست،
شرائط مرزی قابل انتشار به داخل قلمرو است و
توابع سطح سلول و یا طول قوس لازمست دقیق معرفی شوند. در غیر این صورت، این توابع باعث ایجاد شبکه‌ای نامطلوب می‌شود.

https://www.researchgate.net/figure/Mono-block-grid-generated-with-a-hyperbolic-method-about-a-multi-element-airfoil_fig3_237791571