خوردگی دیواره (Wall Erosion)

خوردگی دیواره

Wall Erosion

خوردگی دیواره (Wall Erosion) فرآیندی است که مواد تشکیل دهنده دیواره به تدریج و به دلیل تغییر شکل میکرومکانیکی، خراشیدگی یا ترک خوردگی سطح دیواره از آن خارج می‌شوند. در تجهیزات حمال مایعات (مانند توربین‌های گازی و آبی، انواع پمپ‌ها، مبدل‌های حرارتی و سایر موارد) خوردگی سطحی، ناشی از کاویتاسیون یا برخورد ذرات جامد در جریان سیال بر روی دیواره آن‌ها می‌باشد. لازم به توضیح است که در این پست، بحث بررسی اثر برخورد ذرات جامد موجود در سیال به سطح دیواره مد نظر است. نکته مهم دیگر اینکه فرسایش یا خوردگی دیواره موجب تخریب تجهیزات و در نتیجه کاهش طول عمر مفید و عملکرد آن‌ها می‌شود.

مقاومت ماده دیواره در برابر فرسایش به قابلیت انعطاف پذیری آن تحت ضربه همراه با سایر پارامترهای فهرست شده در ادامه بستگی دارد. در مواد شکننده، فرسایش و خوردگی در نتیجه ترک خوردن و خرد شدن دیوار در ابعاد بسیار ریز در سطح خودش اتفاق می‌افتد. در حالیکه اگر دیواره از جنس یک ماده انعطاف‌پذیر باشد، فرسایش بخاطر خستگی ناشی از تغییر شکل‌های کوچک، مداوم و پلاستیک رخ می‌دهد. برای چنین مواردی معمولا در زوایای برخورد 20 تا 30 درجه، بیشترین میزان خوردگی اتفاق میافتد. سایر پارامترهای موثر در فرسایش دیواره عبارتند از:

• سرعت برخورد ذره
• زاویه برخورد ذره
• خواص مکانیکی جنس دیواره (به عنوان مثال شامل فناوری ساخت، مشخصه‌های میکرو مکانیکی و غیره)
• ضریب اصطکاک بین ذره و دیواره
• اثرات محافظتی (پوششی) سطح به دلیل برگشت ذرات پس از برخورد با سایر ذرات عبوری از نزدیک دیواره

معمولا نتایج تجربی موجود برای فرسایش و خوردگی عدم قطعیت‌های زیادی داشته و خیلی نمی‌توان به آن‌ها تکیه کرد. در برخی موارد تفاوت نرخ خوردگی گزارش شده توسط محققان مختلف حتی برای یک ماده مشخص هم بسیار زیاد است. باید توجه داشت که نرخ‌های فرسایش محاسبه شده در مدل‎های خوردگی Fluent تنها یک رابطه کیفی برای بررسی پدیده فرسایش و خوردگی می‌باشد. مگر اینکه مقادیر بسیار دقیقی برای ثابت‌های مدل تعیین شود.

مدل‌های زیر برای پیش‌بینی گسترش و تعیین حجم خوردگی در نرم افزار Fluent قابل دسترسی است.

• مدل خوردگی فینی (Finnie)
• مدل خوردگی اوکا (OKA)
• مدل خوردگی مک لوری (McLaury)
• مدلسازی نرخ‌های خوردگی در جریان‌های چگال
• انباشتگی (Accretion)

مدل خوردگی فینی (Finnie Erosion Model)

تقریبا برای تمامی مواد شکل‌پذیر، فرسایش به صورت تابعی از سرعت و زاویه برخورد و طبق معادله (311) تغییر می‌کند. برای فلزات مقدار توان n معمولا بین 2.3 تا 2.5 رادیان تغییر می‌کند. مدل فینی میزان خوردگی را براساس نرخ جنبشی ضربه ذرات روی سطح و با استفاده از معادله (312) مشخص می‌کند.

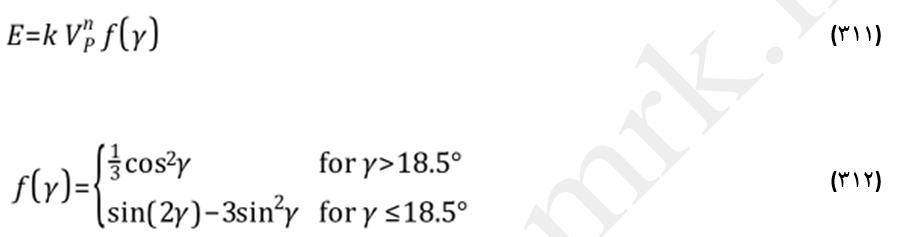
E: جرم بدون بعد خوردگی

k: ثابت مدل

Vp: سرعت برخورد ذره

f(γ): تابع بدون بعد زاویه برخورد γ

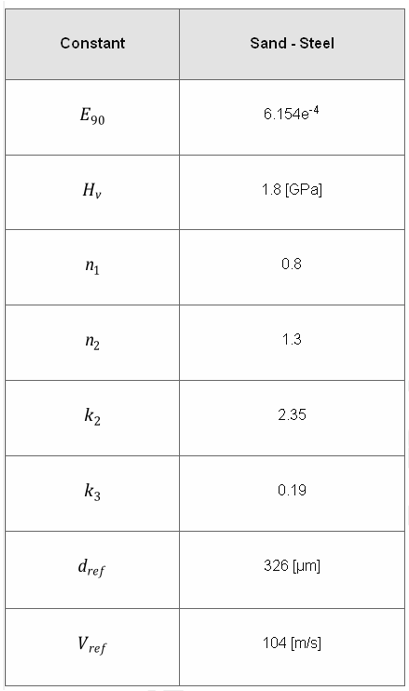
ثابت‌های پیش فرض مدل فرسایش فینی در نرم افزار فلوئنت تنها برای محاسبه خوردگی ناشی از برخورد ذرات ماسه با دیواره‌های فولاد کربنی صحیح می‌باشد. مقدار ثابت k از نتایج تجربی برگرفته از برخورد ذرات ماسه‌ای 326 میکرونی به یک دیواره فولاد کربنی در سرعت 104 متر بر ثانیه استخراج شده است. بنابراین بدیهی است که تنها تحت این شرایط می‌توان به ثابت مدل فینی اعتماد کرد.

مدل خوردگی اوکا (Oka Erosion Model)

با استفاده از مدل فرسایش اوکا در نرم افزار Fluent، جرم خوردگی بدون بعد  Eاز رابطه (313) بدست می‌آید.

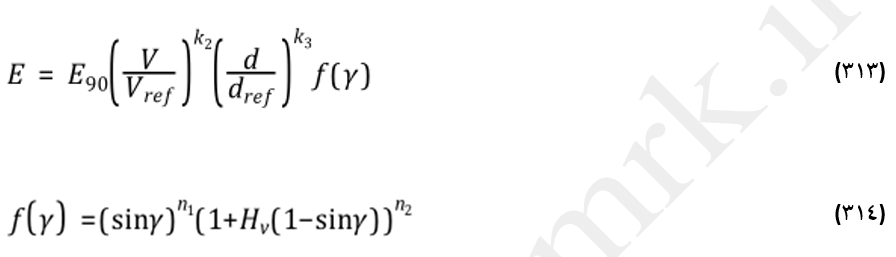
E₉₀: نرخ خوردگی در زاویه برخورد 90 درجه (این مقدار همیشه از طریق اندازه گیری معین می‌شود)

V: سرعت برخورد ذره

V_ref: سرعت مرجع

d و d_ref: قطر و قطر مرجع ذره

k2 و k3: به ترتیب بیانگر توان‌های سرعت و قطر

f(γ): تابع بدون بعد زاویه برخورد γ (معادله 314)

γ: زاویه برخورد دیواره (rad)

Hv: سختی ویکرز (Vickers hardness) جنس دیواره (GPa)

n1 و n2: ثوابت تابع زاویه

جدول-1: ثابت‌های مدل فرسایش اوکا (OKA)

 

مدل خوردگی مک‌لاری (McLaury Erosion Model)

مک‌لاری مدلی را برای پیش‌بینی نرخ خوردگی ناشی از ذرات ماسه در آب ارائه داد [1]. اساسا این مدل برای شبیه سازی نرخ فرسایش در خوردگی جریان دوغابی استفاده می‌شود. نرخ خوردگ مک‌لاری، E، با استفاده از معادله (315) محاسبه می‌شود.

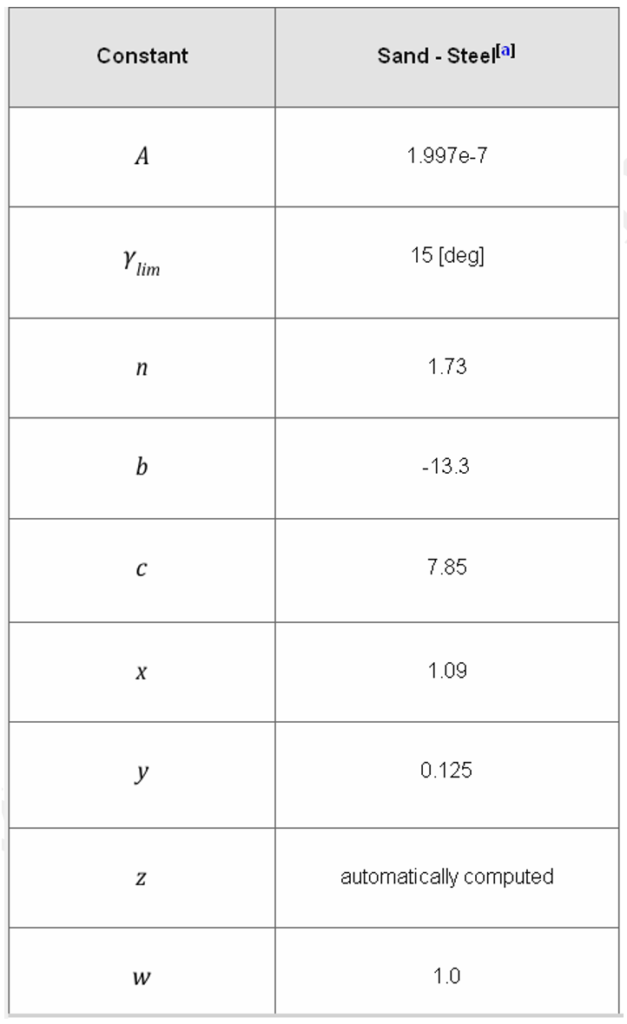
در معادلات فوق F: ثابت تجربی،

V: سرعت برخورد ذره،

Bh: عدد سختی برینل (Brinell’s Hardness) و 

K=-0.59 برای فولاد کربنی است که برای سایر مواد مقداری متفاوت دارد.

ثابت‌های b، c، w، x و y باید بصورت تجربی تعیین شوند. مقدار z نیز باید به گونه‌ای باشد که توابع زوایای معادلات (316) و (317) در  γ=γminبا یکدیگر منطبق باشد. γmin زاویه انتقال است.

ثوابت این مدل تنها برای مخلوط آب و ماسه مناسب هستند. سرعت‌های برخورد ذره در دامنه صفر تا 10 متر بر ثانیه فرض می‌شود.

جدول-2: مثالی از ثابت‌های مدل مک‌لاری

 

مدلسازی خوردگی در جریان‌های چگال (Modeling Erosion Rates in Dense Flow)

در جریان‌های چگال ممکن است اندرکنش (Interaction) ذره-ذره بخاطر اثرات لایه محافظ نزدیک دیواره (به دلیل تراکم ذرات در آن نواحی)، ذرات جامد روی نرخ خوردگی تأثیر بگذارد. به علاوه، ذرات جامدی که تقریبا نزدیک دیواره حرکت می‌کنند می‌توانند همانند یک سنباده دیوار را بسایند. در نرم‌افزارهایی مانند فلوئنت نرخ خوردگی کل در جریان‌های چگال از رابطه (318) محاسبه می‌شود. در این معادله E_abrasive، نرخ خوردگی سایشی (Abrasive Erosion) با استفاده از معادله (319) محاسبه می‌شود. E_imp هم خوردگی ناشی از برخورد (Impact Erosion) یا همان خوردگی برخوردی را معرفی می‌کند. خوردگی برخوردی با استفاده از معادله (322) محاسبه می‌شود.

بطور کلی خوردگی‌های سایشی و برخوردگی تحت تأثیر شرایط زیر محاسبه می‌شوند:

• فاز DPM با گزینه فاز DPM با گزینه Erosion/Accretion فعال
• وجود حداقل یک فاز اویلر گسسته جامد ریز دانه (Granular)

در بسیاری از موارد خوردگی دیواره، ذرات تمایل دارند در رگه‌های نزدیک به دیواره متمرکز شوند. این مهم فرض اصلی و اساسی DPM رژیم جریان پراکنده را نقض می‌کند. برای شبیه سازی ذرات متراکم با روش لاگرانژی، لازمست اندرکنش ذره-ذره همچون جابجایی حجم ذرات لحاظ شود. این شبیه سازی با استفاده از روش DPM امکان‌پذیر اما بسیار هزینه‌بر است.

نرم افزار Fluent برای پرهیز از این هزینه از فاز اویلر پراکنده که محاسبات جابجایی حجم را در هر نوع اندرکنش بین فازی انجام می‌دهد، استفاده می‌کند. البته فرض بر این است که فاز اویلر پراکنده به اندازه کافی رفتار ذرات در نزدیکی دیواره را توصیف می‌کند. خوردگی تا حد زیادی از مقادیر فاز اویلری (همانند خوردگی برشی دیواره (Wall Shear Erosion)) محاسبه می‌شود. عملکرد محاسباتی خوردگی کلاسیک DPM پیشنهادی توسط مدل‌های فینی، اوکا و یا مک‌لاری بواسطه حضور لایه محافظ کاهش می‌یابد.

خوردگی سایشی ناشی از ذرات جامد (Abrasive Erosion Caused by Solid Particle)

خوردگی سایشی فاز جامد در نزدیکی دیواره بصورت تابعی از تنش برشی دیواره و سرعت نزدیک دیواره فاز جامد مدل می‌شود (معادله 319). برای جریان‌های چند فازی با N فاز جامد ریز دانه، نرخ خوردگی کلی ناشی از تنش دیواره با مجموع نرخ خوردگی هر فاز ریز دانه برابر است (رابطه 320).

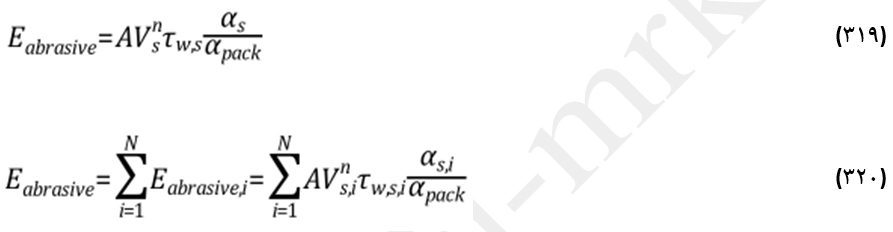
 در معادلات فوق A: ثابت تجربی،

Vs: سرعت فاز جامد،

n: توان سرعت

τ_w,s: تنش برشی دیواره فاز جامد،

α_s: کسر حجمی فاز جامد و

α_pack: حد پکینگ (0.63 برای ذرات کروی) هستند.

 

اثر محافظ دیواره در رژیم‌های جریان چگال (Wall Shielding Effect in Dense Flow Regimes )

در رژیم جریان چگال، ذرات نزدیک شونده به دیواره ساکن ممکن است توسط سایر ذرات که تقریبا موازی با دیواره حرکت می‌کنند، سرعتشان کاهش پیدا کرده و یا حتی برگشت داده شوند. این اثر محافظتی میزان خوردگی ناشی از برخورد ذرات بر سطح دیواره را بطور قابل توجهی کاهش می‌دهد. برای محاسبه این اثر از تابع محافظ نشان داده شده در معادله (321) استفاده می‌شود. از تابع محافظ، f_shield، برای تعیین نرخ خوردگی برخوردی هر فاز استفاده می‌شود. (معادله 322).

α_s: کسر حجمی فاز جامد و

α_pack: حد پکینگ (0.63 برای ذرات کروی) هستند.

اگر کسر حجمی محلی فاز جامد، α_s، به حد پکینگ، α_pack، نزدیک شود، آنگاه از سطح دیوار از هر گونه برخوردی محافظت می‌شود. به عبارت دیگر در این حالت نرخ کرنش برخورد، E_imp، صفر است. برای جریان‌های چند فازی با N فاز جامد ریز دانه، تابع محافظ از مجموع  کسرهای حجمی اویلری محاسبه می‌شود (رابطه 323).

 

انباشتگی (Accretion)

 

 

:[1]

. B. S. McLaury et al. “Modeling erosion in chokes”. Proceeding of ASME Fluids Eng. Summer Meeting. San Diego, California. 1996

 

 

https://www.alamy.com/rusted-white-painted-metal-wall-rusty-metal-background-with-streaks-of-rust-rust-stains-the-metal-surface-rusted-spotsmetal-rust-texture-image262024050.html