تئوری حرکت ذره در مدل DPM

Particle Motion Theory in DPM Model

تئوری حرکت ذره در مدل DPM براساس رهگیری تعداد زیادی از ذرات، حباب‌ها و یا قطرات بنا شده است. بنابراین پیش بینی حرکت ذرات در این مدل اهمیت حیاتی دارد. در همین راستا جزئیات تئوری حرکت ذره در DPM بطور کامل تشریح خواهد شد. این جزئیات در سه بخش معادلات حرکت، پراکندگی آشفتگی ذرات (Turbulent Dispersion of Particle) و انتگرال گیری معادله حرکت ذره (Integration of Particle Equation of Motion) بیان می‌گردد.

تئوری حرکت ذره در مدل DPM:

معادلات حرکت ذره

روابط حاکم بر حرکت ذرات از معادلات تعادل نیرو و گشتاور وارد بر ذرات تشکیل شده است. به دلیل عوامل متعدد خارجی این معادلات از تنوع زیادی برخوردار هستند. هدف ما معرفی این عوامل و چگونگی تأثیر آنها بر حرکت ذرات است.

تعادل نیرویی ذره

نرم افزارهایی مانند Fluent مسیر ذره، حباب و یا قطره را براساس برآیند نیروی وارد بر آن پیش بینی می‌کنند. این معادلات در فرم لاگرانژی نوشته می‌شود. در این تعادل نیرویی، اینرسی ذره معادل با نیرو‌های وارد بر آن در نظر گرفته می‌شود. با این توضیحات معادله تعادل نیرویی ذره بصورت رابطه (1) نوشته می‌شود.

تعادل گشتاوری ذره

دوران ذره به عنوان بخشی طبیعی از حرکت ذره بوده و می‌تواند تأثیر قابل توجهی بر مسیر حرکت ذره در سیال داشته باشد. این تأثیر حتی برای ذرات بزرگ و سنگین با اینرسی بالاتر می‌تواند برجسته‌تر باشد. برای محاسبه مقدار دوران ذره به حل یک معادله دیفرانسیل معمولی از جنس ODE برای گشتاور زاویه‌ای ذره نیاز است (معادله 2).

با توجه به معادله (4) مشهود است که بردار گشتاور T از اندرکنش بین اینرسی ذره و نیروی درگ آن ناشی می‌شود.

اعمال ترم جاذبه

موقعی که معادله (1) شامل نیروی جاذبه روی ذره نیز باشد لازمست که اثر جاذبه در نرم افزار Fluent لحاظ گردد چراکه طبق پیش فرض این نرم افزار، شتاب جاذبه صفر است. برای اعمال نیروی جاذبه باید مقدار و جهت صحیح آن در کادر محاوره‌ای شرایط عملیاتی (Operating Condition) تعریف شود.

سایر نیروها

در معادله (1) سایر نیروها توسط ترم نیروهای اضافی بردار F تعریف می‌شود. بسته به فیزیک جریان ممکن است نیروهای متفاوتی در ترم F تعریف شود. مثلا نیروی جرم مجازی (Virtual Mass) برای شتاب دادن سیال اطراف ذره الزامیست. این نیرو طبق رابطه (7) بیان می‌شود. نیروی اضافی دیگر از گرادیان فشار داخل سیال تولید شده و طبق رابطه (8) تعریف می‌شود.

نیروی جرم مجازی و گرادیان فشار در زمانیکه چگالی سیال به طور چشمگیری کمتر از چگالی ذره باشد، مهم نیستند. به عنوان مثال می‌توان به مسائل جریان گازی متشکل از ذرات جامد و مایع (قطرات) اشاره نمود. در صورتیکه مقدار نسبت چگالی سیال به ذره/قطره/حباب به سمت مقدار یک میل کند آنگاه نیروهای جرم مجازی و گرادیان فشار اهمیت پیدا می‌کند. پیشنهاد می‌شود که برای مقادیر ρ/ρ_p≥0.1 این ترم‌های نیرویی در محاسبات لحاظ گردند.

نیروها در دامنه‌های متحرک

ترم اضافی F^→ در معادله (1) می‌تواند معرف نیروهای ناشی از دوران دامنه محاسباتی روی ذره باشد. این نیروها در مدلسازی جریان در نواحی متحرک پدیدار می‌شوند. به عنوان مثال برای دوران یک ناحیه حول محور Z، نیروهای اعمالی بر ذره در مختصات کارتزین x و y را می‌توان بصورت معادلات (9) و (10) بیان نمود.

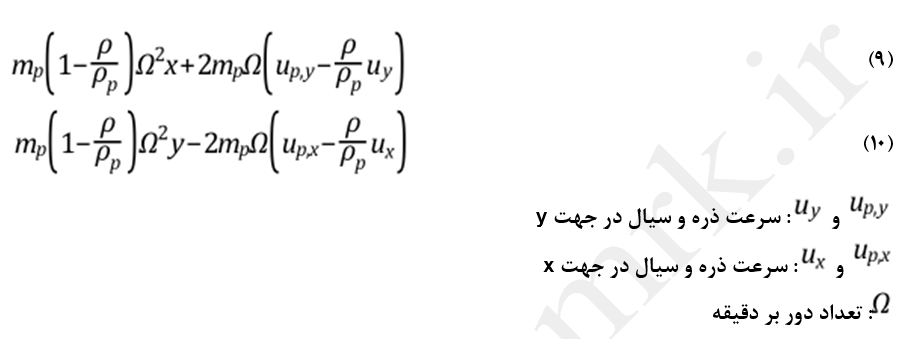
نیروی ترموفورتیک (Thermophoretic Force)

ذرات ریز احاطه شده در گاز که دارای دماهای متفاوتی هستند نیرویی در جهت عکس گرادیان دمایی را احساس می‌کنند. این پدیده به ترموفورزیز (Thermophoresis) مشهور است. در نرم افزار Fluent این قابلیت وجود دارد که اثر ترموفورتیک روی ذرات بصورت یک نیروی اضافی F در معادله (1) لحاظ گردد.در واقع نیروی ترموفورتیک بصورت معادله (11) تعریف شده و در ترم نیروهای اضافی F در معاده (1) اعمال می‌شود. در معادله زیر D_{T, P} ضریب ترموفورتیک است. این ضریب می‌تواند ثابت، چند جمله‌ای بوده و یا توسط کاربر تعریف شود. همچنین برای تعریف این ضریب می‌توان از معادله پیشنهادی تالبوت (Talbot) نشان داده شده در معاده (12) نیز استفاده نمود.

نیروی براون (Brownian Force)

برای ذرات با ابعاد کوچکتر از میکرون، اثرات حرکت براون (Brownian Motion) می‌تواند بطور دلخواه در ترم نیروی اضافی F در معادله (1) لحاظ گردد. مؤلفه‌های نیروی براون بصورت نویز سفید گوس (Gaussian White Noise) با شدت طیفی S_{n, ij} در قالب رابطه (13) مدلسازی می‌شود. رابطه (15) نیز دامنه مولفه‌های نیروی براون را مشخص می‌کند.

δij: تابع دلتای کرونکر

v: لزجت سینماتیکی

Cs: رابطه کانینگهام (Cunningham Correlation)

K_B: ثابت بولتزمن

ζi: عدد تصادفی گوس مستقل از تغییرات واحد و میانگین صفر است.

دامنه مؤلفه نیروی براون در هر گام زمانی رصد می‌شود. لازمست که معادله انرژی برای نیروی براون فعال گردد. نیروی براون تنها برای شبیه سازی جریان‌های آرام (Laminar) قابل استفاده است.

نیروی لیفت سافمن (Saffman’s Lift Force)

نیروی لیفت سافمن یا همان نیروی ناشی از برش را نیز می‌توان در صورت نیاز به عنوان یک نیروی اضفی در ترم F معاله (1) وارد کرد. در نرم افزار Fluent رابطه مورد استفاده برای محاسبه لیفت از تحقیق لی (Li) و احمدی (Ahmadi) اقتباس شده و به فرم عمومی رابطه سافمن ارائه می‌شود.

d_ij: تانسور تغییر شکل است.

اعمال نیروی سافمن تنها برای رینولدزهای پایین ذرات قابل استفاده است. تنها برای ذرات کوچکتر از میکرون در نظر گرفتن این نیرو پیشنهاد می‌شود.

نیروی لیفت مگنس (Magnus Lift Force)

نیروی لیفت مگنس یا نیروی لیفت دورانی در زمانیکه ذرات در داخل سیال دوار باشند، تولید و افزایش می‌یابد. این نیرو بخاطر اختلاف فشار روی سطح ذره ایجاد می‌شود. در شبیه سازی ذرات دوار، می‌توان نیروی مگنس را در قالب نیروی اضافی در ترم F معادله (1) اعمال نمود. برای اعداد رینولدز بالا نیروی مگنس FRL براساس ضریب لیفت دورانی، CRL، اندازه گیری می‌شود (معادله 17).

برای محاسبه ضریب نیروی دورانی، تقریب‌های مختلفی وجود دارد. در نرم افزار Fluent از سه مدل زیر برای محاسبه این پارامتر استفاده می‌شود:

الف: مدل اوسترل و بوئی‌دین (Oesterle and Bui Dinh)

در این مدل ضریب نیروی لیفت دورانی به دو پارامتر عدد رینولدز دورانی Rew و عدد رینولدز ذره وابسته است (رابطه 18)

ب: مدل تسوجی و همکاران (Tsuji et al)

ضریب نیروی لیفت دورانی بصور تابعی از پارامتر چرخش (Spin Parameter)، S، و براساس معادله (19) محاسبه می‌شود. این مدل بطور گسترده‌ای تا Rep<1600 مورد استفاده قرار می‌گیرد.

ج: مدل رابینو و کلر (Rubinow and Keller)

در مدل مذکور ضریب نیروی لیفت دورانی در قالب تابعی خطی از پارامتر چرخش، S، تعریف می‌شود (رابطه 21). این مدل می‌تواند به منظور مقایسه کردن یا مسائل آکادمیک مورد استفاده قرار کیرد.

تئوری حرکت ذره در مدل DPM:

پراکندگی آشفته ذرات (Turbulent Dispersion of Particles)

پراکندگی ذرات در اثر آشفتگی جریان سیال را می‌توان با استفاده از مدل‌های رصد تصادفی یا ابر ذرات پیش بینی نمود. مدل رصد تصادفی شامل تأثیر نوسانات لحظه‌ای سرعت آشفته روی مسیر جریان با استفاده از روش‌ها تصادفی می‌باشد. مدل ابر ذرات انتشار آماری ابر ذرات در امتداد یک مسیر میانگین را ردیابی می‌کند. میزان تمرکز ذرات در داخل ابر نیز با استفاده از تابع چگالی احتمالی گوس (Gaussian Probability Density Function) حول یک مسیر میانگین تعیین می‌گردد. برای مدل رصد تصادفی نیز یک مدل جداگانه برای محاسبه تولید یا اتلاف آشفتگی در فاز پیوسته در دسترس است.

مدل رصد تصادفی (Stochastic Tracking)

در جریان‌های آشفته نرم افزارهایی مانند Fluent مسیر ذرات را با استفاده از سرعت متوسط فاز سیال در معادله (1) پیش بینی می‌کند. البته شما مختارید که مقدار لحظه‌ای نوسانات سرعت جریان گاز را هم برای تخمین پراکندگی ذرات در اثر آشفتگی در نظر بگیرید (رابطه 22).

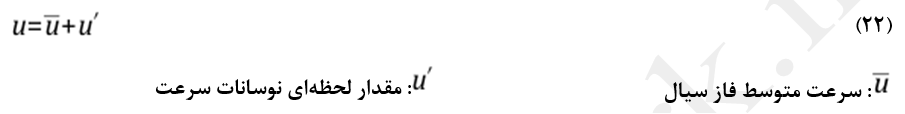
در رویکرد تصادفی، نرم افزار Fluent پراکندگی آشفته ذرات را با انتگرال گیری معادله مسیر برای هر ذره با استفاده از سرعت لحظه‌ای ذرات و در امتداد مسیر ذره پیش بینی می‌کند. در این روش با محاسبه مسیر برای تعداد مشخصی از ذرات، اثرات اتفاقی آشفتگی روی ذره لحاظ می‌گردد. این نرم افزار از روش رصد تصادفی یا همان مدل حرکت اتفاقی (Discrete Random Walk Model) برای اندازه‌گیری سرعت لحظه‌ای گاز استفاده می‌کند. در مدل حرکت اتفاقی (DRW)، مؤلفه‌های نوسانی سرعت بصورت توابع ثابت تکه‌ای (Piecewise Constant Functions) از زمان هستند. مقادیر تصادفی آن‌ها در طی زمان تسخیر شده توسط مشخصه طول عمر گردابه‌ها ثابت نگه داشته می‌شود.

ممکن است مدل DRW در جریان‌های به شدت غیر خطی پاسخ‌های غیر فیزیکی بدهد. مثلا جائیکه ذرات کوچک باید بصورت یکنواخت توزیع شوند. در عوض این مدل به شبیه سازی ذرات متمرکز در مناطق با آشفتگی کم روی خوش نشان می‌دهد. علاوه بر این مشهور است که این مدل به خاطر آشفتگی پیش بینی ضعیفی از نرخ تأثیر دیواره روی حرکت ذرات با قطر کمتر از چند میکرون می‌دهد.

زمان انتگرال (The Integral Time)

پیش بینی پراکندگی ذرات از مفهوم مقیاس زمان انتگرال (معادله 23) استفاده می‌کند. زمان انتگرال متناسب با میزان پراکندگی ذرات است. مقادیر بزرگتر مبین حرکت آشفته‌تر در جریان است. می‌توان نشان داد که انتشار ذرات همان می‌باشد. برای ذرات کوچک معروف به ردیاب Tracer که با سیال حرکت می‌کنند (سرعت دریفت صفر است) زمان انتگرال می‌تواند همان زمان انتگرال لاگرانژی سیال، T_L باشد که با استفاده از رابطه (24) تخمین زده می‌شود. از آنجائیکه مقدار C_L مشخص نیست بنابراین لازمست تعیین شود.

با تطبیق انتشار ذرات ردیاب، ، و نرخ انتشار اسکالر تخمینی νt/σ توسط انواع مدل‌های K-Ɛ، می‌توان از معادله (25) استفاده نمود. اما اگر از مدل RSM برای شبیه سازی جریان‌های آشفته استفاده شود، آنگاه معادله (26) توصیه می‌گردد. در حالت استفاده از مدل‌های K-ω، با جایگذاری Ɛ=0.09kω در معادله (24) مقدار T_L محاسبه ی‌گردد. در LES نیز از مقیاس زمانی LES استفاه می‌شود.

مدل حرکت اتفاقی گسسته (Discrete Random Walk Model)

مدل حرکت اتفاقی (DRW) یا همان مدل طول عمر گردابه (Eddy Lifetime) اندرکنش یک ذره با گردابه‌های آشفتگی فاز مایع فاز مایع گسسته شبیه سازی شده است. مشخه هر گردابه عبارتند از:

توزیع گوسی نوسانات تصادفی سرعت: ‘u ‘ v و ‘w
اندازه زمانی: Ʈ_e

با فرض پیروی از توزیع احتمالی گوسی، مقادیر u’، v’ و w’ غالب در طول عمر گردابه آشفته نمونه برداری می‌شوند (رابطه 27). که ζ یک عدد تصادفی و سایر پارامترهای سمت راست معادله (27) مقدار RMS محلی نوسانات سرعت هستند.

بخاطر معلوم بودن انرژی آشفتگی در هر نقطه از جریان، مقادیر مؤلفه‌های نوسانات سرعت (با فرض ایزوتروپی) برای انواع مدل‌های K-Ɛ و K-ω بصورت رابطه (28) تعریف می‌شوند. درصورت استفاده از مدل RSM در رابطه با قاب مرجع که در آن ممان دوم آشفتگی قطری است، غیر همسانی تنش‌ها در تعیین مقادیر نوسانات سرعت لحاظ می‌گردد (روابط 29 تا 31).

تئوری حرکت ذره:

در مدل LES نوسانات سرعت در تمام جهات معادل هم هستند. طول عمر مشخصه می‌تواند ثابت باشد (رابطه 32) که در آن T_L معمولا از رابطه (24) اقتباس گشته یا یک متغیر تصادفی نردیک به T_L باشد (معادله 33). در این معادله r عدد تصادفی یکنواخت بزرگتر از صفر و کوچکتر از یک است. T_L نیز از رابطه (25) گرفته می‌شود. قابل توجه است گزینه محاسبه تصادفی Ʈ_e توزیع واقع بینانه‌تری از تابع تصحیح ارائه می‌دهد. زمان گذر گردابه بصورت معادله (34) تعریف می‌شود.

فرض اندرکنش ذره با گردابه فاز سیال روی مقدار کمتر بین پارامترهای طول عمر و زمان گذر گردابه لحاظ می‌گردد. با اتمام این زمان، مقدار جدیدی برای سرعت محاسبه شده و در مقدار ζ در معادله (27) بکار گرفته می‌شود.

باید توجه داشت در نرم افزار Fluent مقدار ثابت مقیاس زمانی انتگرال، C_L (همان مقدار T_L یا Ʈ_e در معادلات 24 یا 32) و همچنین انتخاب روش مورد استفاده برای پیش بینی طول عمر گردابه، تنها ورودی‌های مورد نیاز برای مدل DRW هستند. شما مختارید که در هر تزریق یک مقدار ثابت و یا تصادفی برای C_L انتخاب کنید. این تنظیمات در کادر محاوره‌ای Injection Properties در نرم افزار مذکور انجام می‌شود.

رصد ابر ذره (Particle Cloud Tracking)

پراکندگی ذرات در اثر نوسانات آشفته را با مدل ابر ذرات نیز می‌توان شبیه سازی کرد. پراکندگی آششفته ذرات حول یک مسیر میانگین با استفاده از روش‌های آماری محاسبه می‌شود. تمرکز ذرات حول این مسیر متوسط با استفاده از تابع چگالی احتمالی گوس (Gaussian Probability Density Function: PDF) تعیین می‌گردد. در این تابع متغیرها براساس درجه پراکندگی ذرات در اثر نوسانات آشفته تعریف می‌شوند. مسیر متوسط نیز با حل همزمان معادلات میانگین گیری شده دسته جمعی (Ensemble-Average) برای حرکت تمام ذرات موجود در ابر ذرات بدست می‌آید.

ابر مذکور بصورت یک نقطه چشمه (Point-Source) یا قطر اولیه وارد دامنه محاسباتی می‌شود. این ابر بواسطه پراکندگی آشفته در طی مسیر تا مرز خروجی گسترش می‌یابد. همانطور که قبلا اشاره شد توزیع ذرات در ابر با استفاده از PDF و براساس موقعیت ابر نسبت به مرکز آن مشخص می‌شود. مقدار PDF بیانگر احتمال رویت ذرات موجود در ابر با زمان اقامت t در مکان x_i در میدان جریان است. چگالی میانگین ذرات می‌تواند از طریق وزن دهی نرخ کلی جریان ذرات واقع در ابر، mdot، و بصورت معادله (35) تعریف می‌شود.

تئوری حرکت ذره :

PDFهای موقعیت ذره بصورت یک تابع گوسی چند متغیره فرض می‌شوند (رابطه 36) این متغیرها شامل میانگین (معادله 38) و واریانس (معادله 39) هستند که در معادلات (36) و (37) حضور دارند. میانگین PDF یا همان مرکز ابر ذره در یک زمان مشخص، مبین محتمل‌ترین موقعیت ذرات در ابر است. موقعیت متوسط با انتگرال گیری سرعت ذرات بصورت تابعی از معادله حرکت ابر ذرات محاسبه می‌شود (معادله 38). این معادله حرکت براساس متوسط جمعی (Ensemble-Average) بنا شده است. شعاع ابر ذرات به واریانس PDF وابسته است. واریانس PDF را می‌توان در ترم‌های مقادیر آماری آشفتگی در ذره و در قالب رابطه (39) بیان نمود.

تابع تصحیح سرعت برای اندازه گیری سرعت پراکندگی ذرات در مدل ابر ذرات بکار گرفته شده است. نرم افزار Fluent از رابطه پیشنهادی مقدماتی ونگ (Wang) و مورد استفاده توسط جین (Jain) استفاده می‌کند. جائیکه بردار جاذبه در جهت محور Z تنظیم شده باشد R_ij از رابطه (43) محاسبه می‌شود.

در رابطه (43) Ʈ_a زمان پاسخ آئرودینامیکی ذره می‌باشد که با استفاده از معادله (46) تعیین می‌گردد.

تئوری حرکت ذره در مدل DPM:

با استفاده از این تابع تصحیح، واریانس روی زمان عمر ابر ذره انتگرال گیری می‌شود. در هر زمان مشخص انحراف معیار، شعاع ابر ذره در سه جهت اصلی محورهای مختصات تنظیم می‌شود. شعاع ابر ذره به انحراف معیار حداقلی 99.2% از مساحت محاسبه شده توسط PDF در این فاصله محدود می‌شود. پس از تعیین سلول‌های واقع در داخل ابر ذرات، مشخصات سیال برای مسیر میانگین، متوسط‌گیری حجمی شده و مسیر میانگین روی زمان انتگرال گیری می‌شود. این مهم با استفاده از فاکتور وزنی تعریف شده در رابطه (57) صورت می‌گیرد. درصورت محاسبات کوپله، چشمه‌ها براساس همین فاکتور وزنی در داخل سلول‌ها توزیع می‌شوند.

حداقل و حداکثر قطر ابر ذرات تنها ورودی‌های مورد نیاز برای این مدل هستند. مدل ابر ذرات برای هر تزریق فعال و قابل استفاده است. قابل توجه است که این مدل برای رهگیری ناپایای (گذرای) ذرات قابل استفاده نیست.

تئوری حرکت ذره در مدل DPM:

انتگرال گیری معادله حرکت ذره (Integration of Particle Motion Equation)

معادلات مسیر و هرگونه معادلات کمکی توصیف کننده انتقال گرما یا جرم به/از ذرات با انتگرال گیری قدم به قدم گام زمانی گسسته حل می‌شوند. انتگرال گیری زمانی از معادله (1) سرعت ذره در هر نقطه از مسیر را نتیجه می‌دهد. مسیر نیز با استفاده از رابطه (58) پیش بینی می‌شود. قابل توجه است که معادله (1) و (58) از دسته معادلات دیفرانسیلی معمولی (ODE) هستند. معادله (1) فرم عمومی معادله (59) نیز قابل نوشتن است. در این معادله a شتاب ناشی از تمامی نیروها بجز درگ می‌باشد. این دسته معادلات را می‌توان با انتگرال گیری تحلیلی برای مقادیر a، u و Ʈ_p حل نمود.

برای سرعت ذره در مکان جدید uⁿ⁺¹_p از رابطه (60) استفاده می‌شود. موقعیت جدید ذره، xⁿ⁺¹_p ، نیز مشابه با رابطه (60) و طبق معادله (61) بدست می‌آید. در این معادلات uⁿ_p و uⁿ بیانگر سرعت ذره و سیال در موقعیت قبلی هستند. معادلات (60) و (61) در صورت انتخاب روش گسسته سازی تحلیلی قابل استفاده خواهند بود.

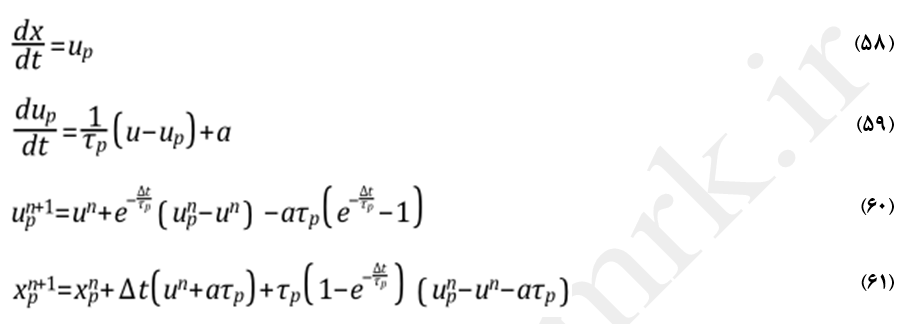
دسته معادلات (1) و (58) با استفاده از روش‌های عددی هم می‌توانند حل شوند. درصورت بکارگیری گسسته سازی ضمنی اویلر در معادله (59) به معادله (62) می‌رسیم. اگر از گسسته‌سازی (انتگرال گیری) ذوزنقه‌ای استفاده شود، لازمست مقادیر u_p و u_n برای سمت راست معادله لحاظ گردد. جائیکه شتاب‌های a ناشی از سایر نیروها ثابت فرض می‌شود (معادله 63). مقدار میانگین متغیرهای u^*_p و u^* با استفاده از روابط (64-66) بدست می‌آیند. سرعت ذره در مکان جدید (n+1) نیز طبق رابطه (67) محاسبه می‌شود.

برای روش‌های ذوزنقه‌ای و ضمنی، مکان جدید ذرات همواره با انتگرال گیری از طریق گسسته سازی ذوزنقه‌ای معادله (58) تعیین می‌گردد (رابطه 68). معادلات (58) و (59) با استفاده از روش رانگ-کوتای پیشنهادی توسط کش (Cash) و کارپ (Karp) حل می‌شوند. معادلات دیفرانسیل معمولی را می‌توان بصورت یک بردار در نظر گرفت که سمت چپ معادله مشتق بردار y و سمت راست آن یک تابع دلخواه است (معادلات 69-71).

تئوری حرکت ذره در مدل DPM:

این روش موجب ایجاد کنترل روی خطای جاداده‌شده (Embedded Error) گشته و درصورتیکه Accuracy Control فعال باشد، از دسترس خارج است.

برای جریان در قاب‌های مرجع متحرک (MRF)، این انتگرال گیری روی قاب متحرک همراه با ترم‌های اضافی تشریح شده در معادلات (9) و (10) صورت می‌گیرد. بنابراین در حل میدان جریان دورانی هم قابل استفاده است. با استفاده از راه‌کارهای موجود برای کنترل دقت، انتگرال گیری مسیر در زمان با دقت مناسبی انجام خواهد شد.

اندازه گام انتگرال گیری در روش‌های مرتبه بالاتر، نظیر ذوزنقه‌ای و رانگ کوتا، به بازه پایدار مبتنی بر زمان پاسخ ممنتم ذره محدود می‌باشد. بنابراین پیشنهاد می‌شود که از آن‌ها همراه با انتخاب روش ردیابی خودکار استفاده شود.

بدیهی است که روش تحلیلی بسیار مؤثر است. این روش می‌تواند برای گام‌های بزرگ و در وضعیت‌هایی که در آن ذره از تعادل هیدوردینامیکی با جریان پیوسته برخوردار نیست، غیر دقیق باشد. روش‌های عددی ضمنی و ذوزنقه‌ای همراه با انتخاب روش ردیابی خودکار، Automated Tracking Scheme Selection: ATSS، اغلب تغییرات روی نیرو‌های عمل کننده بر ذرات را در نظر می‌گیرد. روش رانگ-کوتا نیز برای تغییرات بدون نیروی درگ در راستای گام انتگرال گیری ذره پیشنهاد می‌گردد.

برای ذرات بدون جرم، سرعت ذره با سرعت جریان اصلی برابر است. بنابراین تنها حل معادله مسیر (58) مورد نیاز است چراکه u_p= u می‌باشد. مکان جدید ذره در امتداد مسیر همیشه با استفاده از معادلات (64) و (68) و با فرض u_p= u حل می‌شود. همچنین معادله حرکت ذره دوار (معادله 217) با انتگرال گیری ضمنی اویلر حل می‌شود.

بازگشت

مطالب مرتبط

Researchers develop new theory to explain random movement of particles in fluids