تئوری مدل شکست موجی
Wave Breakup Model Theory
تئوری مدل شکست موجی ریتز (Reitz) در مرجع [1] یک جایگزین مناسب برای مدل شکست تشابهی تیلور TAB در عددهای وبر بالا به شمار میرود. در این مدل شکست قطرات به واسطه سرعت نسبی بین فازهای گاز و مایع اتفاق میافتد. مدل مذکور فرض میکند که زمان شکست و همچنین اندازه قطرات حاصله با ماکزیمم رشد ناپایداری کلیون-هلمهولتز (Kelvin-Helmholtz Instability) برگرفته از تحلیل ناپایداری جت توصیف شده در ادامه، وابسته است.
کاربردها و محدودیتها
تئوری مدل شکست موجی برای انژکتورهای سرعت بالا مناسب است. جائیکه اعتقاد بر اینست که ناپایداری کلوین-هلمهولتز بر شکست قطرات قالب است. از آن جائیکه مدل شکست موجی میتواند تعداد پارسلهای (Parcels) محاسباتی را افزایش دهد لذا ممکن است بخواهید در ابتدا تعداد کمی از قطرات را تزریق کنید.
تحلیل پایداری جت(Jet Stability Analysis)
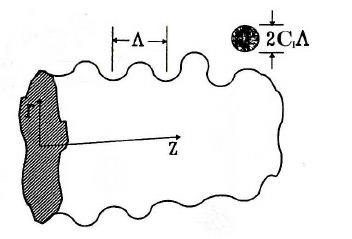
تحلیل پایداری جت برگرفته از تحقیقات ریتز و براکو (Bracco) در مرجع [2] در اینجا تشریح شده است. این تحلیل پایداری یک جت لزج استوانهای با شعاع a و سرعت v از یک اوریفیس دایروی که وارد یک گاز غیر لزج، تراکم ناپذیر، و ساکن با چگالی ρ2 میشود را بررسی میکند. ρ1 و μ1 به ترتیب چگالی و لزجت مایع است. در این تحلیل از سیستم مختصات قطبی استوانهای که همراه با جت حرکت میکند استفاده میشود.
یک جابجایی مسطح متقارن محوری بینهایت کوچک و البته دلخواه (معادله 403) بر بروی حرکت پایدار اولیه چت تحمیل میشود. در نتیجه یافتن یک رابطه پراکندگی مناسب، ω=ω(k)، که بخش حقیقی نرخ رشد، ω، را به عدد موج K=2π/λ مرتبط کند، مطلوب است. برای تعیین مقدار رابطه پراکندگی، روابط خطی شده هیدرودینامیکی با فرض روابط حاکم (404) و (405) حل میشوند.

در روابط فوق φ1 و ψ1 به ترتیب پتانسیلهای سرعت و تابع جریان،
C1 و C2 ثابتهای انتگرال،
I0 و I1 توابع بسل نوع اول و
L2=K2+ω/ν1 و ν1 لزجت سینماتیکی میباشد [1].
فشار مایع از بخش غیر لزج معادلات مایع بدست میآید. بعلاوه، معادلات گاز غیر لزج را میتوان برای محاسبه نوسانات فشار گاز در r=a حل نمود (معادله 406). در معادله (406) K0 و K1 توابع بسل بهینه شده نوع دوم و u سرعت نسبی بین مایع و گاز هستند. شرایط مرزی خطی شده هم طبق معادلات (407) تا (409) تعریف میشوند. این روابط شرط سطح آزاد جنبشی مایع، پیوستگی تنشی برشی و پیوستگی تنشهای عمودی را به صورت ریاضی تفسیر میکنند. توجه داشته باشید که u1 اغتشاشات محوری سرعت مایع، v1 اغتشاشات شعاعی سرعت مایع و σ تنش سطحی میباشند. همچنین دقت کنید که معادله (408) تنها با فرض v2=0 حل میشود.
همانطور که توسط ریتز بیان شد، معادلات (407) و (408) را میتوان برای حذف ثابتهای انتگرال C1 و C2 در معادلات (404) و (405) به کار برد. بنابراین موقعی که حلهای فشار و سرعت در معادله (409) جایگزین میشوند، رابطه (410) حاصل میشود. ریتز نشان داد که معادله (410) پیش بینی میکند که برای هر ویژگی جریان، بیشترین نرخ رشد (یا همان ناپایدارترین موج) هم وجود دارد. برآزشهای منحنی معادله (410) که با استفاده از آنها بیشترین مقدار رشد، Ω، و طول موج متناظر با آن، Λ، به دست میآیند، طبق روابط (411) و (412) تعریف میشوند.

در روابط فوق Oh: عدد اونسرج (Ohnesorge number)،
Ta: عدد تیلور
We1: عدد وبر مایع
We2: عدد وبر گاز و
Re1: عدد رینولدز هستند.
شکست قطره
در مدل موج شکست پارسلهای قطره با فرض اینکه شعاع قطرات تازه تشکیل شده با طول موج سریعترین رشد موج سطحی ناپایدار روی قطره والد (Parent Droplet) متناسب است محاسبه میشود (معادله 413). در رابطه (413) B0 ثابت مدل و برابر با 0.61 است [1]. علاوه بر این نرخ تغییرات شعاع قطره در پارسلهای والد از معادله (414) به دست میآید.

در روابط فوق، τ زمان شکست است. Λ و Ω هم با استفاده از معادلات (411) و (412) محاسبه میشوند. طبق پیشنهاد لیو (Liu) و همکاران [3] ثابت زمان شکست، B1، برابر با 1.73 تنظیم میشود. مقادیر B1 میتواند بین 1 تا 60 و بسته به مشخصات انژکتور تغییر کند.
در مدل موج مقدار جرم از قطره والد در نرخ تعیین شده توسط معادله (415) جمع میشود تا اینکه جرم تراوش (Shed) برابر با 5% جرم پارسل اولیه شود. در این زمان یک پارسل جدید با شعاع بدست آمده از معادله (413) ایجاد میشود. به پارسلهای جدید همان ویژگیهای پارسل اصلی (دماف جنس ماده، مکان و غیره) به استثنای شعاع و سرعت، اعطا میشود! در واقع به پارسل جدید سرعتی داده میشود که به طور تصادفی در صفحه عمود بر بردار جهت پارسل اولیه (والد) واقع شده است. البته ممنتم پارسل والد نیز به گونهای تنظیم میشود که قانون بقای ممنتم حاکم باشد. قابل توجه است که اندازه سرعت پارسل جدید با پارسل اولیه برابر است.
لازمست ثابتهای مدل را به اندازهای مشخص کنید تا تعیین کند که فاز گاز چگونه با قطرات مایع اندرکنش خواهد داشت. به عنوان مثال ثابت زمان شکست، B1، ثابتی است که با مقیاس زمانی که مشخص میکند پارسل با چه سرعتی کاهش وزن میدهد، ضرب میشود. بنابراین مقدار بزرگتر این ثابت به این معنی است که پارسل مقدار معینی از جرم خود را در زمان بیشتری از دست میدهد. مقدار بیشتر B1 در بحث اندرکنش با فاز گاز به این معنی است که اندرکنش با زیر شبکه شدت کمتری دارد. B0 ثابت مرتبط با اندازه قطره است و معمولا برابر با 0.61 در نظر گرفته میشود.
در شکست اولیه جت مایع استوانهای در عدد وبر پایین (رژیم ریلی)، معادله (413) میتواند قطر قطره را بیشتر از قطر (جت) اولیه پیش بینی کند. در این حالت، اندازه قطره از سریعترین طول موج رشد (که فاصله قطرات اولیه را مشخص میکند) و همچنین با توجه به ملاحظات قانون بقای جرم، محاسبه میشود. شما میتوانید از این محاسبات در رژیم ریلی صرف نظر کرده و آن را انجام ندهید.
:[1]
R. D. Reitz. “Mechanisms of Atomization Processes in High-Pressure Vaporizing Sprays”. Atomization and Spray Technology. 3. 309–337. 1987.
:[2]
R. D. Reitz and F. V. Bracco. “Mechanisms of Breakup of Round Liquid Jets”. The Encyclopedia of Fluid Mechanics, ed. N. Cheremisnoff.3. 223–249. 1986.
:[3]
A. B. Liu, D. Mather, and R. D. Reitz. “Modeling the Effects of Drop Drag and Breakup on Fuel Sprays”. SAE Technical Paper 930072.SAE. 1993.
:[4]
https://www.researchgate.net/figure/The-Wave-model-relates-breakup-to-Kelvin-Helmholtz-instability-and-product droplet-size_fig3_234154283