تئوری مدل شکست اشمل

تئوری مدل شکست اشمل

Schmehl Breakup Model Theory

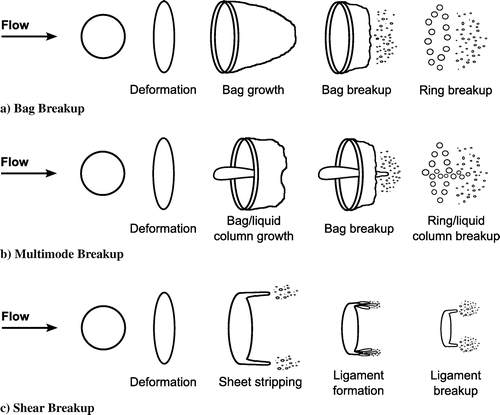
تئوری مدل شکست اشمل [1] بین سه رژیم شکست زیر تفاوت قائل است:

1. مدل شکست کیسه (Bag Breakup)
2. مدل شکست چند حالته (Multimode Breakup)
3. شکست برشی (Shear Breakup)

این رژیم‌ها (شکل-1) به وسیله عدد وبر که قدرت نیروهای آئرودینامیکی را نسبت به نیروهای تنش سطح اندازه می‌گیرد (معادله 442) و عدد اونسرج (Ohnesorge Number) تعریف شده توسط رابطه (443) که اثر میرایی اصطکاک چسبندگی در قطره را در برابر کشش سطحی ارزیابی می‌کند از یکدیگر تشخیص داده می‌شوند.

شکل-1: مکانیزم‌های شکست قطرات آب در اعداد وبر مختلف [1].

در روابط فوق:

ρ_g: چگالی گاز،

U_rel: سرعت نسبی گاز-قطره،

D_parent: قطر قطره قبل از شکست (قطره والد)

ρ_l: چگالی قطره و

σ_l: تنش سطحی قطره مایع هستند.

انتقال بین مکانیزم‌های مختلف شکست توسط توابع وابسته به عدد وبر محلی زیر مدل‌سازی می‌شود.

سه مکانیزم شکست بالا از سرعت‌های نرمال، نقطه-زمان شکست و توزیع حجمی متفاوت برای بچه قطره‌ها استفاده می‌کنند. در تمام رژیم‌ها، فرآیند شکست به دو مرحله زیر تقسیم می‌شود:

• تغییر شکل اولیه قطره به دیسک
• تداوم تغییر شکل دیسک با فروپاشی قطرات

مدل شکست اشمل از مکانیزم تغییر شکل و تجزیه پیشنهادی توسط پیلچ (Pilch) و اردمن (Erdman) استفاده می‌کند [3]. پریود زمانی، تغییر شکل، ضریب درگ، مساحت مرجع برای محاسبه درگ و نیروی درگ قطره با استفاده از معادلات (426) تا (432) محاسبه می‌شود.

زمان کل شکست، t_b، به عدد وبر محلی وابسته است. به طوریکه برای اعداد انسرج کوچکتر از 1، Oh<1، از معادله (433) و برای اعداد اونسرج بزرگتر از یک، Oh>1، از رابطه (444) برای محاسبه t_b استفاده می‌شود. قابل توجه است که در اعداد انسرج بزرگتر از یک، لزجت مایع بر فرآیند فروپاشی قطرات غالب است. سرعت بچه قطره ناشی از انبساط گوشه اوریفیس از طریق معادله (434) محاسبه می‌شود. اندازه سرعت نرمال u_n در صفحه عمود بر بردار سرعت والد، U_parent، به رژیم شکست بستگی دارد.

همانند مدل ماداووشی برای هریک از بچه قطره‌ها زاویه جهت سرعت عمودی، α، به طور تصادفی در محدوده صفر تا 2π انتخاب می‌شود. تعداد بچه قطره‌ها برخلاف مدل ماداووشی روی مقدار 5 ثابت در نظر گرفته نمی‌شود. طبق پیش فرض این مقدار 1 است اما می‌توان آن را در کد نویسی و یا استفاده از  نرم افزار Fluent تغییر داد.

در رژیم‌های شکست کیسه و چندحالته توزیع حجمی هدف بچه قطرات پس از شکست توزیع نرمال ریشه (معادله 436) توصیف شده در مدل شکست ماداووشی بدست می‌آید. در رژیم شکست کیسه، جرم کلی پارسل قطره والد (Mparent) به طور یکنواخت بین پارسل‌های بچه قطره‌ها توزیع می‌شود. برای رژیم شکست برشی، 20% جرم کل پارسل قطره‌های والد به عنوان جرم باقیمانده قطره والد حفظ شده و 80% دیگر به طور یکنواخت بین پارسل‌های بچه قطره‌ها تقسیم می‌شود. اما رژیم چند حالته، وضعیتی بین دو رژیم کیسه و برشی است. این رژیم جرم تراوش یافته را با استفاده از میانگین‌گیری خطی بین دو رژیم دیگر و براساس عدد وبر معرف آن‌ها محاسبه می‌کند.

در رژیم چند حالته (We_mu<We<=We_shear)، جرم باقیمانده در پارسل قطره والد، M_core، از معادله (448) بدست می‌آید. همچنین توزیع یکنواخت هر بچه قطره از رابطه (449) محاسبه می‌شود. سرانجام مشخصات بسته قطرات والد باقیمانده بر اساس قطر جدید پیروی کننده از توزیع حجمی هدف بچه قطره‌ها بعد از شکست، و همچنین نرخ جدید جریان و تعداد پارسل‌ها که بر اساس رابطه مبتنی بر M_core به دست می‌آید، تصحیح می‌شود.

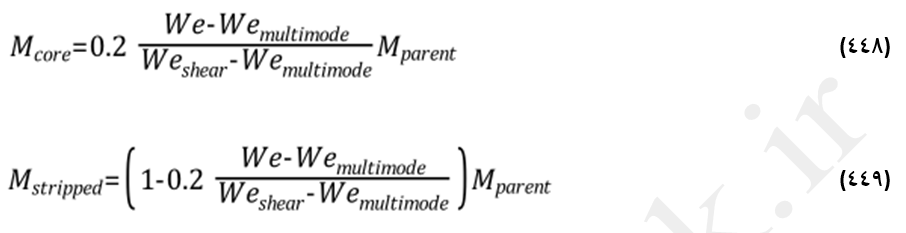
در رژیم شکست برشی، توزیع حجمی بچه قطره‌ها توسط یک تابع چگالی دو-مودی (Bimodal) با حداکثر مقدار اول در ناحیه قطر‌های قطرات کوچک و حداکثر مقدار دوم در قطرهای قطرات بزرگ مشخص می‌شود. کسر جرمی تراوشات قطرات بیانگر تقریبا  80% از جرم بسته قطرات والد است. این قطرات از تراوشات فیلم مایعی است که توسط نیروهای برشی از قطره دیسکی شکل جدا می‌شود. 20% باقی‌مانده در ناحیه قطر بزرگ بیانگر سهم تراوشات قطرات هسته تشکیل شده توسط فرآیند سلب است. قطر این قطره هسته، D_crit، از عدد وبر بحرانی، We_crit، در شرایط جریان در لحظه شکست، تخمین زده می‌شود (معادله 450).

توزیع حجمی بچه قطره‌های جدا شده با همان توزیع نرمال ریشه در مدل شکست ماداووشی (معادله 436) به دست می‌آیند. به هر صورت پارسل‌ها همانند رژیم‌های شکست کیسه و چند حالته از روابط (451) و (453) محاسبه می‌شود. قطر قطرات پارسل والد نیز طبق معادله (454) تصحیح می‌شود.

نرخ جریان جدید و تعداد در پارسل قطرات والد پس از شکست بر اساس M_core=0.2M_parent محاسبه می‌شوند. از آنجائیکه ممکن است D_crit گاهی و بسته به عدد وبر بحرانی، We_Crit، از قطر قطره والد بزرگتر شود، لذا بیشترین مقدار قطر پارسل قطرات باقیمانده به قطر قطرات قبل از شکست محدود می‌شود. اگر تعدا پارسل 1 فرض شود، شکست آماری کامل می‌شود و هیچ پارسل بچه قطره‌ای تراووش نمی‌کند. پارسل قطرات والد با قطر جدید، دبی جریان جدید و تعداد جدید قطرات در پارسل طبق روابط (455) تا (458) به روز رسانی می‌شود.

 

 

 

 

 

 

:[1]

R. Schmehl, G. Klose, G. Maier, S. Wittig. “Efficient Numerical Calculation of Evaporating Sprays in Combustion Chamber Flows”. In RTO AVTSymposium on Gas Turbine Engine Combustion Emissions and Alternative Fuels, Lisbon, Portugal, 1998. RTO MP-14. 51.1–51.14.1999.

 

:[2]

https://arc.aiaa.org/doi/10.2514/1.B35819

:[3]

M. Pilch and C. A. Erdman. “Use of Breakup Time Data and Velocity History Data to Predict the Maximum Size of Stable Fragments for Acceleration-Induced Breakup of a Liquid Drop”. Int. J. Multiphase Flow. 13. 6. 741–757. 1987.