حل معادلات هذلولوی به روش تفاضل محدود

Solving Hyperbolic PDEs Using FDM

حل معادلات هذلولوی به روش تفاضل محدود در این پست توضیح داده شده است. معادله موج معروف‌ترین معادله در معادلات مشتقات جزئی به شمار می‌رود. به همین خاطر حل این معادله با استفاده از روش‌های متنوع تفاضل محدود مورد بررسی قرار گرفته شده است. معادله (1) یک معادله موج کلاسیک است. معادله (2) نیز یک معادله موج مرتبه اول می‌باشد.

روش‌های گوناگونی برای حل عددی معادله موج مطرح شده که در قالب دو نوع صریح و ضمنی می‌باشد. این روش‌ها [1] در معادله موج مرتبه اول (معادله 1) در قالب مثال (1) و در معادله موج کلاسیک بصورت مثال (2) بطور کامل تشریح شده است.

حل عددی معادلات هذلولوی مرتبه اول با روش‌های تفاضل محدود

بعنوان اولین مثال، معادله موج مرتبه اول زیر را در نظر بگیرید (مثال-1). در این معادله سرعت صوت (300 متر بر ثانیه) می‌باشد. فرض کنید که اغتشاشی در داخل یک لوله یک بعدی که هر دو انتهای آن بسته می‌باشد، اعمال شده است. این اغتشاش در زمان t=0 به شکل یک موج سینوسی با شرائط اولیه زیر اعمال شده است:

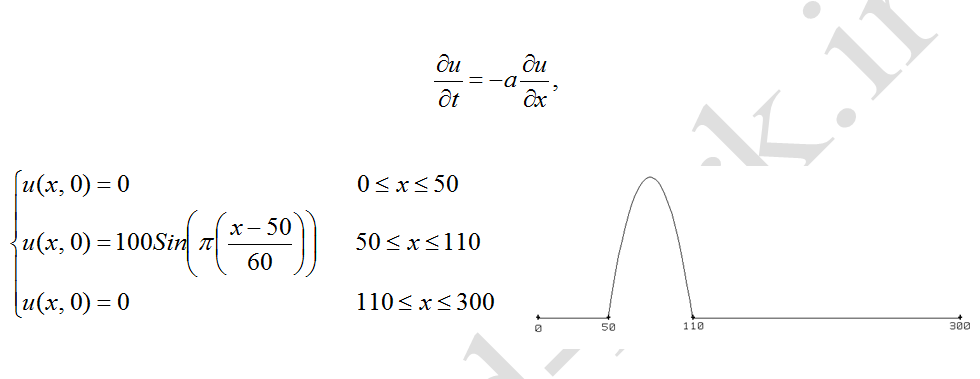
هدف حل عددی معادله فوق با استفاده از روشهای مختلف عددی و مقایسه آن با حل تحلیلی (دقیق) می‌باشد.

روش‌های صریح حل عددی معادله موج مرتبه اول

الگوریتم‌های متعددی برای گسسته‌سازی صریح معادله موج مرتبه اول (معادله 2) پیشنهاد شده که در این قسمت به مهمترین آنها اشاره شده است. الزاماً تمامی روشهای بیان شده پایدار نیست و بهمین خاطر پایداری این روش‌ها نیز مورد بررسی قرار گرفته و توضیح داده شده است.

روش تفاضل پیش رو در زمان و پسرو در مکان (Forward in Time and Backward in Space: FTBS)

در روش تفاضل بالادست معادله (2) بصورت پیش رو در زمان و پسرو در مکان گسسته سازی می‌شود. این فرم گسسته شده در معادله (3) نشان داده شده است. با توجه به این معادله می‌توان دریافت که دقت این روش از مرتبه یک (Δx) است. از آنجا که روش یاد شده یک روش صریح است، بنابراین لازم است که پایداری این روش بررسی شود. در این جا پایداری این روش با استفاده از آنالیز پایداری ون-نیومن مورد بررسی قرار می‌گیرد. با استفاده از بسط سری تیلور u_iⁿ بصورت معادله (4) بازنویسی می‌شود:

در معادله (4) G ضریب رشد یا همان بزرگی دامنه و p عدد موج در جهت x می‌باشد. با توجه به رابطه فوق، معادله (3) را می‌توان در قالب بسط سری فوریه در معادله (5) بازنویسی کرد. با فاکتور گیری از این معادله رابطه (6) حاصل می‌شود. شرط لازم و کافی برای صادق بودن معادله (6)، این است که رابطه (7) برقرار باشد. از آنجا که دامنه p بین مثبت و منفی بی‌نهایت است و همچنین با تعریف –pΔx=θ و با توجه به روابط جبر مختلط معادله (8) بدست می‌آید.

در نتیجه، به ازای مقادیر C≤1، این روش یک روش پایدار است. محدوده پایداری C در شکل (1) نشان داده شده است. قابل توجه است که اگر اندازه شعاع دایره کوچک‌تر، G، کمتر از واحد باشد، روش صریح تفاضل FTBS پایدار خواهد بود. پارامتر C را اصطلاحاً عدد کورانت(Courant Number) یا عدد CFL: Courant-Fredrich-Levy نیز می‌نامند.

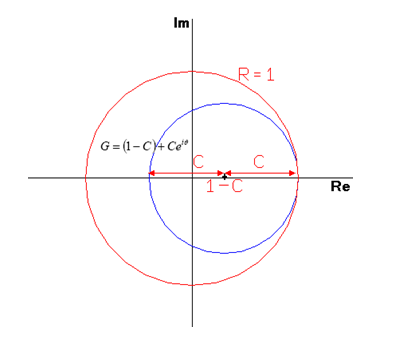
شکل-1: محدوده پایداری در فضای مختلط.

مثال-1 که در قسمت قبل توضیح داده شده، در این قسمت با استفاده از روش FTBS صریح بصورت عددی حل شده است. شکلهای (2) و (3) بیانگر نتایج بدست آمده از این روش می‌باشد. در شکل (2) چگونگی حرکت موج در صفحه (x,t) نشان داده شده است. در شکل (2-الف) با افزایش زمان طول موج (اندازه موج در جهت x) افزایش و دامنه آن (اندازه موج در جهت z) کاهش می‌یابد. در حالیکه در شکل (2-ب) هم طول موج و هم دامنه آن ثابت باقی می‌ماند. علت این امر، انتخاب مقدار C است. هرچه مقدار C به مقدار یک نزدیکتر باشد، حل عددی حاصل از روش صریح FTBS دقیقتر بوده و به حل تحلیلی نزدیکتر است.

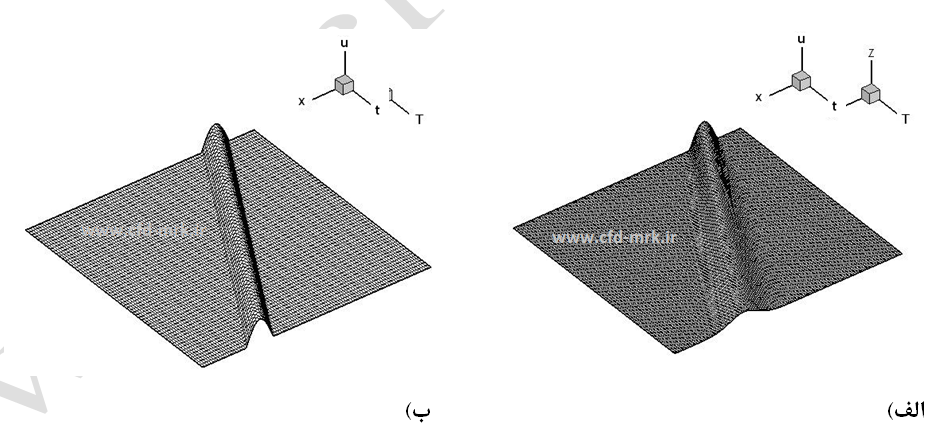
شکل-2: حل عددی معادله موج مرتبه یک با استفاده از روش FTBS صریح. الف: C=0.45، ب: C=0.9996.

در شکل (3) موقعیت و اندازه موج در زمان 45/0 ثانیه نشان داده شده است. همانطور که در این شکل نیز مشخص است، در زمان 0.45 ثانیه حل حاصل از C=0.45 دارای طول موج بزرگتر و دامنه کوچکتر نسبت به حل حاصل از C=0.9996 و حل تحلیلی می‌باشد. نتایج بدست آمده براساس C=0.9996 نیز در این شکل ارائه شده و نشان می‌دهد که با افزایش مقدار C تا یک، جوابها دقیقتر می‌شود.

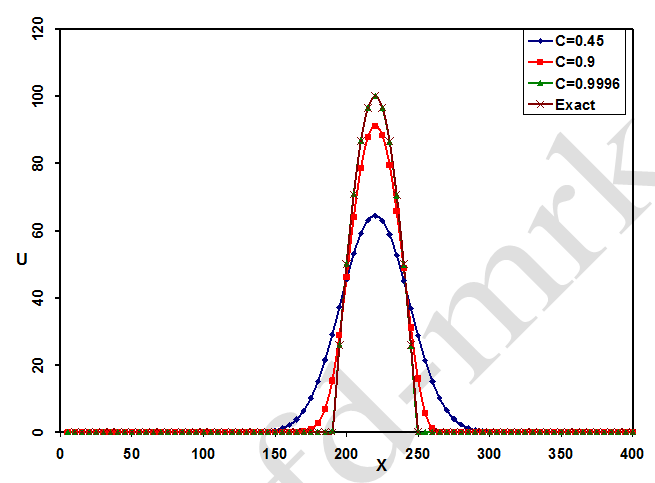
شکل-3: مقایسه بین نتایج بدست آمده از روش FTBS صریح با استفاده از اعداد کورانت مختلف در زمان t=0.45 S.

از آنجا که روش FTBS صریح یک روش تفاضل مرتبه اول است بنابراین خطای موجود از نوع خطای اضمحلالی می‌باشد. لذا انتظار بر اینست که خطای حاصل از این روش بصورت تغییر در اندازه دامنه ظاهر شود. این پدیده را بوضوح می‌توان در شکلهای (2) و (3) مشاهده نمود.

روش صریح پیشرو در زمان و پیشرو در مکان (FTFS: Forward in Time and Forward in Space )

روش FTFS صریح اویلر براساس تقریب تفاضل پیشرو مرتبه اول برای هر دو ترم زمانی و مکانی استفاده تعریف می‌شود. فرمولاسیون کلی این روش برای معادله حاکم در مثال (1) بصورت معادله (9) می‌باشد. در معادله فوق، ترم اول سمت چپ معادله مشکلی ندارد، چراکه از زمانهای قبلی استفاده شده است. اما ترم دوم می‌تواند مشکل ساز باشد. علت این امر اینست که از محاسبات براساس مکانی انجام می‌شود (uⁿ_i+1) که شناخت دقیقی از آن وجود ندارد (هذلولوی بودن). بهمین خاطر لازمست که پایداری آن مورد بررسی قرار گیرد. با استفاده از بسط سری فوریه می‌توان معادله (9) را بصورت معادله (10) بازنویسی کرد. در نتیجه، برای ارزیابی شرط پایداری معادله (11) حاکم است.

تحلیل اول ون-نیومن نشان می‌دهد که این روش بی قید و شرط ناپایدار است. بنابراین استفاده از این روش برای معادله موج مرتبه امکان‌پذیر نیست. البته، وقتی صحبت از ناپایداری به میان می‌آید، منظور اینست که سری فوریه حاصله یک سری واگرا بوده و مقدار پاسخها در هر گام زمانی بشدت افزایش می‌یابد. برای درک بهتر، حل عددی انجام شده بر روی معادله موج مرتبه اول با استفاده از این روش تنها برای زمان بسیار کوچک (کمتر از 0.5 ثانیه) در شکل (4) نشان داده شده است. در این شکل نوسانات بسیار شدید در اندازه دامنه بیانگر ناپایداری روش حل و نتایج بدست آمده می‌باشد.

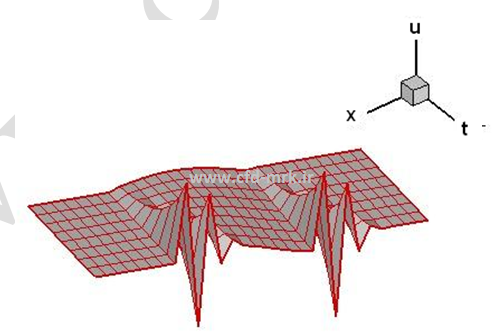
شکل-4: نتایج بدست آمده از روش اف-تی-اف-اس که نشانگر ناپایدار بودن آن می‌باشد.

نتیجه اینکه این روش برای معادله موج مرتبه اول ناپایدار است.

روش صریح اویلر پیشرو در زمان و مرکزی در مکان (Forward in Time and Centered in Space (FTCS) )

روش FTCS صریح اویلر از یک تفاضل پیشرو برای زمان و تفاضل مرکزی برای مکان استفاده می‌کند. گسسته سازی معادله مثال (1) با استفاده از این روش بصورت معادله (12) می‌باشد. این روش نیز ناپایداری دارد. لازم به توضیح است بطور کلی روش پیشنهادی باید از فیزیک مسئله پیروی کرده و با آن مطابقت داشته باشد. اگر این موضوع در هر مسئله‌ای صادق نباشد، پایداری آن روش مسئله ساز خواهد بود. بهمین خاطر پایداری این روش نیز مورد بررسی قرار گرفته است. بسط سری فوریه متناظر با معادله (12) به صورت معادله (13) می‌باشد. البته معادله (13) را می‌توان بصورت معادله (14) نیز بازنویسی کرد. با توجه به معادله (14)، G با استفاده از معادله (15) قابل محاسبه خواهد بود.

رابطه فوق نشان می‌دهد که اندازه G همواره بزرگتر یا مساوی صفر می‌باشد. بنابراین، برای معادله موج مرتبه اول، روش یاد شده یک روش بی قید و شرط ناپایدار و غیر قابل استفاده است.

روش لاکس (Lax Scheme)

در صورت استفاده از روش FTCS صریح اویلر برای معادله موج مرتبه اول، اگر از مقدار متوسط استفاده شود، معادله (12) بصورت معادله (16) بازنویسی می‌شود. با استفاده از بسط سری تیلور و برای بررسی آنالیز پایداری رابطه (17) مد نظر می‌باشد. با توجه به معادله (17)، برای برقراری شرط پایداری لازمست اندازه G در معادله (18) کوچکتر یا مساوی یک باشد (رابطه 19). با نگاهی دقیق‌تر به معادله (16) می‌توان مشاهده نمود که برای ترم اول سمت چپ این معادله رابطه (20) برقرار است.

با توجه به روابط نشان داده شده می‌توان دریافت که ترم لزجت مصنوعی در جوهره این روش وجود دارد. مهمترین ویژگی این ترم اینست که به پایداری کمک کرده و خطاها را بطور چشمگیری کاهش داده و از بین می‌برد (چراکه لزجت اثر صاف کردن پیک‌ها یا همان تیزی‌ها را در حل دارد). اما باید توجه داشت که مقدار آن نباید به اندازه‌ای بزرگ باشد که ماهیت جریان را عوض کند. نتایج بدست آمده از حل عددی معادله مثال-1 در شکلهای (5) و (6) نشان داده شده است.

درشکل (5) چگونگی حرکت موج در صفحه (x,t) نشان داده شده است. همانطور که در این شکل مشخص است، به ازای مقدار C=0.9996 حل عددی با جواب دقیق مطابقت داشته و تقریباً با آن برابر است. اما برای C=0.45 با گذشت زمان از دقت جوابها کاسته می‌شود. از آنجا که گسسته سازی در این روش از دقت مرتبه اول می‌باشد، خطاها در اندازه دامنه جواب ظاهر شده است (شکلهای 5-الف و 6). همچنین، علت کاهش بیش از حد دامنه موج و افزایش طول موج آن در شکل (5-الف) نسبت به روش FTBS صریح، (شکل 3) را می‌توان ناشی از وجود ترم لزجت مصنوعی و در نتیجه اضمحلال جوابها و همچنین ناشی از تفاوت تعریف عدد کورانت، C، (البته با تأثیر بسیار کمتر نسبت به ترم لزجت مصنوعی) دانست. این اختلاف در شکل (7) نشان داده شده است.

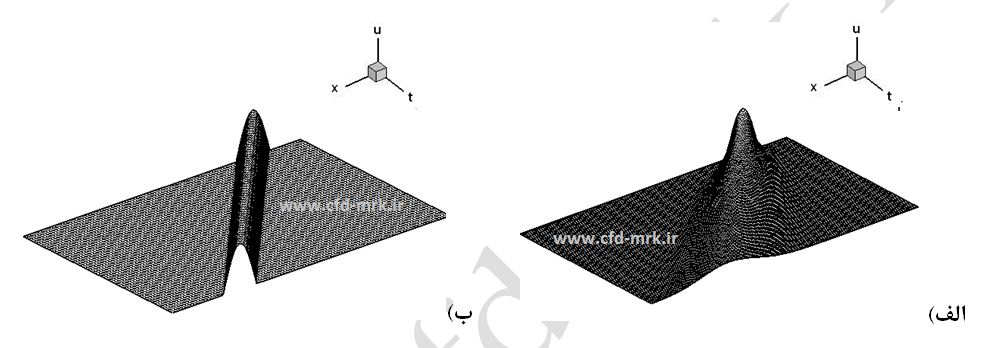
شکل-5: حل معادله موج یک بعدی با استفاده از روش لاکس. الف: C=0.45، ب: C=0.9996.

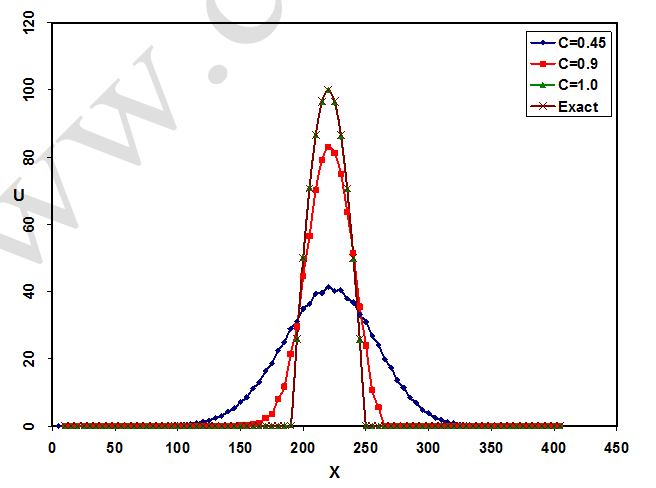
شکل-6: مقایسه بین نتایج بدست آمده از روش لاکس با استفاده از اعداد کورانت مختلف در زمان t=0.45 S.

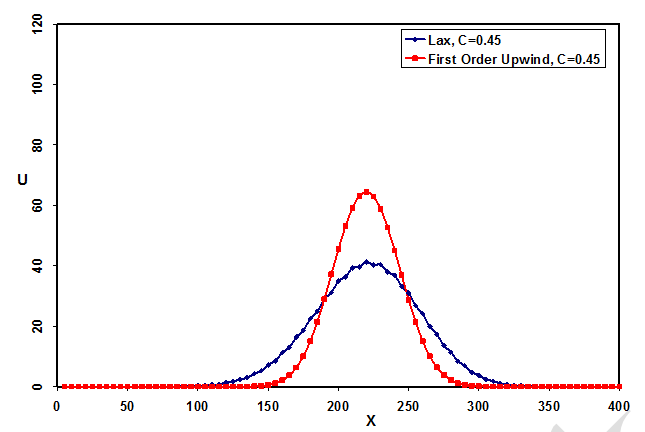
شکل-7: اختلاف بین روشهای FTBS و لاکس با عدد کورانت C=0.45 در زمان t=0.45 S.

روش لاکس-وندروف (Lax-Wendroff Scheme)

روش تفاضل محدود لاکس-وندروف با استفاده از بسط سری تیلور متغیر وابسته بصورت معادلات (21 یا 22) می‌باشد. همچنین با استفاده از معادله موج مرتبه اول و روابط نشان داده شده در معادله (23)، معادله (22) را می‌توان بصورت رابطه (24) بازنویسی کرد. در حقیقت با توجه به روابط 22 و 23، معادله موج مرتبه دوم یا همان معادله موج کلاسیک نتیجه گیری شده است. بنابراین با گسسته‌سازی این معادله به رابطه (24) می‌رسیم که بصورت معادله (25) هم نوشته می‌شود.

روش مذکور از دقت مرتبه دوم زمانی و مکانی بهره می‌برد که در نتیجه دقت مناسبی دارد. نتایج بدست آمده از حل عددی مثال-1 در شکلهای (8) و (9) نشان داده شده است.

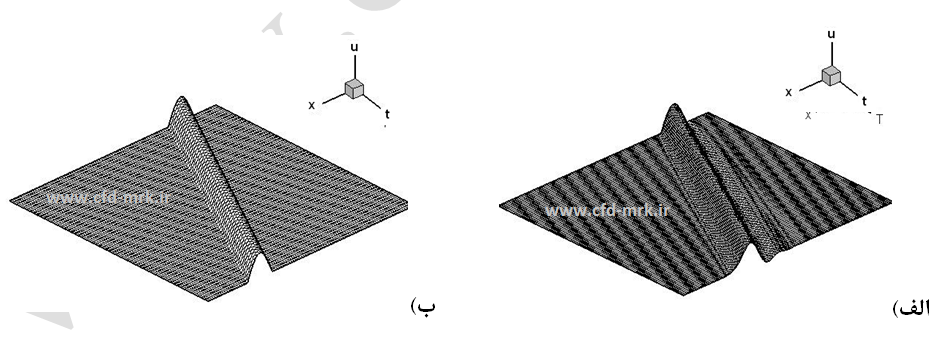
شکل-8: حل معادله موج مرتبه اول با استفاده از روش لاکس-وندروف. الف: C=0.45، ب: C=0.9996.

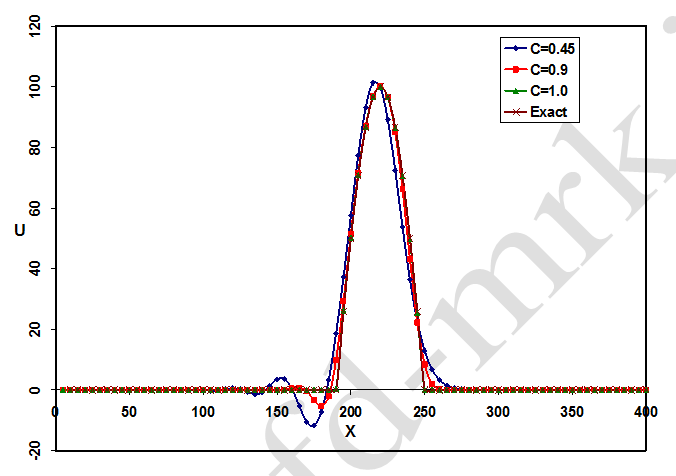
شکل-9: مقایسه بین نتایج بدست آمده از روش لاکس-وندروف با اعداد کورانت مختلف در زمان t=0.45 S.

در شکل‌های (8) و (9) بوضوح مشخص است که چون از جمله فرد (جمله سوم معادلات (22) یا همان معادله (24)) در بسط سری تیلور قطع شده، خطای پدید آمده یک خطای نوسانی است. همچنین، با توجه به شکل‌های مذکور می‌توان دریافت که خطاهای نوسانی روی دامنه حل تأثیر چندانی ندارد و بطور کلی نسبت به خطای دامنه به جواب دقیق نزدیکتر است.

روش مک‌کورمک(MacCormack Scheme)

روش مک‌کورمک روشی است که بطور گسترده برای حل معادلات جریان سیال استفاده می‌شود. در مسائل خطی این روش معادل روش لاکس-وندروف بوده و نتایج بدست آمده از این دو روش مثل هم است. اما، در مسائل غیر خطی روش مک‌کورمک به مراتب از دقت بیشتری برخوردار می‌باشد.

روش مک‌کورمک دارای دو معادله است که هر معادله در یک مرحله مورد استفاده قرار می‌گیرد. این معادلات شامل معادله پیشگو(Predictor) (رابطه 26) و معادله تصحیح کننده(Corrector) (رابطه 27) می‌باشد. علامت (¯) بیانگر مقدار موقتی متغیر وابسته است. اما در معادله دوم یا همان معادله تصحیح کننده از تفاضل پیشرو استفاده می‌شود. در نتیجه، فرم نهایی معادله تصحیح کننده بصورت زیر رابطه (28) بیان می‌شود.

اگرچه فرمولاسیون روش مک‌کورمک کمی پیچیده است، اما هم از نظر مکانی و هم از نظر زمانی از دقت مرتبه دوم برخوردار می‌باشد. همانطور که در معادلات (26) و (28) مشخص است، در مرحله پیشگویی از روش تفاضل پسرو برای u/∂x∂ و در مرحله تصحیح از تفاضل پیشرو برای آن استفاده شده است. این تفاضل‌ها می‌تواند برعکس نیز بکار گرفته شود که در برخی مسائل اینگونه توصیه می‌شود. نتایج بدست آمده از این روش برای مثال-1 در شکل‌های (10) و (11) نشان داده شده است. با مقایسه شکل‌های (10 و 11) با شکل‌های (8 و 9) مشاهده می‌شود که روش مک کورمک برای معادلات خطی همانند روش لاکس-وندروف است.

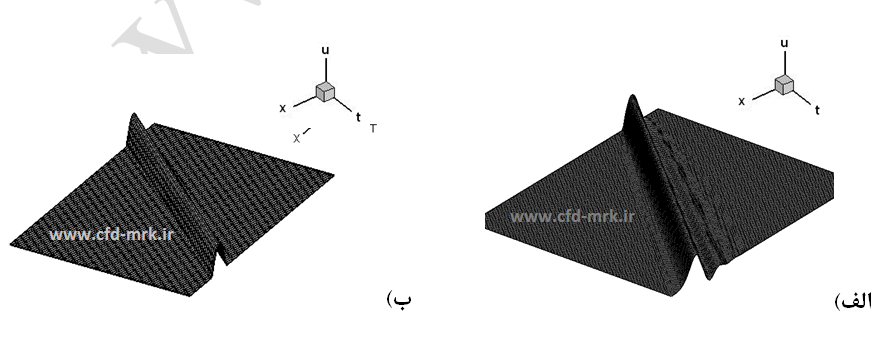
شکل-10: حل معادله موج مرتبه اول با استفاده از روش مک کورمک. الف: C=0.45، ب: C=0.9996.

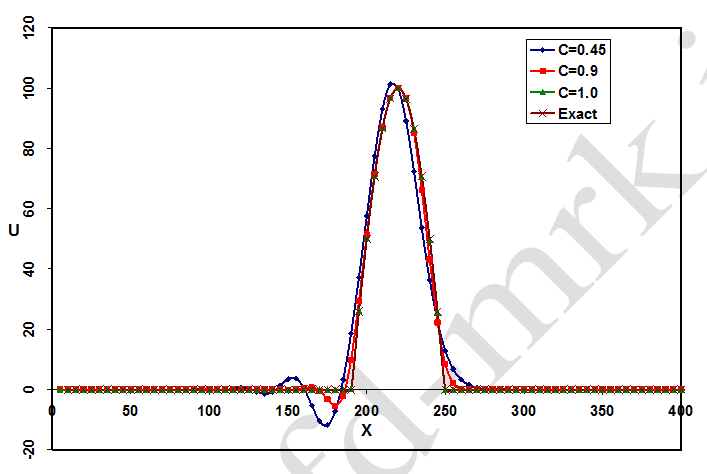
شکل-11: مقایسه بین نتایج بدست آمده از روش مک‌کورمک با اعداد کورانت مختلف در زمان t=0.45 S.

روش‌های ضمنی حل عددی معادله موج

از آنجا که معادله موج خطی است، می‌توان انتظار داشت که در روش‌های ضمنی گسسته‌سازی بی‌قید و شرط پایدار باشد. بنابراین در اینگونه مسائل محدودیت خاصی در انتخاب Δt وجود ندارد. البته باید توجه داشت، با اینکه می‌توان مقدار Δt را به اندازه دلخواه بزرگ انتخاب کرد، اما در صورتیکه مشاهده جزئیات نسبت به گذشت زمان مطلوب باشد، لازمست Δt را به اندازه لازم کوچک انتخاب نمود. در بحث پایداری روشهای ضمنی، هرقدر بتوان گره‌های بیشتری را همزمان درگیر نمود، آنگاه پایداری حل افزایش می‌یابد. روش‌های پسرو در زمان و مرکزی در مکان (BTCS) اویلر و کرانک نیکلسون (Cranck-Nicolson) از مهمترین روش‌های ضمنی گسسته‌سازی معادله موج بشمار می‌رود که در ادامه به آنها اشاره شده است.

روش BTCS اویلر

روش BTCS یک روش تفاضل پسرو در زمان و تفاضل مرکزی در مکان می‌باشد. چگونگی گسسته‌سازی معادله موج با استفاده از این روش بصورت معادله (29) می‌باشد.اگر از معادله فوق در تمام نقاط شبکه استفاده شود، یک دسته معادله جبری خطی حاصل می‌شود که می‌توان آنرا بشکل ماتریسی نیز نشان داد که ماتریس ضرائب آن سه قطری می‌باشد. همچنین، برای آنالیز پایداری این روش می‌توان از همان روش اشاره شده در بخش قبل استفاده می‌شود و بنابراین می‌توان معادله (29) را بصورت رابطه (30) بازنویسی کرد.با توجه به معادله (30)، رابطه (31) حاصل می‌شود. در نتیجه بزرگی G برابر معادله (32) می‌باشد.

بدیهی است که معادله (32) همواره کوچکتر از یک بوده و لذا این روش بی‌قید و شرط پایدار است. نتایج بدست آمده از حل مثال-1 در شکل‌های (12 و 13) نشان داده شده است. با توجه به این شکل‌ها می‌توان دریافت که با افزایش مقدار عدد کورانت مختلف، با گذشت زمان مقدار خطای عددی نیز بیشتر می‌شود.

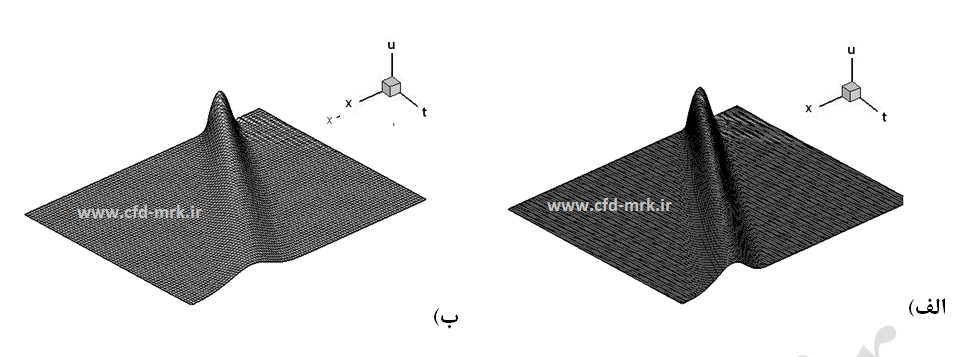
شکل-12: حل معادله موج یک بعدی با استفاده از روش ضمنی بی-تی-سی-اس. الف: C=0.45، ب: C=0.9996.

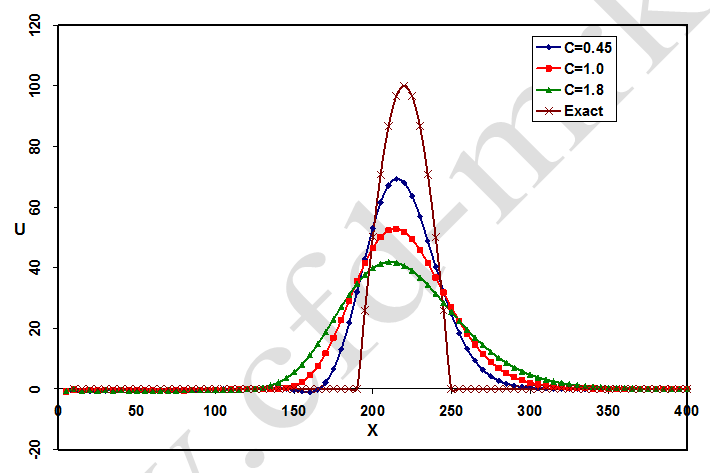
شکل-13: مقایسه بین نتایج بدست آمده از روش ضمنی بی-تی-سی-اس با اعداد کورانت مختلف در زمان t=0.45s.

روش کرنک-نیکلسون (Cranck-Nicolson)

روش کرنک-نیکلسون به نحوی ترکیبی از روشهای صریح و ضمنی می‌باشد. برای درک بیشتر، توجه شود که ترم دوم اولین رابطه معادله (29) را می‌توان بصورت معادله (33) باز نویسی کرد. در معادله (33)، ترم دوم اولین رابطه معادله (29) است بجای اینکه از مرتبه زمانی n+1 باشد، از مرتبه زمانیn+1/2 (میانگین n و n+1) است. فرم نهایی روش کرنک-نیکلسون بصورت معادله (34) است.

این روش از دقت بالا و پایداری بسیار خوبی (بی قید و شرط پایدار) برخوردار بوده و بطور گسترده مورد استفاده قرار می‌گیرد. خطای این روش از نوع نوسانی می‌باشد. همچنین، این روش همانند روش قبل یک دستگاه معادلات سه قطری ایجاد می‌کند. نتایج بدست آمده از حل عددی مثال –1 با استفاده از این روش در شکلهای (14) و (15) نشان داده شده است.

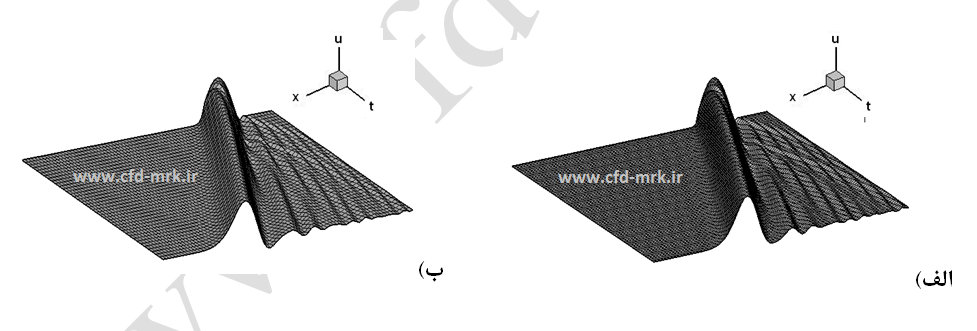
شکل-14: حل معادله موج یک بعدی با استفاده از روش ضمنی کرنک-نیکلسون، الف: C=0.45، ب: C=0.9996.

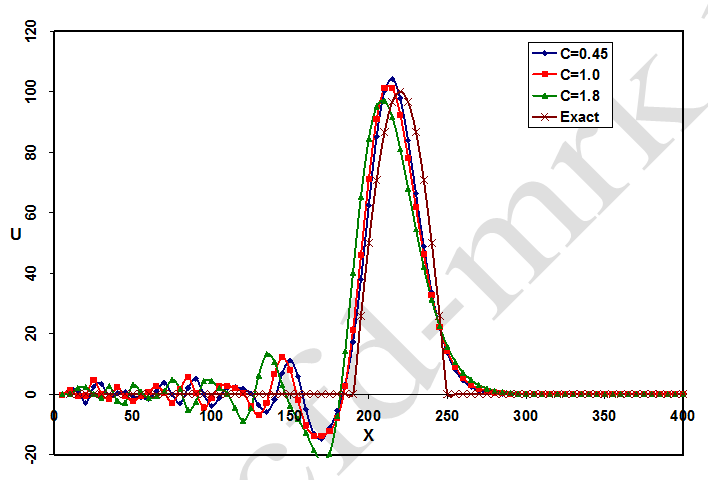
شکل-15: مقایسه بین نتایج بدست آمده از روش ضمنی کرنک-نیکلسون با اعداد کورانت مختلف در زمان t=0.45 S.

همانطور که از شکلهای (14) و (15) پیداست، در روش کرنک-نیکلسون پاسخ‌ها دارای نوسانات قابل توجهی می‌باشد. همچنین، با افزایش زمان میزان خطا نیز افزایش می‌یابد. قابل توجه است که در روش کرنک-نیکلسون قبل از شروع موج دامنه نوسان صفر نبوده و شاهد نوسانات زیادی پیش از شروع در شکل (14) هستیم. علت این امر نیز وجود ترم uⁿ_j-1 در معادلات (33) و (34) می‌باشد. نکته قابل توجه اینست که اگر چه هر قدر مقدار عدد کورانت افزایش یابد در پایداری حل مسئله تأثیری ندارد، اما انتخاب بیش از اندازه بزرگ عدد کورانت موجب کاهش دقت در پاسخهای نهایی می‌شود (شکل15).

حل عددی معادلات هذلولوی مرتبه دوم با روش‌های تفاضل محدود

اساس حل عددی معادله موج مرتبه دوم همانند معادله موج مرتبه اول می‌باشد. برای درک بهتر از چگونگی حل معادله موج مرتبه دوم، مثال-2 ارائه شده است. در این مثال حل عددی یک معادله موج مرتبه دوم یک بعدی با روش جهشی نقطه میانی(Leapfrog Method) [4] مورد بررسی قرار گرفته است.

مثال-2:

معادله موج مرتبه دوم یک بعدی زیر در نظر بگیرید که در آن سرعت صوت است (معادله 35). به منظور حل معادله هذلولوی مرتبه دوم دو دسته شرائط اولیه مورد نیاز است که در این مثال این شرائط به‌ صورت روابط (36) تعریف شده است. همچنین شرائط مرزی که نشان دهنده دیواره جامد می‌باشد در قالب معادلات (37) تعیین شده است.

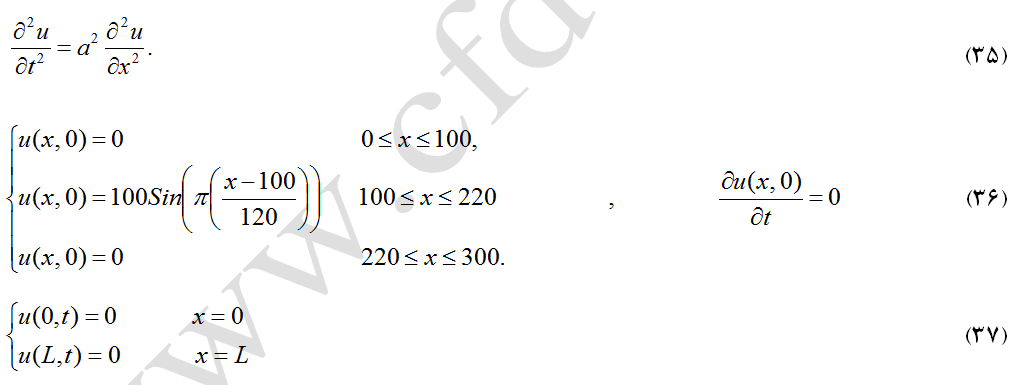
با استفاده از روش جهشی نقطه‌ای میانی، معادله تفاضل محدود متناظر با معادله موج مرتبه دوم یک بعدی در قالب معادله (38) بیان می‌شود. این روش سه مرحله‌ای است، یعنی متغیر وابسته در مراحل زمانی n، n-1 و n+1 ظاهر می‌شود. بهمین خاطر برای شروع روند حل به یک معادله شروع کننده نیاز است. برای یافتن معادله شروع کننده از دومین شرط اولیه استفاده می‌شود(معادله 39). با جایگذاری معادله (39) در رابطه‌ی دوم معادله (38) معادله (40) حاصل می‌شود. همانطور که اشاره شد، معادله (40) تنها یک معادله شروع کننده است و بنابراین تنها برای گام زمانی اول مورد استفاده قرار می‌گیرد (معادله 41).

با محاسبه مقادیر u²_i در تمام ها، دو دسته اطلاعات در n=1 و n=2 خواهیم داشت که با استفاده از آنها و معادله (38) حل عددی معادله موج مرتبه دوم خطی امکان‌پذیر می‌شود. نتایج مربوطه در شکل‌های (16) و (17) نشان داده شده است. موج اولیه به دو موج (هرکدام با دامنه‌های برابر نصف دامنه موج اولیه) با طول موج‌های مساوی تقسیم می‌شود که در دوجهت مشخصه پیشروی می‌کند. از آنجا که امواج روی دیواره منعکس می‌شود، علامت u تغییر می‌کند. به همین خاطر برای روشن بودن شکل، همه مقادیر منفی u در شکل تغییر علامت داده شده و به صورت مثبت رسم شده است. در این مثال برای C=1 جواب دقیق بدست می‌آید. از طرفی از آنجا که مسئله فوق دارای دقت مرتبه دوم می‌باشد، برای C<1 شاهد بروز خطای نوسانی می‌باشیم (شکل‌های 16 الف و 17).

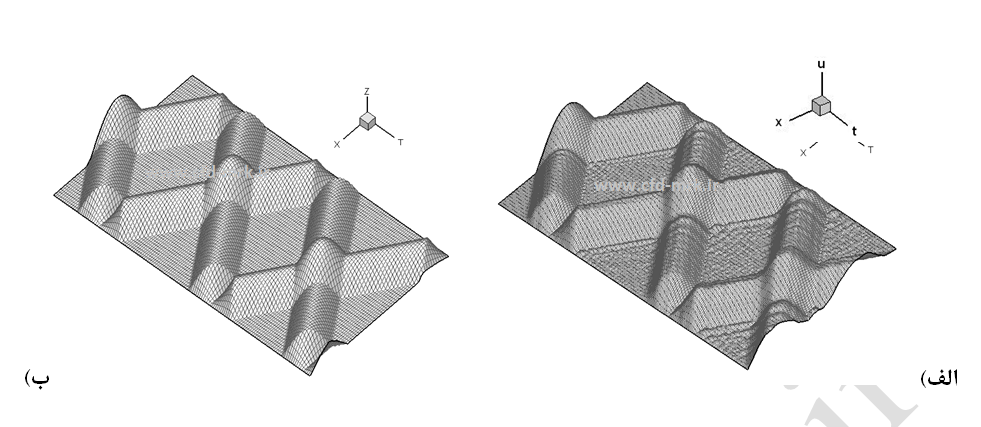
شکل-16: حل معادله موج مرتبه دوم یک بعدی با استفاده از روش جهشی نقطه میانی، الف: C=0.45، ب: C=0.9996.

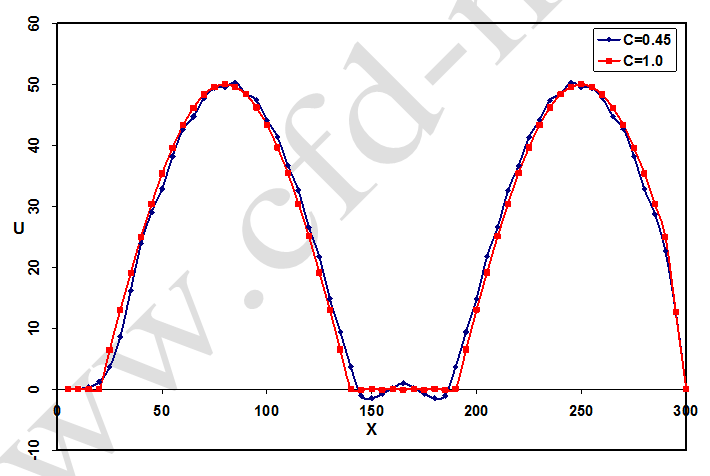
شکل-17: مقایسه بین نتایج بدست آمده از روش ضمنی کرنک-نیکلسون با اعداد کورانت مختلف در زمان t=0.28 S.

-[1]

K. A. Hoffman AND S.T. Chaing, “Computational Fluid Dynamics for Engineer”, Volume 1, Engineering Education System, Wichita, Kansas, 1993

حل معادلات هذلولوی به روش تفاضل محدود