حل معادلات سهموی به روش تفاضل محدود

حل معادلات سهموی به روش تفاضل محدود

Solving Parabolic PDEs Using FDM

بمنظور بررسی روش‌های عددی حل معادلات دیفرانسیل جزئی سهموی، معادلات کلاسیک یک و دو بعدی گرما مد نظر قرار گرفته شده است. روش‌های متعددی در حل معادلات سهموی به روش تفاضل محدود برای فضاهایی یک بعدی (معادله 1و معادله 17) و دو بعدی (معادله 28) وجود دارد که به روش‌های صریح و ضمنی تقسیم‌بندی می‌شود. در این نوشتار، روش‌های مذکور بطور کامل مورد بررسی قرار می‌گیرد.

 

حل عددی معادله سهموی یک بعدی

مثال-1: انتقال حرارت هدایت یک بعدی در طول یک باریکه (Slab) 

بعنوان اولین مثال، انتقال حرارت هدایت در طول یک باریکه (Slab) به طول 0.3 متر که با استفاده از معادله دیفرانسیل جزئی سهموی یک بعدی مدلسازی شده (معادله 17) را در نظر بگیرید. هدف از حل این مسئله تعیین توزیع دمایی روی باریکه در زمان‌های مختلف با استفاده از روش‌های مختلف عددی می‌باشد.

روش‌های صریح (Explicit Methods) برای حل معادلات سهموی به روش تفاضل محدود در یک بعد

برای حل معادلات سهموی به روش تفاضل محدود، الگوریتم‌های متعددی برای گسسته‌سازی صریح معادله توزیع گرما (معادله 17) پیشنهاد شده که روش‌هایی نظیر پیشرو در زمان و مرکزی در مکان، ریچاردسون و دوفورت-فرانکل از مهمترین آنها بشمار می‌رود. در ادامه، این روشها بطور کامل مورد بررسی قرار می‌گیرد.

روش پیشرو در زمان و مرکزی در مکان

در روش تفاضل پیشرو در زمان و مرکزی در مکان (FTCS) به صورت معادله (18) نوشته می‌شود. این معادله (19) از مرتبه [(∆t) و ²(∆x)] می‌باشد. گره‌های محاسباتی درگیر در این روش در شکل (1) نشان داده شده است. جواب‌های بدست آمده برای مثال-1 با استفاده از این روش در شکل‌های (2) و (3) نشان داده شده  است.

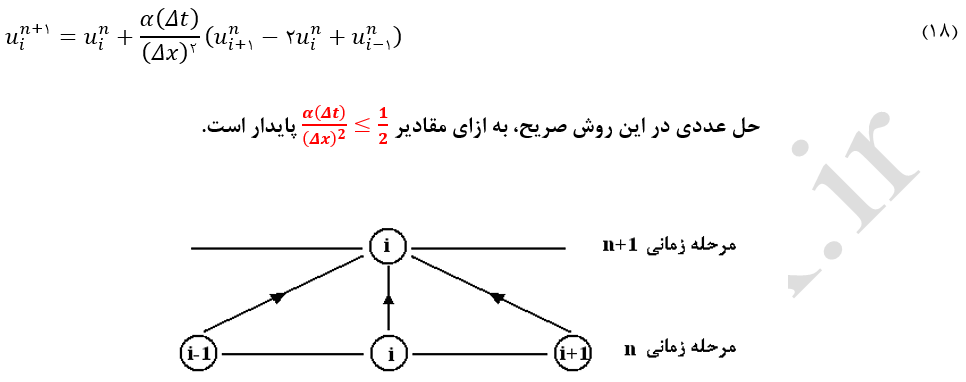
شکل-1: گره‌های محاسباتی درگیر در روش صریح پیشرو در زمان و مرکزی در مکان.

 

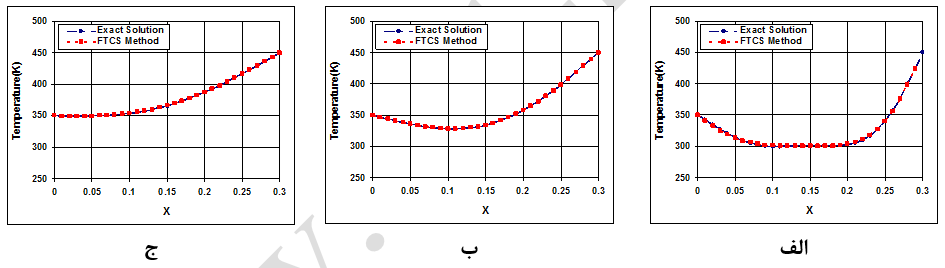
شکل-2: نمودار توزیع دما در امتداد یک باریکه در زمانهای الف: 5 ثانیه، ب: 30 ثانیه و ج: 60 ثانیه (روش FTCS).

نتایج نشان داده شده در شکل فوق حاکی از تطابق دقیق نتایج عددی و تحلیلی می‌باشد. همانطور که در شکل (2-الف) پیداست طول قابل توجهی از باریکه 300 درجه کلوین است. این مهم بخاطر دمای اولیه (شرط اولیه) باریکه است. با گذشت زمان، دما در طول میله افزایش پیدا کرده (شکل‌های 2-ب و ج) تا در نهایت، به حالت تعادل برسد که یک توزیع خطی می‌باشد (شکل 3). طبیعی است که با تغییرات خصوصیات ماده باریکه، زمان به تعادل رسیدن توزیع دما در آن نیز تغییر خواهد یافت. بعنوان مثال، با افزایش ضریب هدایت حرارتی ماده، باریکه در زمان کمتری به دمای تعادل می‌رسد.

 

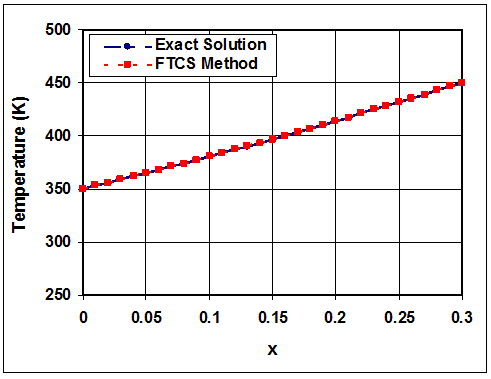
شکل-3: توزیع دمای تعادل در امتداد یک باریکه (در زمان 180 ثانیه).

 

روش ریچاردسون (Richardson Method)

در این روش تقریب تفاضل مرکزی هم برای زمان و هم برای مکان استفاده می‌شود. رابطه جبری پیشنهادی برای این روش بصورت معادله (19) است که از مرتبه [(∆t) ², (∆x)²] برخوردار است. آنالیز پایداری نشان می‌دهد که این روش بی‌قید و شرط ناپایدار بوده و از هیچ مقدار محاسباتی مناسبی برخوردار نیست. نمونه‌ای از نتایج بدست آمده از این روش در شکل (4) نشان داده شده که ناپایداری حل بصورت نوسانات شدید در پاسخ‌ها مشخص است. بنابراین، در حالت کلی روش ریچاردسون به تنهایی هیچ کاربردی در حل عددی معادلات دیفرانسیل جزئی سهموی ندارد.

 

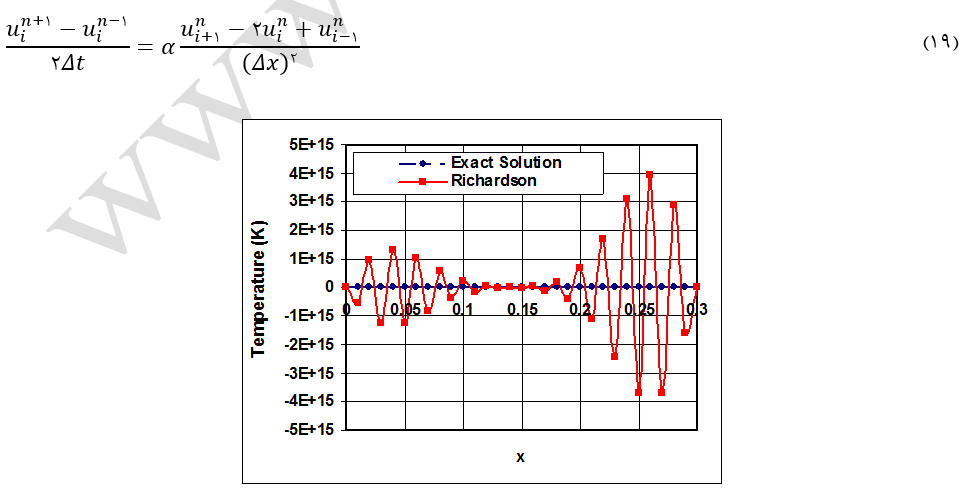
شکل-4: نمودار توزیع دما در امتداد باریکه در زمان 5 ثانیه (روش ریچاردسون).

 

روش دوفورت-فرانکل (DuFort-Frankel Scheme)

در روش دوفورت-فرانکل نیز همانند روش ریچاردسون از تقریب تفاضل مرکزی برای زمان و مکان استفاده می‌شود. با این تفاوت که بجای uⁿ_i  در روش ریچاردسون از مقدار میانگین uⁿ⁺¹_i و u^n-1_i استفاده می‌شود. علت این جایگذاری به خاطر ملاحظات پایداری است. در واقع، این روش همان روش تصحیح شده ریچاردسون است که فرمولاسیون کلی آن بصورت رابطه (20) می‌باشد. معادله مذکور را می‌توان به فرم معادله (21) نیز بازنویسی کرد. با مرتب کردن این معادله، فرم نهایی روش دوفورت-فرانکل در قالب معادله (22) بیان می‌شود.

نتایج بدست آمده از این روش در شکل (5) نشان داده شده است.

 

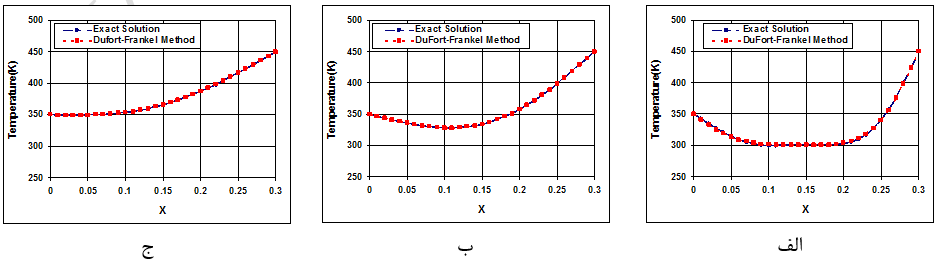
شکل-5: نمودار توزیع دما در امتداد یک باریکه در زمانهای الف: 5 ثانیه، ب: 30 ثانیه و ج: 60 ثانیه (روش دوفورت-فرانکل).

با توجه به فرمولاسیون روش مذکور لازمست در شروع انجام محاسبات، مقدار u_i در گام‌های زمانی n و n-1 معلوم باشد. بنابراین، یا دو مرحله زمانی از داده‌ها باید موجود باشد و یا اینکه در حالتهای خاص (مانند اولین گام زمانی، n+1=1) شروع شده و مقادیر در نظر گرفته شده برای u_i در گامهای زمانی n و n-1 همان مقادیر تعیین شده شرط اولیه باشد. در روش دوفورت-فرانکل دو نکته قابل توجه است. اول اینکه دقت حل با استفاده از این روش به حدس اولیه وابسته است. دوم اینکه، از آنجائیکه در این روش برای انجام محاسبات نتایج، مقادیر متغیرها در دو گام زمانی قبلی نیز مورد نیاز است، لذا حافظه مورد نیاز برای انجام محاسبات بیشتر از سایر روش‌های صریح خواهد بود.

روش‌های ضمنی برای حل معادلات سهموی به روش تفاضل محدود در یک بعد

روش حل معادلات جبری ناشی از گسسته سازی معادلات دیفرانسیل جزئی به صورت یک دستگاه معادلات، به روش ضمنی معروف است. بطور کلی، اگر معادله (17) بصورت معادله (23) گسسته‌سازی شود، آن را روش ضمنی گویند.

روش‌های ضمنی از پایداری بسیار بیشتری نسبت به روش‌های صریح برخوردار بوده و بنابراین در آن‌ها گام‌های زمانی بمراتب بزرگتری نسبت به روش‌های صریح قابل استفاده است. از طرفی، در روش‌های ضمنی در هر زمان (یا تکرار) تعداد گره‌های درگیر در محاسبات و همچنین، عملیات ریاضی مورد نیاز بطور قابل توجهی از روش‌های صریح بیشتر است. البته، این مهم باعث افزایش حافظه مورد نیاز در این روش‌ها می‌باشد. در ادامه مهمترین روش‌های ضمنی قابل استفاده در حل عددی معادله دیفرانسیل جزئی سهموی یک بعدی توضیح داده می‌شود.

 

روش لاسونن (Laasonen Method)

روش لاسونن ساده‌ترین روش ضمنی است که فرمولاسیون آن به صورت معادله (23) می‌باشد. گره‌های درگیر در محاسبات با این روش در شکل (6) نشان داده شده است. با بکارگیری معادله فوق برای تمامی گره‌های شبکه، یک دستگاه معادلات جبری خطی حاصل می‌شود. چگونگی حل این دستگاه در اینجا توضیح داده شده است. همچنین، نتایج بدست آمده از حل مثال-1 با استفاده از این روش در شکل (7) نشان داده شده که همخوانی بسیار خوبی را در مقایسه با نتایج دقیق نشان می‌دهد.

 

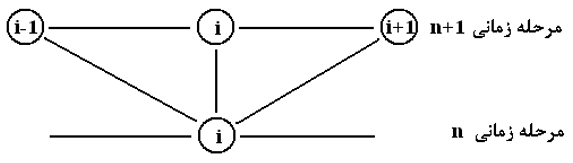
شکل-6: گره‌های محاسباتی درگیر در روش ضمنی لاسونن.

 

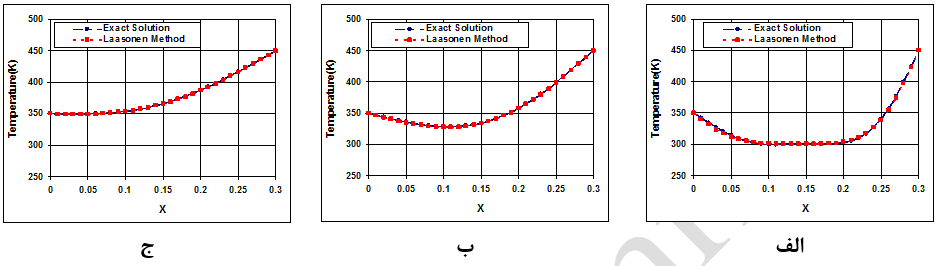
شکل-7: نمودار توزیع دما در امتداد یک باریکه در زمانهای الف: 5 ثانیه، ب: 30 ثانیه و ج: 60 ثانیه (روش لاسونن).

 

روش کرنک-نیکلسون (Cranck-Nicolson)

اگر در روش لاسونن، ترم انتشار در معادله (23) با میانگین تفاضل مرکزی در زمانهای n و n+1 جایگزین شود، فرم گسسته معادله مذکور به رابطه (24) تبدیل می‌شود. با توجه به گره‌های شبکه در شکل (8)، سمت چپ معادله (24) بیانگر تفاضل مرکزی برای گره A است. درحالیکه، سمت راست معادله میانگین ترم انتشار در همان گره است. این روش را می‌توان در قالب دو مرحله محاسباتی و بصورت معادلات (25) و (26) نوشت. معادله (25) بصورت صریح و معادله (26) بصورت ضمنی قابل حل است.

 

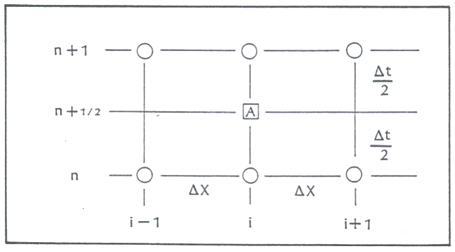
شکل-8: گره‌های درگیر در روش ضمنی کرنک-نیکلسون.

با جمع کردن معادلات (5-25) و (5-26) با یکدیگر همان معادله (5-24) حاصل می‌شود که از مرتبه دوم [²(t∆) و ²(x∆)] می‌باشد. روش مذکور بی‌قید و شرط پایدار است و محدودیتی در مقدار گام زمانی، t∆، وجود ندارد. نتایج بدست آمده از این روش درشکل (9) نشان داده شده که همخوانی بسیار خوبی را با نتایج دقیق نشان می‌دهد.

 

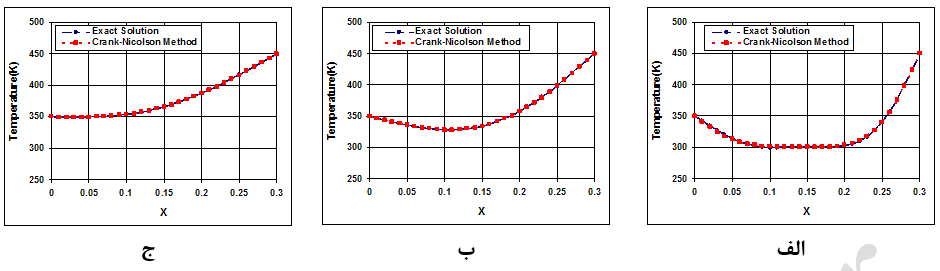
شکل-9: نمودار توزیع دما در امتداد یک باریکه در زمانهای الف: 5 ثانیه، ب: 30 ثانیه و ج: 60 ثانیه (روش کرنک-نیکلسون).

 

فرمولاسیون هیبریدی بتا

معادله (17)  بصورت معادله کلی زیر که ترکیبی از روش‌های صریح و ضمنی است و به فرمولاسیون بتا1 معروف است می‌تواند گسسته شود:

 

می‌توان نشان داد که برای 1/2 ≤ β ≤ 1، این روش بی قید و شرط پایدار است. همچنین در حالت‌های، β = 1/2 روش مذکور معادل روش کرنک-نیکلسون، β = 1 معادل روش لاسونن، 0 ≤β و β ≤ 1/2 بطور مشروط پایدار و در نهایت β = 0 معادل روش FTCS  می‌باشد.  نتایج بدست آمده از این روش در شکل (10) نشان داده شده که همخوانی بسیار خوبی را با نتایج دقیق نشان می‌دهد.

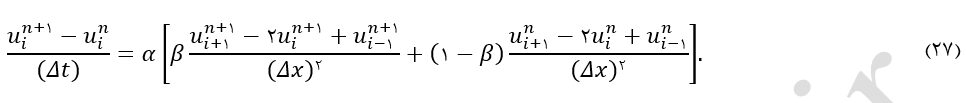
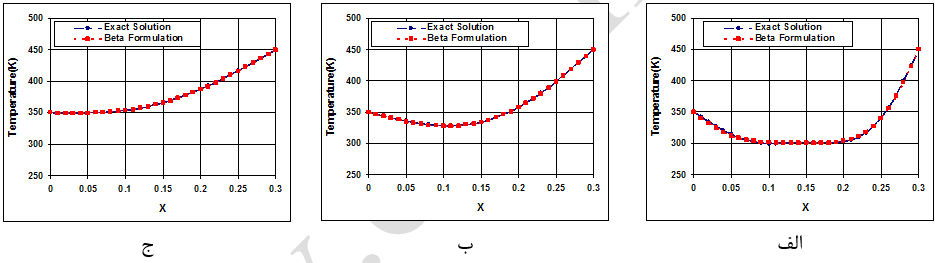
شکل-10: نمودار توزیع دما در امتداد باریکه در زمانهای الف: 5 ثانیه، ب: 30 ثانیه و ج: 60 ثانیه (روش بتا، ).

 

حل عددی معادله سهموی دو بعدی

برای حل عددی معادلات دیفرانسیل جزئی سهموی در فضای دو بعدی، توزیع ناپایای انتقال حرارت هدایت در یک صفحه تخت مورد بررسی قرار گرفته است. فرم کلی انتقال حرارت هدایت دو بعدی ناپایا (معادله دیفرانسیل جزئی سهموی دو بعدی) بصورت معادله (28) می‌باشد.

در معادله فوق،α یک مقدار ثابت است. در ادامه، دو روش FTCS و ADI برای حل عددی این نوع معادلات توضیح داده شده است (مثال-2).

مثال-2: انتقال حرارت هدایت دو بعدی روی یک صفحه

در این مثال، هدف بدست آوردن توزیع دما در حالت ناپایا روی یک صفحه چهار ضلعی دو بعدی می‌باشد. ابعاد صفحه مذکور 1 متر در جهت X و 2 متر در جهت Y در نظر گرفته شده است (شکل11). شرائط مرزی اعمالی روی سطح مذکور عبارتند از:

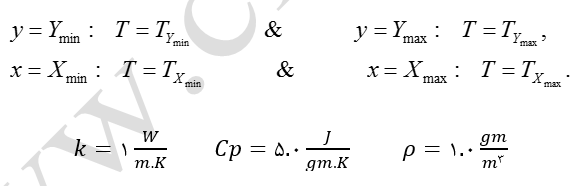
این صفحه که دارای دمای اولیه 300 درجه کلوین است، در یک لحظه ضلع پایینی آن در محیطی با دمای متفاوت 400 درجه کلوین قرار می‌گیرد. هدف محاسبه پروفیل دما در زمانهای 5، 30 و 90 ثانیه می‌باشد.

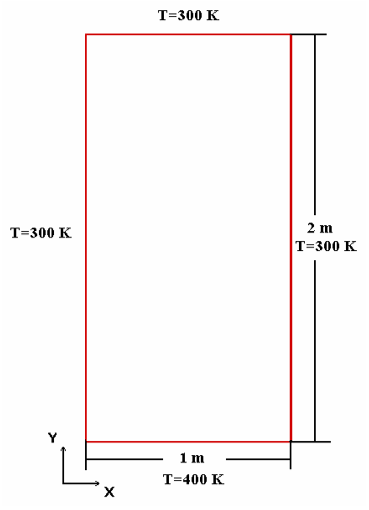
شکل 11: شرائط مرزی مثال 2.

 

روش صریح پیشرو در زمان و مرکزی در مکان

در روش FTCS معادلات بصورت تفاضل پیشرو در زمان و مرکزی در مکان گسسته‌سازی می‌شود. فرم کلی معادله گسسته شده با استفاده از این روش در قالب معادله (29) بیان شده و از مرتبه [(t∆) و ²(x∆) و ²(y∆)] می‌باشد. آنالیز پایداری نشان می‌دهد که روش مذکور تحت شرائط حاکم بر رابطه (30) پایدار است.

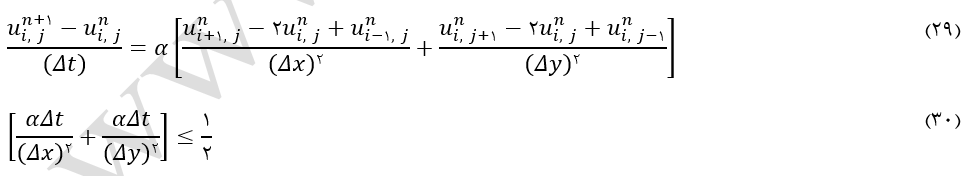
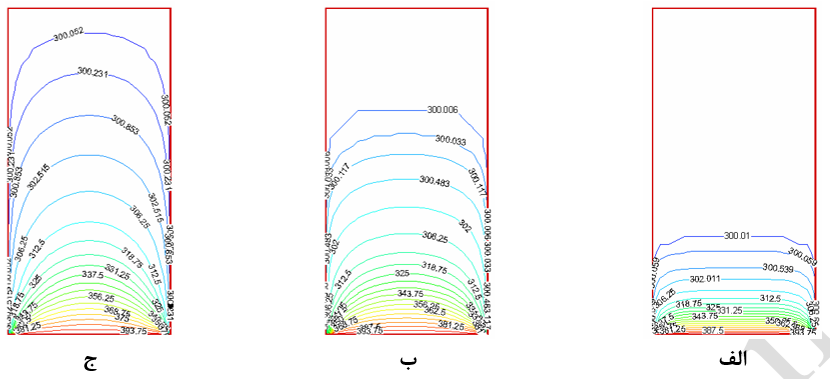
نتایج بدست آمده از این روش در شکل (12) نشان داده شده است.

 

روش ضمنی ADI

در صورت استفاده از فرمولاسیون ضمنی برای گسسته‌سازی معادله سهموی دو بعدی، معادله مذکور بفرم رابطه (31) تبدیل می‌شود که می‌توان آن را همانند معادله (32) مرتب نمود. با نگاهی دقیقتر به معادله (32) می‌توان دریافت که برای حل آن به یک دستگاه معادلات 5 قطری نیاز است. این مهم باعث افزایش حجم محاسبات و پیچیدگی الگوریتم‌های مربوطه می‌شود. بهمین خاطر با استفاده از روش ADI (مبحث معادلات بیضوی و حل دستگاه معادلات خطی) روند حل به دو مرحله تقسیم شده که در این دو مرحله، حل با جاروب کردن مجهولات یک بار در جهت i و یک بار در جهت j  انجام می‌شود. همچنین، در هر مرحله بجای دستگاه معادلات پنج قطری یک دستگاه معادلات سه قطری حل می‌شود. بطور کلی، فرم گسسته معادله (32) با استفاده از فرمولاسیون ADI بصورت روابط (34) و (35) می‌باشد. این روش از مرتبه [(t∆) و ²(x∆) و ²(y∆)] بوده و بی قید و شرط پایدار است. معادلات فوق را می‌توان بفرم ماتریسی و بصورت معادلات (36) و (37) نوشت.

نتایج بدست آمده از این روش برای مثال-2 در شکل (13) نشان داده شده است.

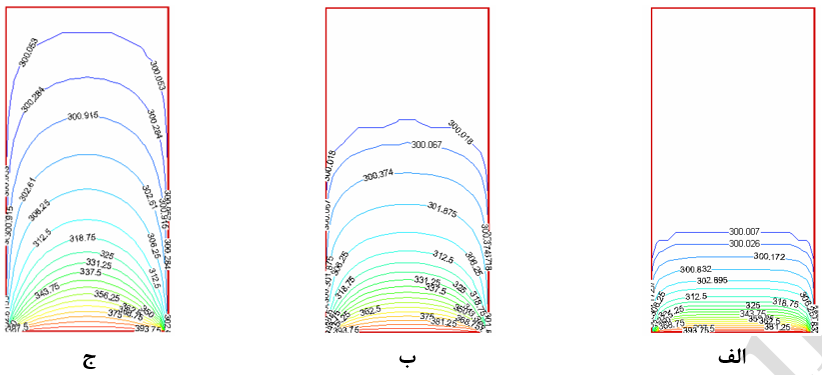
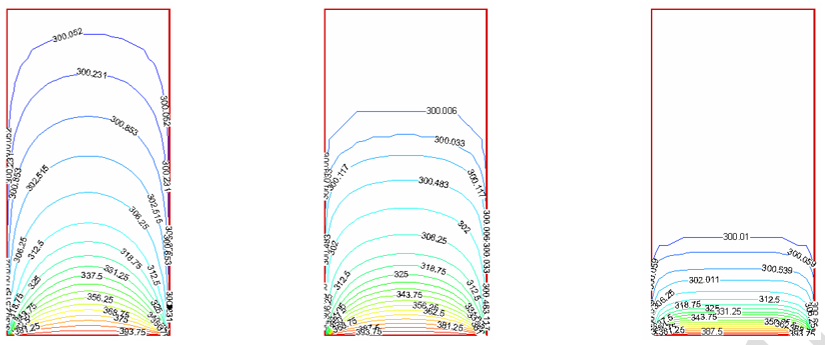
شکل-13: نمودار توزیع دما در روی سطح در زمانهای الف: 5 ثانیه، ب: 30 ثانیه و ج: 90 ثانیه (روش ADI).

 

 

:[1]

Stanley J. Farlow, “Partial Differential Equations for Scientists and engineers”, Dover Publications INC, New York, 1993