معرفی مدل آشفتگی تنش رینولدز (RSM)

Reynolds Stress Turbulence Model: RSM

مدل آشفتگی RSM را می‌توان به عنوان مبسوط ترین و پیچیده‌ترین مدل آشفتگی مبتنی بر روش‌های RANS برشمرد. برخلاف تمامی مدل‌های آشفتگی RANS، مدل RSM از فرضیه بوزینسک (مفهوم لزجت گردابه‌ای) برای حل تنش‌های رینولدز استفاده نمی‌کند بلکه این متغیرها را بطور مستقیم از معادلات انتقالی محاسبه می‌کند. با حذف تئوری لزجت گردابه‌ای همگن (Isotropic Eddy-Viscosity)، این مدل دستگاه معادلات ناویراستوکس متوسط گیری شده (RANS) را با معادلات انتقال برای تنش‌های برشی به همراه یک معادله مناسب برای نرخ اتلاف، می‌بندد. بنابراین برای استفاده از مدل RSM به 5 معادله اضافی(4 معادله برای مؤلفه های تنش رینولدز و یک معادله برای نرخ اتلاف) در دو بعد و 7 معادله اضافی(6 معادله برای مؤلفه های تنش رینولدز و یک معادله برای نرخ اتلاف) در سه بعد نیاز است.

هنوز بطور قطع ثابت نشده است که مدل RSM نسبت به سایر مدل‌های ساده‌تر از برتری بی چون و چرایی در شبیه سازی تمامی رژیم‌های جریان برخوردار باشد تا بتوان هزینه‌های اضافی تحمیل شده از محاسبات گسترده‌تر این مدل را توجیه نمود. اما به هر صورت مهم اینست که استفاده از RSM یک الزام در مواردی است که علاوه بر غیر همگن بودن جریان در تنش‌های رینولدز، پارامترهای دیگری مهم باشند. از جمله این موارد می‌توان به جریان‌های سیکلون، جریان‌های شدید چرخشی در محفظه‌های احتراق، جریان‌های دورانی شدید و جریان‌های ثانویه القائی از تنش (Stress-Induced Secondary Flows) در کانال‌ها اشاره نمود.

ممکن است فرم دقیق معادلات انتقال تنش رینولدز با استخراج ممنتم از معادله دقیق ممنتم بدست آید. این فرآیندی است که در آن معادلات دقیق ممنتم برای نواسانات با سرعت نوسانی ضرب شده و متوسط گیری شود که نتیجه آن همان متوسط گیری رینولدز خواهد بود. متأسفانه وجود چند ترم مجهول در معادله دقیق مستلزم اعمال فرضیاتی در معادله ممنتم شده تا دستگاه معادلات بسته شود و این خود موجب کاهش دقت مدل شود. 

 

 **آموزش تئوری و استفاده از مدل‌ آشفتگی RSM در نرم افزار Fluent همراه با حل یک مسئله**

 

فرمولاسیون مدل آشفتگی RSM

همانطور که گفته شد برخلاف تمامی مدل‌های آشفتگی RANS، مدل RSM مؤلفه‌های تنش برشی را بطور مستقیم از معادلات انتقالی محاسبه می‌کند. فرمولاسیون کلی این معادلات انتقالی به صورت زیر است:

ترم‌های متنوعی در معادله‌ی فوق وجود دارند از این ترم‌ها، ترم‌های جابجایی (Convection)، انتشار ملکولی (Molecular Diffusion)، تولید تنش Stress Production و ترم تولید ناشی از دوران سیستم (Production by System Rotation) به مدلسازی نیازی ندارند اما ترم‌های انتشار آشفته (Turbulent Diffusion)، تولید بویانسی (Buoyancy Production)، کرنش فشاری (Pressure Strain) و اتلاف (Dissipation) به معادلات اضافی دیگری برای بستن دستگاه معادلات حاکم بر جریان نیاز دارند. 

در فرمولاسیون فوق مدلسازی ترم‌های کرنش فشاری (Pressure Strain)  و نرخ اتلاف (Dissipation) اصلی‌ترین چالشهای محاسباتی مدل RSM بوده و اغلب باعث کاهش دقت پیش بینی‌های آن می‌شوند. نکته قابل توجه اینجاست که حتی مدل RSM نیز برای معادله مقیاس یا همان معادله انتقالی نرخ اتلاف (یا اتلاف ویژه) -که در رابطه بالا بصورت εij≡Dissipation  نمایش داده شده است- به معادلات انتقالی ترم اتلاف (ε:Epsilon) یا اتلاف ویژه (ω:Omega) مدل‌های آشفتگی K-Epsilon (یا K-Omega) وابسته بوده و بنابراین طبیعی است که میراث دار نواقص ناشی از مفروضات اساسی این معادلات باشد.

در مدل RSM مبتنی بر Epsilon، معادلاتی نظیر مدل کرنش فشاری خطی (Linear Pressure-Strain Model) و یا مدل کرنش فشاری مربعی (Quadratic Pressure-Strain Model) برای محاسبه کرنش فشاری فشاری توسعه یافته و در نرم افزاهایی نظیر Fluent و OpenFoam استفاده می‌شوند. همچنین برای محاسبه نرخ اتلاف ویژه در مدل RSM با استفاده از مدل K-Omega (مدل RSM مبتنی بر Omega) دو معادله Stress-Omega Model و Stress-BSL Model در دسترس می‌باشد که در نرم افزار Fluent نیز از آن‌ها استفاده می‌شود.

 

مدلسازی انتقال پراکنده آشفته (Modeling Turbulent Diffusive Transport)

برای مدل‌های RSM مبتنی بر Epsilon، ترم انتشار آشفته با تعمیم سازی مدل انتشار-گرادیان (Gradient-Diffusion) دالی (Daly) و هارلو (Harlow) بدست می‌آید. 

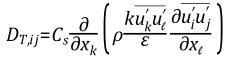
قابل توجه است که معادله فوق می‌تواند ناپایداری‌های عددی را به دنبال داشته باشد. لذا می‌توان از فرم ساده شده زیر استفاده کرد (کاری که در نرم افزار Fluent انجام شده است).

نحوه محاسبه μt همانند همان رابطه استفاده شده در مدل K-ε Standard (رابطه هدف از مدل K-ε Standard) می‌باشد. لین (Lien) و لشزینر (Leshziner) مقدار σk=0.82 را برای مدل انتشار گرادیان تعمیم یافته برای حالت جریان برشی همگن صفحه‌ای پیشنهاد کردند. توجه داشته باشید که این مقدار σk با مقدار معادل آن در مدل K-Epsilon (که برابر یک می‌باشد) متفاوت است.

برای مدل‌های RSM مبتنی بر Omega هم از رابطه مدل اصلاح شده انتشار آشفته  استفاده می‌شود  و لزجت آشفتگی نیز از رابطه μt تعریف شده برای مدل استاندارد k-ω (رابطه هدف از مدل K-ω Standard) محاسبه می‌گردد. همچنین σk در این حالت برابر با 2 می‌باشد اما اگر از مدل RSM مبتنی بر Omega-BSL استفاده شود مقدار σk بر اساس تابع وزنی F1 بین σk,1=2 و σk,2=1 متغیر خواهد بود و در واقع رابطه نشان داده شده در بالا برای محاسبه σk بکار گرفته می‌شود. 

 

مدلسازی ترم کرنش فشاری (Modeling the Pressure-Strain Term)

رابطه مناسب برای مدلسازی کرنش فشاری، φij، بسته به نوع معادله انتقالی در نظر گرفته شده برای نرخ اتلاف (اتلاف ویژه) متفاوت است. از مهمترین مدل‌های محاسبه کرنش فشاری می‌توان به موارد زیر اشاره نمود:

برای مدل‌های RSM مبتنی بر Epsilon  

• مدل کرنش فشاری خطی (Linear Pressure-Strain Model)
• مدل کرنش فشاری مرتبه دوم (Quadratic Pressure-Strain Model)

برای مدل‌های RSM مبتنی بر Omega 

• مدل تنش امگا (Stress-Omega Model)
• مدل Stress-BSL

مدل کرنش فشاری خطی (Linear Pressure-Strain Model)

در این مدل که گزینه پیش‌فرض مدل RSM بکار رفته در نرم افزار Fluent نیز می‌باشد، ترم کرنش فشاری براساس پیشنهادات گیبسون (Gibson) و لاندر (Launder)، فو (Fu) و همکارن و فعالیت مستقل لاندر، مدلسازی شده است. رابطه کلاسیک محاسبه کرنش فشاری در این مدل بصورت زیر می‌باشد:

در روابط فوق

• φij,1: کرنش فشاری کند (Low Pressure-Strain) که به عنوان ترم بازگشت به ایزوتروپی نیز شناخته می‌شود، 
• φij,2: کرنش فشاری سریع (Rapid Pressure-Strain)، 
• φij,w: ترم انعکاس دیواره،
• nk: مؤلفه kام از بردار واحد عمود بر دیواره،
• d: فاصله عمود بر دیواره و 
• k=0.4187: ثابت ون کارمن (Von Karman) می‌باشند. 

ترم φij,w مبین بازتوزیع (Redistribution) تنش‌های عمودی نزدیک دیواره می‌باشد. رفتار این ترم به گونه‌ای است که با تقویت تنش‌های موازی با دیواره، تنش‌های عمود بر دیواره کاهش یافته و تضعیف می‌گردد. لازم به توضیح است این ترم بطور پیش فرض در نرم افزار Fluent فعال می‌باشد. 

اصلاحات عدد رینولدز پایین برای مدل کرنش فشاری خطی ( Low-Re Modifications to the Linear Pressure-Strain Model)

در استفاده از مدل RSM هنگامیکه محاسبه مقدار للزجت در زیر لایه ویسکوز (Viscous Sub Layer) مد نظر باشد (به عبارت دیگر هنگامیکه از روش دولایه‌ای، Two Layer Model، برای محاسبه لزجت استفاده شود) لازمست مدل کرنش فشاری خطی مدل RSM مبتنی بر Epsilon تصحیح گردد. این اصلاحیه‌ها در مورد ثابت‌های مدل کرنش فشاری خطی ارائه شده در بالا و بصورت زیر می‌باشد:

قابل توجه است که در نرم افزار Fluent می‌توان این اصلاحات را زمانیکه گزینه Enhanced Wall Treatment در مدلسازی کرنش فشاری خطی (برای مل RSM مبتنی بر Epsilon) فعال باشد بکار برد. 

مدل کرنش فشاری مرتبه دوم (Quadratic Pressure-Strain Model)

یک مدل کرنش فشاری مرتبه دوم توسط اسپزیال (Spezial)، سرکار (Sarkar) و گاتسکی (Gatski)  به دنیای CFD معرفی شد. این مدل برای عملکرد بهتر مدل آشفتگی RSM برای جریان‌های برشی اصلی شامل کرنش صفحه‌ (Plane Strain)، تنش صفحه دوران (Rotating Plane Shear) و همچنین انبساط/انقباض متقارن محوری (Axisymmetric Expansion/Contraction) مورد بررسی و ارزیابی  قرار گرفته و مشخص شد که از افزایش دقت مناسبی بهره‌مند است. این افزایش دقت برای گستره وسیع‌تری از رژیم‌های جریان‌های پیچیده در مسائل مهندسی بویژه جریان‌هایی که با ممنحنی‌های خطوط جریان سرو کار دارند بسیار مناسب است. فرمولاسیون کلی مدل مذکور بصورت زیر می‌باشد:

در معادلات فوق

• bij: تانسور غیر همگن (Anisotropy) تنش رینولدز،
• Sij: نرخ کرنش متوسط و 
• Ωij: تانسور نرخ دوران متوسط می‌باشند.

مدل کرنش فشاری مرتبه دوم نیازی به تصحیح مقدار اثرات انعکاسی دیواره برای رسیدن به پاسخ‌های قابل قبول در ناحیه لگاریتمی یک لایه مرزی آشفته ندارد. به هر حال باید توجه داشت که این مدل تا زمانیکه گزینه (Enhanced Wall Treatment) در نرم افزار Fluent انتخاب نگردد در دسترس نمی‌باشد. همچنین اصلاحات مرتبط با عدد رینولدز پایین برای این مدل کاربردی ندارد. 

مدل تنش امگا (Stress-Omega Model)

مدل تنش امگا (Stress-Omega Model) یک مدل RSM مبتنی بر معادلات Omega و مدل LRR می‌باشد. این مدل یک مدل ایده‌آل برای شبیه سازی جریان‌های عبوری از سطوح خمیده و جریان‌های چرخشی می‌باشد. فرمولاسیون کلی مدل مذکور بصورت زیر است:

این مدل در پیش بینی مناسب طیف وسیعی از جریان‌های آشفته همانند مدل k-Omega می‌باشد. همچنین اصلاحات مورد نیاز عدد رینولدز پایین و شرایط مرزی سطوح زبر نیز همانند مدل k-omega است. در روابط بالا Sij: مشابه نرخ کرنش متوسط تعریف شده در قسمت قبل بوده و ∗β و ∗fβ همانند ترم‌های اتلاف k و ω در مدل k-Omega محاسبه می‌شود با این تفاوت که در رابطه مرتبط با ∗fβ، کافیست بجای عدد 680، مقدار 640 قرار داده شود. با افزایش دقت مدل در شبیه سازی زیر لایه ویسکوز بااستفاده از تابع جایگزین میرایی لزجت (جایگزینی بجای ) می‌توان قابلیت شبیه سازی این مدل را برای جریان‌های خاص بهبود بخشید. در نرم افزار Fluent اینکار با فعال کردن گزینه Low-Re Correction در گادر محاوره‌ای Viscous Model انجام می‌شود.

مدل Stress-BSL

در مدل RSM مبتنی بر تنش BSL، معادله مقیاس نرخ اتلاف همان معادله ω در مدل K-Omega BSL می‌باشد. بنابراین حساسیت مشاهده شده در مدل Stress-Omega را برای شبیه سازی جریان‌های آزاد نخواهد داشت. فرمولاسیون این مدل نیز دقیقا همانند معادله φij در مدل Stress-Omega (قسمت قبل) اما بدون تصحیحات عدد رینولدز پایین می‌باشد. همچنین در این مدل می باشد. 

 

مدلسازی ترم تولید بویانسی (Buoyancy Production) 

ترم‌های تولید ناشی از بویانسی طبق روابط زیر محاسبه می‌شود:

در رابطه فوق Prt عدد پرانتل آشفتگی بوده و مقدار پیش فرض آن 0.85 در نظر گرفته شده است. با استفاده از تعریف انبساط حرارتی، β=-1/ρ(∂ρ/∂T)p، ترم تولید بویانسی برای گازهای ایده‌آل از طرق معادله آخر نشان داده شده در بالا محاسبه می‌گردد. باید توجه داشته باشید در نسخه‌های مختلف نرم افزار Fluent اثرات بویانسی برای مدل‌ های آشفتگی RSM مبتنی بر Omega در دسترس نیست.

 

مدلسازی انرژی جنبشی آشفتگی

در حالت کلی زمانیکه به محاسبه انرژی جنبشی آشفتگی برای هر ترمی نیاز باشد از رابطه زیر استفاده می‌شود:

همانطور که توضیح داده شد، در شرایط مرزی دیواره یک گزینه برای مدل‌های RSM مبتنی بر Epsilon به منظور حل معادله انتقال انرژی جنبشی آشفتگی با هدف محاسبه شرایط مرزی مناسب دیواره برای مدل RSM وجود دارد که بصورت زیر تعریف می‌شود:

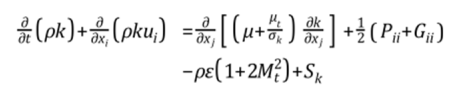
که σk=1.0 و Sk ترم چشمه تعریف شده توسط کاربر می‌باشد. با حل معادله فوق، مقدار K به دست آمده تنها برای شرایط مرزی استفاده می‌شود اما در بقیه حالات K از رابطه معروف نشان داده شده در ابتدای این قسمت محاسبه می‌شود. در هر صورت مقدار K به دست آمده از هر دو روش به یکدیگر نزدیک است. 

 

مدلسازی ترم اتلاف (Modeling the Dissipation Rate)

تانسور نرخ اتلاف، εij، برای مدل‌های RSM مبتنی بر Epsilon یا Omega از روابط جداگانه‌ نشان داده شده در زیر محاسبه می‌شوند:

در روابط فوق:

• YM: یک ترم اضافه اتلاف اتساع (Dilatation Dissipation) مطابق با مدل Sarkar،
• Mt: عدد ماخ آشفته
• α: سرعت صوت و
• ε: مقدار اسکالر نرخ اتلاف می‌باشند.

همچنین برای مدل‌های RSM مبتنی بر Omega، تانسور تنش برشی، εij، بسته به اینکه از چه مدلی (Omega یا BSL) استفاده شود از روابط متناسب در مدل‌های K-Omega Standard یا K-Omega BSL استفاده می‌کند. همچنین باید توجه داشت که لزجت آشفتگی μt در مدل‌های RSM مبتنی بر Epsilon از رابطه تعریف شده برای محاسبه μt در مدل K-Epsilon Standard و در مدل‌های RSM مبتنی بر Omega از رابطه تعریف شده برای محاسبه μt در مدل K-Omega Standard محاسبه می‌شود.

 

مدلسازی انتقال حرارت جابجایی و جرم (Convective Heat and Mass Transfer Modeling)

معادله انتقال حرارت با استفاده از مفهوم آنالوژی رینولدز برای انتقال ممنتم و بصورت زیر تعریف می‌شود:

در رابطه فوق

• E انرژی جنبشی کل و 
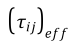• تانسور تنش انحرافی (Deviatoric Stress Tensor) می‌باشد.

ترم تنش انحرافی بیانگر گرمایش لزجت (Viscous Heating) می‌باشد که همیشه در فروملاسیون حلگرهای چگالی مبنا بطور مستتر وجود دارد اما برای حلگرهای فشار مبنا لازمست تعریف شود. (اینکار در نرم افزار Fluent با انتخاب گزینه Viscous Heating در کادر محاوره‌ای Viscous Model انجام می‌شود). در روابط فوق مقدار پیش فرض عدد پرانتل آشفته، Prt،  برابر 0.85 بوده که در صورت لزوم می‌توان آن را تغییر داد. 

انتقال جرم آشفته نیز به طریق مشابه و با پیش فرض عدد آشفتگی اشمیت (Schmidt) برابر 0.7 بدست می‌آید که این عدد آشفتگی را می‌توان در مواقع لازم تغییر داد.

 

شرایط مرزی دیواره

مدل RSM به شرایط مرزی مخصوصی برای تنش رینولدز و نرخ اتلاف آشفتگی (ε یا ω) نیازمند استو این مقادیر می‌تواند مستقیما یا مشتق شده از مقدار شدت آشفتگی یا طول مشخصه بدست آید. نرم افزاری مانند Fluent مقادیر تنش رینولدز و ε  نزدیک به دیواره را از توابع دیواره محاسبه می‌کند. این نرم افزار مستقیما شرایط مرزی دیواره برای تنش‌های رینولدز را با استفاده از قانون لگاریتمی و فرض تعادل صرف نظر از جابجایی و انتشار در معادلات انتقال تنش‌ها بکار می‌گیرد. در واقع در این نرم افزار  با استفاده از سیستم مختصات محلیف جائیکه τ مولفه مماس، η مولفه عمود و λ مولفه نیمه عمود می‌باشند تنش‌های رینولدز در سلول‌های مجاور دیواره و از روابط نشان داده شده در زیر محاسبه می‌شوند. 

برای محاسبه K معادله انتقالی تعریف شده برای K (انرژی جنبشی آشفتگی) در قسمت قبل حل می‌شود. به دلیل راحتی محاسباتی، این معادلات برای کل دامنه محاسباتی علی رغم اینکه K تنها برای المان‌های مجاور دیواره مورد نیاز است، حل می‌شود. در مرزهای بی‌نهایت یا دور دست (Far Field)، مقدار K مستقیما از رابطه اول ارائه شده در قسمت قبل (مدلسازی انرژی جنبشی آشفتگی) محاسبه می‌شود. طبق پیش فرض، مقادیر نزدیک به دیواره تنش‌های رینولدز با استفاده از معادله زیر محاسبه و ثابت شده و معادلات انتقال تنش رینولدز تنها برای ناحیه جریان غالب (Bulk Flow) حل می‌شود.

از سویی دیگر تنش‌های رینولدز مستقیما از ترم‌های تنش برشی دیواره (معادله دوم نشان داده شده در بالا) بجای K بدست می‌آید. با استفاده از معادله تنش برشی دیواره دیگر نیازی به حل معادله K نیست. همچنین با انتخاب گزینه Enhaced Wall در نرم افزار Fluent، شارهای صفر برای معادلات تنش رینولدز در مرزها، در نظر گرفته می‌شود.

 

موارد کاربرد مدل RSM

از آنجائیکه مدل RSM در محاسبات مرتبط با اثرات انحنای خطوط جریان (Streamline Curvature)، چرخش (Swirl)، دوران (Rotation) و تغییرات سریع نرخ کرنش بطور چشمگیری جامع‌تر و دقیق‌تر عمل می‌کند لذا، از پتانسیل به مراتب بیشتری برای شبیه سازی دقیق‌تر جریان‌های پیچیده از جمله جریان‌های شدید دورانی و چرخشی برخوردار است . به هر صورت همچنان اعتبار شبیه سازی‌ها و پیش بینی‌های مدل RSM تحت تأثیر فرضیات محاسبه ترم‌های مختلف موجود در معادلات انتقالی تنش‌های رینولدز می‌باشد.

 

 **آموزش تئوری و استفاده از مدل‌ آشفتگی RSM در نرم افزار Fluent همراه با حل یک مسئله**

 

بازگشت

مطالب مرتبط

حل میدان‌های جریان‌های غیر لزج، آرام و آشفته با استفاده از نرم‌افزارهای CFD

مدلسازی آشفتگی با استفاده از روش‌های RANS

مدلسازی آشفتگی با استفاده از روش‌های LES

مدل‌های آشفتگی ترکیبی SAS و DES

 

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ