مدل تشعشع DO

مدل تشعشع DO

Discrete Ordinates (DO) Radiation Model Theory

مدل تشعشع DO معادله انتقال تابشی(Radiative Transfer  Equation (RTE)) را برای تعداد محدودی از زوایای گسسته‌شده حل می‌کند. هریک از این زوایای گسسته‌شده با یک بردار جهت S مشخص شده در سیستم مختصات کارتزین، متناظر است. اندازه زوایای گسسته‌شده توسط کاربر مشخص می‌شود. این کار همانند انتخاب تعداد پرتوها برای مدل DTRM می‌باشد. اما برخلاف مدل DTRM، مدل DO پرتوها را مسیریابی نمی‌کند. درعوض، معادله RTE را به یک معادله انتقالی برای سیستم مختصات کارتزین تبدیل کرده و در نهایت شدت تابش را محاسبه می‌کند. در واقع مدل DO تمامی معادلات انتقالی را در تمام جهت‌های بردار S حل می‌کند.

روش حل در این مدل همانند روش حل معادلات ممنتم و انرژی حاکم بر سیال است. این مدل بصورت مجزا و کوپل شده با معادلات حاکم بر جریان حل می‌شود. معادلات مدل مذکور بصورت حجم محدود گسسته‌سازی و حل می‌شوند. البته مدل یاد شده برای شبکه‌های بی‌سازمان نیز قابل استفاده است. لازم به ذکر است روش کوپل شده از سرعت/نرخ همگرایی و در عین حال حافظه مورد نیاز بیشتری نسبت به روش مجزا برخوردار می‌باشد.

مدل DO تمام ضخامتهای اپتیکی را پوشش می‌دهد. در تابش سطح-به-سطح برای وارد کردن انتقال حرارت تابشی و در مسائل احتراق نیز می‌توان از این مدل استفاده کرد. همچنین مدل DO تابش پوشش‌های نیمه‌شفاف را هم شبیه‌سازی می‌کند. مدل DO استفاده شده در نرم‌افزار  FLUENT تنها برای تابش خاکستری و تابش غیرخاکستری (با استفاده از مدل باند خاکستری) کاربرد دارد. با افزایش تعداد زوایای گسسته، هزینه محاسبات و حافظه مورد نیاز بطور متناسب و نسبتاً کم افزایش پیدا می‌کند. حل مسائل همراه با افزایش گسسته‌سازی زاویه‌ای CPUهای قدرتمندی را می‌طلبد.

تئوری و معادلات مدل تشعشع DO

در مدل DO، معادله RTE در جهت بردار S و همانند یک معادله میدان حل می‌شود. بنابراین معادله RTE بصورت رابطه (1) بازنویسی می‌گردد. نرم افزارهای CFD نظیر Ansys Fluent از توانایی شبیه سازی تابش غیر خاکستری (Non-Gray) با استفاده از مدل باند خاکستری (Gray-Bond) برخوردار هستند. در این شرایط معادله RTE برای تعیین شدت طیفی I_λ بصورت معادله (2) نوشته می‌شود. فرض بر اینست که ضریب پراکنش (Scattering Coefficient)، تابع فاز پراکنش (Scattering Phase Function) و ضریب شکست یا انکسار (Refractive Index)، مستقل از طول موج هستند.

در مدلسازی غیر خاکستری با استفاده از مدل DO، طیف تابش به N باند طول موج تقسیم می‌شود که نیازی نیست به هم پیوسته یا هم اندازه باشند. بازه‌های طول موج توسط کاربر قابل تنظیم است. البته مقدار ضریب شکست در خلاء همواره برابر با یک، n=1، است. از معادله RTE روی هر بازه طول موج انتگرال‌ گرفته می‌شود و در ادامه معادلات انتقالی برای I_λΔλ و انرژی تابشی موجود در طول موج Δλ بدست می‌آید. نکته مهم آنست که رفتار در هر باند، خاکستری فرض می‌شود. تشعشع جسم سیاه در هر طول موج بر واحد زاویه بصورت معادله (3) تعریف می‌شود. شدت تابش کل نیز از معادله (4) محاسبه می‌شود.

شرط مرزی برای مدل DO غیر خاکستری در مرزهای هر باند اعمال می‌شود. البته رفتار آن در درون هر باند همانند روش مدل Do خاکستری می‌باشد.

کوپلینگ معادلات انرژی و مدل تشعشع DO

کوپلینگ بین انرژی و شدت تابش در هر سلول یا همان COMET باعث افزایش نرخ همگرایی در روش‌های حجم محدود برای حل انتقال حرارت تابشی می‌شود. این روش بطور قابل توجهی موجب بهبود همگرایی در مسائل متشکل از ضخامت نوری بزرگتر از 10 می‌شود. کوپلینگ معادله انرژی و مدل DO در حل مسائل ذوب شیشه بسیار مؤثر است. در و اقع این ویژگی در زمان‌هایی که پراکنش قابل توجه و کوپلینگ قدرتمندی بین شدت‌های تابش سمتی (Directional Radiation) وجود دارد، دارای مزیت است. معادلات انرژی گسسته برای روش کوپلینگ بصورت معادله (5) نوشته می‌شود. زمانیکه معادله انرژی روی حجم کنترل i انتگرال گیری می‌شود، معادله گسسته شده (5) را نتیجه می‌دهد.

محدودیت‌های کوپلینگ معادلات انرژی و مدل تشعشع DO

در موارد زیر شاهد ناسازگاری یا بروز مشکلات در استفاده از کوپلینگ معادلات انرژی و مدل DO هستیم.

• کوپلینگ معادلات انرژی/DO برای مسائلی که از همبستگی ضعیفی بین انرژی و شدت‌های تابش سمتی برخوردار هستند، توصیه نمی‌گردد. این مهم باعث کاهش سرعت همگرایی و افزایش زمان و هزینه محاسبات نسبت به حل متوالی و پشت سر هم (Sequential) این معادلات خواهد شد.
• کوپلینگ معادلات انرژی/DO در هنگام حل معادلات آنتالپی بجای معادلات دما امکان‌پذیر نیست.
• کوپلینگ معادلات انرژی/DO با مدل‌های احتراق غیر پیش آمیخته (Non-Premixed Combustion) و پیش آمیخته جزئی Partially-Premixed Combustion) سازگار نیست.

 

گسسته‌سازی زاویه‌ای و پیکسل‌بندی (Angular Descretization and Pixelation)

هر یک هشتم فضای زاویه‌ای 4π در هر موقعیت مکانی بصورت N_θ*N_ϕ زاویه و به اندازه ω_i که به زوایای کنترل معروف است، گسسته‌‌سازی می‌شود. زوایای θ و ϕ همان زوایای قطبی (Polar) و سمتی (Azimuthal) بوده و نسبت به دستگاه مختصات کارتزین اندازه‌گیری می‌شود (شکل-1). θ و ϕ وسعت زاویه‌ کنترل را معین می‌کند در حالیکه ‌Δθ و‌‌‌ Δϕ ثابت است. در محاسبات دو بعدی، بعلت تقارن، تنها چهار ناحیه یک هشتم حل شده که در مجموع 4*N_θ*N_ϕ را شامل می‌شود. در محاسبات سه‌بعدی، بطور کلی 8*N_θ*N_ϕ حل می‌شود.

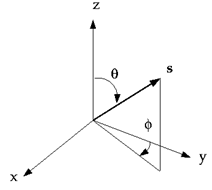
شکل-1: سیستم مختصات زاویه‌ای.

در صورت استفاده از شبکه‌های باسازمان، امکان مرتب‌سازی گسسته‌سازی زاویه‌ای با وجه حجم کنترل، همانند شکل(2) وجود دارد. اما بطور کلی برای شبکه‌های بی‌سازمان این امکان وجود نداشته (شکل-3) و مسئله به یک مسئله Control Angle Overhang : CAO تبدیل می‌شود.

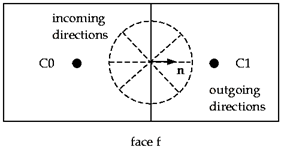
شکل-2: وجه بدون CAO (دو بعدی).

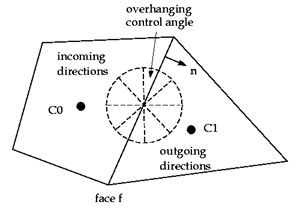
شکل-3: وجه همراه با CAO (دو بعدی).

اساساً زوایای کنترلی می‌تواند بگونه‌ای روی وجوه حجمهای کنترل قرارگیرد که جزئی از آن در ورودی و جزء دیگر آن در خروجی وجه واقع شود. در شکل (4) یک مثال سه بعدی از یک وجه بهمراه CAO نشان داده شده است.

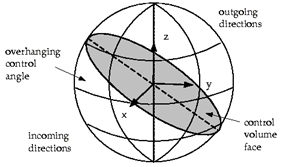
شکل -4: وجه همراه با CAO (سه بعدی).

وجه حجم کنترل، کره متناظر فضای زاویه‌ای در هر زاویه دلخواه را قطع می‌کند. در این حالت، خط تقاطع یک دایره خواهد بود. همچنین CAO ممکن است بصورت نتیجه انعکاس و انکسار رخ دهد. در این موارد مهم است که زاویه کنترل برآمدگی (CAO) به درستی محاسبه شود. محاسبه این پارامتر با پیکسل بندی زاویه‌ای انجام می‌شود. در همین راستا هر زاویه کنترل، ω_i، به N_θP*N_ϕP پیکسل (شکل-5) تقسیم می‌شود.

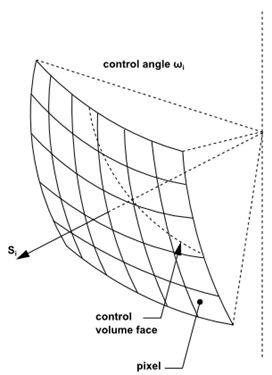
شکل-5: پیکسل بندی هر زاویه کنترل ω_i.

هر پیکسل دارای یک سطح انرژی بوده که می‌تواند به آن وارد شده یا از آن خارج شود. در واقع هر پیکسل از یک شار انرژی برخوردار است. بنابراین اثر برآمدگی (Overhang) می‌تواند در وضوح پیکسل بندی لحاظ گردد. نرم افزار Fluent این امکان را به کاربر می‌دهد تا وضوح پیکسل‌ها را انتخاب کند. برای مسائل درگیر با تابش تشعشع-خاکستری، معمولا رزولوشن پیکسل‌ها 1*1 است. برای مسائل درگیر با شرایط مرزی متقارن، متناوب (پریودیک)، نیمه شفاف (Semi-Transparant)، آینه‌ای یا تک جهته (Specular) رزولوشن 3*3 برای هر پیکسل پیشنهاد می‌گردد. لازم به ذکر است که افزایش رزولوشن مستلزم افزایش هزینه و زمان محاسبات می‌باشد.

پراکنش غیر همگن (Anisotropic Scattering)

اجرای مدل DO در نرم افزارهایی مانند Fluent با انواع توابع مرتبط با فاز پراکنش سازگار است. می‌توان از تابع فاز همگن، خطی، غیر خطی، دلتا-ادینگتون (Delta-Eddington) و یا تعریف شده توسط کاربر (UDF) استفاده نمود.

تابع فاز غیر همگن خطی در معادله (10) و تابع فاز دلتا-ادینگتون در معادله (11) تعریف شده است. در معادله (10) S بردار یکه در جهت پراکندگی و ‘S بردار یکه در جهت پدیده تابش می‌باشد.  C نیز ضریب تابع فاز غیر همگن خطی بوده که جزء خصوصیات سیال است. مقدار این ضریب می‌تواند از (1-) تا (1) تغییر کند. مقدار مثبت بیانگر اینست که میزان انرژی تابشی در بالادست بیشتر از پایین دست است و مقدار منفی نیز بیان می‌کند که میزان انرژی تابشی در پایین دست بیشتر از بالادست است. البته در صورتیکه C صفر باشد می‌توان نتیجه گرفت که پراکندگی همگن است. در واقع C فاکتور تقارن محوری می‌باشد. در پیش‌فرض نرم‌افزار FLUENT نیز پراکندگی همگن در نظر گرفته شده است.

در معادله (11)، ترم f، اساسا کسر f از پراکنش خارجی (Out-Scaterring) را در معادله (10) حذف می‌کند. به عبارت دیگر برای f=1، عملکرد تابع فاز دلتای ادینگتون به گونه‌ای است که انگار اصلا پراکندگی وجود ندارد. هنگام استفاده از تابع دلتای ادینگتون لازمست مقادیر C و f مشخص گردد. هنگام استفاده از تابع تعریفی توسط کاربر (UDF) در نرم افزار Fluent، این نرم افزار تابع مذکور را در معادله (12) بکار می‌گیرد. تابع فاز پراکنش در دسترس برای تابش خاکستری می‌تواند برای تابش غیر خاکستری نیز استفاده شود. به هر صورت انرژی پراکنده شده، محدود به ماندن در پهنای باند مورد بررسی می‌باشد.

اثرات ذرات در مدل تشعشع DO

در استفاده از مدل DO می‌توان اثر فاز ثانویه گسسته متشکل از ذرات (در جریان‌های چند فازی) را بر انتقال حرارت تابشی لحاظ نمود. در چنین شرایطی از سایر منابع پراکنش در فاز گازی صرف نظر می‌شود. در نرم افزار Fluent نیز اینگونه می‌باشد. بطور کلی سهم فاز ذرات حاضر در معادلات RTE طبق معادله (13) تعیین می‌گردد.

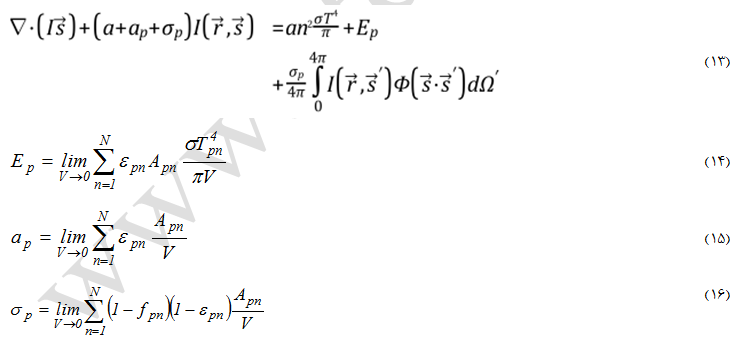
برای تابش غیر خاکستری جذب، انتشار و پراکنش ناشی از فاز ذره در پهنای باند هر طول موجی برای محاسبات تابش در نظر گرفته می‌شوند. لازم به ذکر است که ترم‌های جذب و انتشار ذرات در معادله انرژی نیز وارد می‌شود.

رفتار شرایط مرزی و نواحی پیوستگی در دیواره‌های مات

در مدل تشعشع DO امکان تعریف دیواره مات در هر کجای دامنه محاسباتی از جمله داخل دامنه، مرز بین نواحی سیال و جامد، مرز بین دو ناحیه جامد یا سیال و همچنین مرز بیرونی، وجود دارد. در شبیه سازی تابش خاکستری، دیواره‌های مات رفتاری شبیه جسم خاکستری از خود نشان می‌دهند. در شکل (6) شماتیکی از تابش روی دیواره مات در نرم افزار Fluent نشان داده شده است.

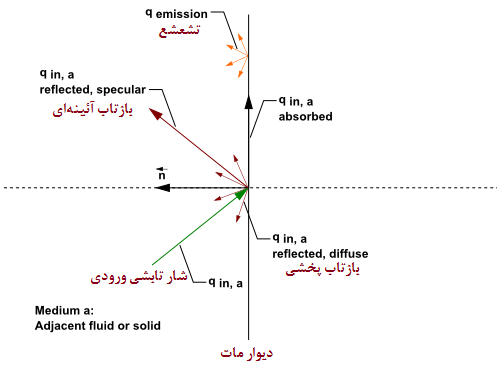
شکل-6: ویژگی‌های تابش روی دیواره مات در مدل DO

همانطور که در شکل فوق نشان داده شده، بخشی از انرژی تابشی ورودی، q_in,a، بصورت‌های آئینه‌ای (Specular) و پخشی (Diffuse) و بسته به کسر انتشار f_d در طرف a دیواره که توسط کاربر در شرایط مرزی دیواره مشخص می‌گردد، بازتابیده می‌شوند. بخشی نیز جذب دیواره می‌شود (Absorbed). از طرفی خود دیواره نیز دارای تشعشع (Emmision) بوده و بسته به قابلیت تشعشع (Emissivity) و کسر انتشار (Diffuse Fraction: f_d) انرژی از طح آن ساطع می‌شود. برای مدل‌های DO غیر خاکستری لازمست تشعشع داخلی برای هر باند طول موج مشخص گردد. قابل توجه است تابش از بین دیواره مات عبور نکرده و انتقال نمی‌یابد.

انرژی تابشی ورودی به دیواره می‌تواند به نواحی اطراف بازتاب یافته یا اینکه جذب آن شود. تابش بازتاب یافته می‌تواند بصورت پخشی یا آئینه‌ای (متمرکز)، بسته به کسر انتشار، f_d ، منعکس گردد. با فرض q_in به عنوان مقدار انرژی وارد بر دیواره مات، مقادیر عمومی محاسبه شده برای دیواره مات در نرم افزار Fluent عبارتند از:

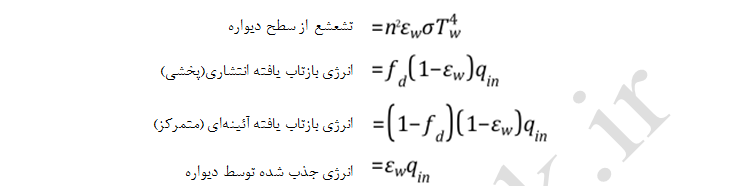
که f_d کسر انتشار، n ضریب شکست، ε_w قابلیت تشعشع دیواره، σ ثابت استفادن بولتزمن و T_W دمای دیواره می‌باشد. باید توجه داشت، اگر چه نرم افزار Fluent از قابلیت تشعشع در محاسبات مقادیر پارامترهای تابشی استفاده می‌کند، اما از گزینه و قابلیتی برای نمایش نتایج آن‌ها در ماژول پس پردازش (Post-Processing) برخوردار نیست. برای محاسبه میزان جذب انرژی تابشی توسط دیواره، فرض بر اینست که ضریب جذب با ضریب تشعشع برابر است. برای یک دیواره کاملا انتشار دهند f_d =1 بوده و هیچ گونه انرژی انعکاسی آئینه‌ای وجود ندارد. بطور مشابه برای یک دیواره کاملا آئینه‌ای، f_d =0 بوده و بنابراین مقدار انرژی انعکاسی پخشی نیز صفر می‌باشد. تابع انتشار بین 0 و 1 بیانگر انرژی انعکاسی در هر دوصورت پخشی و آئینه‌ای است.

دیواره‌های خاکستری(Gray Diffuse Walls)

برای تابش انتشار خاکستری، شار حرارتی تابشی ورودی، q_in، در دیواره و شار حرارتی تابشی خروجی، q_out بصورت معادلات (17) و (18) تعریف می‌شوند. در این معادلات n ضریب شکست، ε_w قابلیت تشعشع دیواره، σ ثابت استفادن بولتزمن و T_W دمای دیواره می‌باشند. قابل توجه است این معادلات برای تابش آئینه‌ای با قابلیت تشعشع ε_w=0 نیز صادق هستند. شدت تابش خروجی از دیواره، I_O، در جهت بردار S نیز از رابطه (19) محاسبه می‌شود.

دیواره‌های غیر خاکستری

دسته مشخصی از معادلات وجود دارد که بطور خاص برای دیواره‌های مات غیر خاکستری بکار می‌روند. در این معادلات فرض بر اینست که قابلیت جذب با قابلیت تشعشع سطح دیواره با هم برابرند. برای تابش غیر خاکستری، شار حرارتی تابشی ورودی، q_in، در باند λΔ بر روی دیواره بصورت معادله (20) می‌باشد. شار حرارتی تابشی خروجی، q_out، در باند λΔ نیز همانند معادله (21) تعریف می‌شود. در این معادله ε_wλ قابلیت تشعشع دیواره در باند λΔ و F(n, λ, T) تابع توزیع پلانک هستند. روابط مذکور نشان می‌دهند که تشعشع برای هر باند تابش بصورت تابعی از دمای سطح منبع می‌باشد. نکته اخر اینکه شدت تابش مرزی خروجی برای تمام جهات بردار S طبق معادله (22) محاسبه می‌شود.

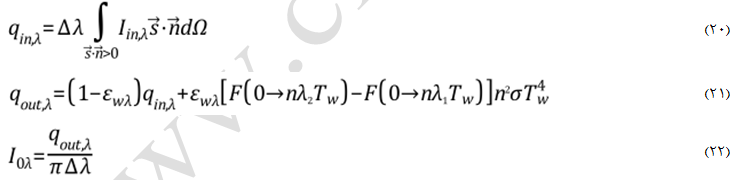
رفتار شرایط مرزی و دامنه محاسباتی در دیواره‌های نیمه شفاف

در نرم افزار Fluent می‌توان دیواره‌های نیمه شفاف داخلی و خارجی را برای مدل تشعشع DO تعریف نمود. در دیواره‌های نیمه شفاف داخلی تابش ورودی به دیواره می‌توان از آن گذشته و به نواحی مجاور برسد که به احتمال قریب به یقین با شکست پرتوها همراه است. همچنین پرتوها می‌توانند منعکس شده و یا در بین ضخامت دیواره جذب شوند. انتقال(Transmission) و انعکاس(Reflection) می‌توانند بصورت متمرکز (آئینه‌ای) و یا پخشی (انتشاری) باشند. لازمست برای تمام تابش‌های انتقالی و انعکاسی، کسر انتشار تعیین شده و برای باقیمانده رفتاری آئینه‌ای متصور شد. برای دیواره‌های نیمه شفاف خارجیف دو منبع احتمالی تابش بر روی دیواره محتمل می‌باشد. اول برخورد پرتوهای خارج از دامنه محاسباتی به سطح دیواره (مثل پرتوهای خورشید) و دوم تابش برخوردی به دیواره از المان‌های متشکل از از سیال یا جامد در داخل دامنه محاسباتی.

در تابش غیر خاکستری، شرایط مرزی دیواره غیر شفاف برای هر پهنای باند بصورت مجزا تعریف می‌شود. انرژی تابشی در هر باند انتقال(عبور همراه با شکست) یا انعکاس یافته و یا اینکه جذب آن می‌شود. باید توجه داشت که هیچ گونه جذب، انتقال و یا انعکاسی از یک باند به باند دیگر وجود ندارد. طبق پیش فرض نرم افزار Fluent، معادلات DO در ناحیه سیال و نه در ناحیه جامد حل می‌شوند. بنابراین در صورتیکه المان‌های مجاور به مرز دیواره، متشکل از ماده جامد باشند، لازمست ناحیه جامد را نیز در محاسبات لحاظ نمود. این عمل با انتخاب گزینه Participates In Radiation در فرم Solid، انجام می‌شود.

دیواره‌های داخلی نیمه شفاف

در شکل (7) شماتیکی از عملکرد یک دیواره داخلی دو طرف نیمه شفاف با ضخامت صفر در مقابل انرژی تابشی نشان داده شده است. انرژی تابشی برخوردی به دیواره که با q_in مشخص شده می‌تواند از دیواره شفاف عبور کند و بنابراین می‌توان آن را با معادله انرژی کوپل کرد. زمانی این کوپلینگ انجام می‌شود که دیواره نیمه شفاف تعریف شود. همانطور که در شکل زیر پیداست، انرژی تابشی برخوردی می‌تواند بصور متمرکز (Specular) و پخشی (Diffuse) از آن عبور کند. البته امکان بازتاب انرژی تابشی از دیواره داخلی به محیط اولیه نیز وجود دارد. اگر ضریب شکست دو طرف دیواره باه متفاوت باشد (n_a≠n_b)، آنگاه بازتابش نیز می‌تواند بسته به کسر انتشار، d_f، بصورت پخشی، متمرکز و یا ترکیبی از هر دو باشد. حالت‌های خاص انتقال یا بازتاب بصورت‌های پخشی خالص یا متمرکز خالص در دیواره‌های نیمه شفاف در ادامه معرفی می‌شود.

باید توجه داشت برای حالت‌های دیوراه‌های با ضخامت صفر، ضریب شکست دیواره روی بازتاب/انتقال پرتوها تأثیری ندارد و تنها ضریب شکست مواد تشکیل دهنده محیط اطراف مهم هستند. اگر دیواره‌های نیمه شفاف ضخامت داشته باشند آنگاه ضخامت و ضریب جذب آن‌ها، میزان قدرت جذب دیوراه نازک را تعیین می‌کنند. اگر ضخامت یا ضریب جذب دیواره صفر باشد، آنگاه دیواره دیگر قدرتی برای جذب انرژی تابشی ندارد.

**اگر چه انرژی تابشی در برخرود با دیواره نیمه شفاف دارای ضخامت می‌تواند جذب آن شود، اما پیش فرض آن در نرم افزار Fluent آنست که شار تابشی جذب شده روی معادلات انرژی تأثیری ندارد. در نتیجه شاهد عدم توازن انرژی و توزیع نامناسب دما خواهیم بود.

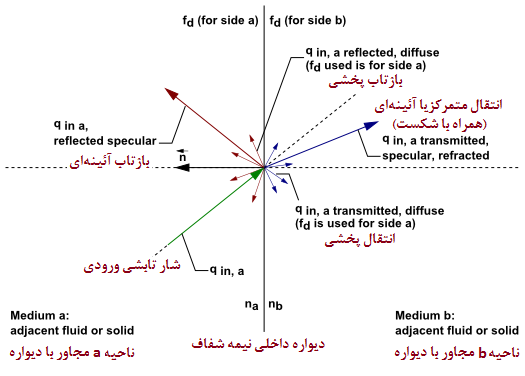
شکل-7: عملکرد یک دیواره داخلی نیمه شفاف در برابر انرژی تابشی.

در صورتیکه از شرط پوسته (Shell) استفاده شود، آنگاه کوپل کامل بین معادلات انرژی و تابش بوجود می‌آید. لازم به ذکر است شرط پوسته تنها برای مسائل سه بعدی در دسترس است. در شرایطی که دیواره دارای ضریب جذب/انتشار(تشعشع) قابل توجهی باشد، بهتر است کل دیواره بصورت یک ناحیه جامد مدلسازی شود. نرم افزار Fluent شامل گزینه تشعشع از سطح نیمه شفاف نمی‌باشد مگر آنکه شرط مرزی دما برای آن تعریف شود.

دیواره‌های نیمه شفاف آئینه‌ای (Specular Semi-Transparent Walls)

یک دیواره نیمه شفاف خاص را تصور کنید که کسر انتشار (پخش)، f_d،  آن صفر باشد و تمامی انرژی‌های انتقالی و انعکاسی آن از نوع آئینه‌ای (متمرکز) باشند. شکل (8) بیانگر پیمایش یک پرتو از ناحیه نیمه شفاف a با ضریب شکست n_a به ناحیه نیمه شفاف b با ضریب شکست n_b در جهت بردار S می‌باشد. در این شکل، سطح a در مرز مشترک به ناحیه a و بطور مشابه سطح b نیز به ناحیه b تعلق دارند.

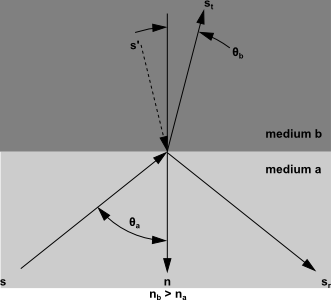
شکل-8: انعکاس و شکست پرتو در برخورد به دیواره نیمه شفاف آئینه‌ای.

همانطور که در شکل بالا پیداست، بخشی از انرژی برخوردی به فصل مشترک انعکاس یافته و باقیمانده نیز از آن عبور کرده و به ناحیه b انتقال پیدا می‌کند. بازتابش آئینه‌ای بوده بطوریکه جهت تابش انعکاس یافته با استفاده از معادله (23) مشخص می‌گردد. همانطور که گفته شد، تابش انتقال یافته از ناحیه a به ناحیه b با شکست پرتو همراه است. بنابراین جهت انرژی انتقال یافته طبق قانون اسنل (Snell’s Law) محاسبه می‌شود (معادله 24).

برای حالت n_a<n_b، انرژی انتقال یافته از ناحیه a به ناحیه b در زاویه ورودی 2π، راستای بردار n باید به طرف مخروط زاویه θ_c باشد (شکل-9). بطور مشابه اگر انرژی انتقال یافته از ناحیه b به ناحیه a در داخل مخروط زاویه θ_c باشد، پرتو انتقال یافته درناحیه a در جهت 2π (راستای بردار n) خواهد بود.

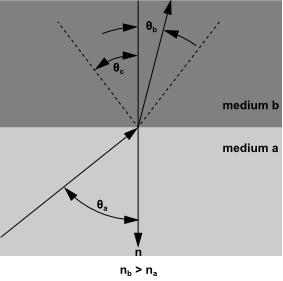
شکل-9: زاویه بحرانی θc.

برای زوایای برخورد θ_a بزرگتر از θ_c، انعکاس داخلی کل اتفاق می‌افتد و تمامی انرژی‌های ورودی بصورت متمرکز و آئینه‌ای در ناحیه b انعکاس می‌یابد. معادلات بیان شده در بالا را می‌توان برای حالت عمومی دیواره نیمه شفاف داخلی نشان داده شده در شکل (9) نیز بکار برد. موقعیکه ناحیه b همانند حالت دیواره نیمه شفاف خارجی، خارج از دامنه محاسباتی باشد (شکل-12)، شدت تابش مرزی در ناحیه b موجود در معادله (27) باید به عنوان یکی از ورودی‌های شرط مرزی دیواره، مشخص گردد. قابل توجه است که ضریب شکست در خارج از دامنه محاسباتی 1 فرض می‌گردد.

دیواره‌های نیمه شفاف پخشی (Diffuse Semi-Transparent Walls)

در نظر بگیرید که کسر انتشار (پخشی) یک دیواره نیمه شفاف یک باشد، f_d=1. در این حالت تمامی انرژی انتقال یافته یا منعکس شده تماما از نوع پخشی هستند. در بسیار از مسائل مهندسی، فصل مشترک نیمه شفاف ممکن است یک رفلکتور پخشی (Diffuse) باشد. برای چنین حالتی قابلیت انعکاس بین وجهی وابسته به بردار S و برابر با مقدار متوسط نیمکره r_d می‌باشد. برای n=n_a/n_b>1، روابط زیر حاکم است:

موقعی که ناحیه b همانند یک دیواره نیمه شفاف بیرونی، خارج از دامنه محاسباتی فرض می‌شود (شکل-10)، شار حرارتی q_in,b باید به عنوان یک مقدار ورودی مشخص گردد.

دیواره‌های نیمه شفاف شبه پخشی (Partially Diffuse Semi-Transparent Walls)

زمانیکه ضریب پخش f_d مشخص شده برای یک دیواره بین 0 و 1 باشد. دیواره هر دو رفتار پخشی و آئینه‌ای را از خود بروز می‌دهد. در این حالت لازمست هر دو مؤلفه پخشی و آئینه‌ای را برای انعکاس یا انتقال انرژی تابشی در محاسبات منظور نمود.

دیواره‌های خارجی نیمه شفاف (Semi-Transparent Exterior Walls)

شکل (10) حالت کلی پرتو تابشی q_irrad روی یک دیواره نیمه شفاف بیرونی با ضخامت و ضریب جذب صفر را نشان می‌دهد. برای کسب اطلاعات بیشتر در خصوص اثرات ضخامت دیواره بر کیفیت تابش بر دیواره نیمه شفاف، به بخش دیواره‌های داخلی نیمه شفاف مراجعه گردد.

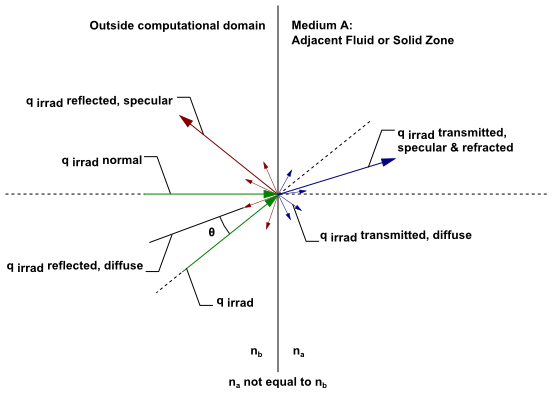
شکل-10: رفتار یک دیواره نیمه شفاف خارجی در برابر انرژی تابشی.

شار تابشی عبوری از دیواره از طرف بیرون دامنه محاسباتی به داخل دامنه محاسباتی متشکل از سیال یا جامد (ناحیه a) یا بالعکس را در نظر بگیرید. بسته به ضریب شکست و کسر پراکنش تعیین شده در شرایط مرزی، شار تابشی عبوری از دیواره می‌تواند بصورت پخشی یا متمرکز باشد. باید توجه داشت در صورتیکه ضریب شکست دیواره n_w برابر با یک نباشد، آنگاه یک مؤلفه انعکاسی نیز برای q_irrad وجود خواهد داشت. در نرم افزار Fluent اگر گزینه Mixed یا Radiation در بخش Thermal شرط مرزی Wall انتخاب شود، آنگار شار دیگری علاوه بر شار q_irrad و با عنوان Q_ext خواهیم داشت (معادله-36).

کسری از انرژی فوق که وارد دامنه محاسباتی می‌شود کاملا به میزان شفافیت دیواره نیمه شفاف وابسته است. قابل توجه است که انرژی در یک مخروطی توزیع شده و از رفتار پخشی (Diffuse) برخوردار است. پرتوها تابشی (Irradiation Beam) براساس اندازه، جهت و پهنا مشخص می‌شوند. مقدار تابش به فرم شار حرارت تابشی برخورد با واحد W/m² می‌باشد. پهنای بیم نیز بصورت یک مخروطی با زاویه مشخص (درصورتیکه تابش روی یک خط متمرکز نبوده و بشکل مخروطی باشد) تعریف می‌شود. پیش فرض نرم افزار Fluent برای پهنای پرتو  ^6-10 است که برای پرتو ورودی مناسب است. جهت بیم نیز توسط یک بردار عبوری از وسط زاویه بیم مشخص می‌گردد (شکل-11). 

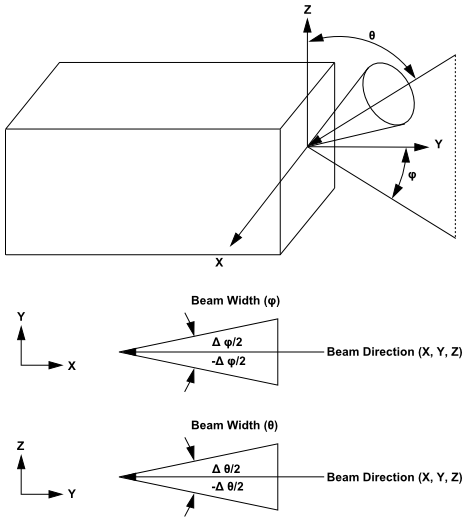
شکل-11: پهنا و جهت بیم در پرتوزدگی(Irradiation) خارجی.

اگر گزینه Apply Direct Irradiation Parallel to the Beam در کادر فرم شرط مرزی Wall در نرم افزار Fluent انتخاب شود، آنگاه با تعیین q_Irrad توسط کاربر، این نرم افزار بردار عمود بر سطح، q_Irrad.Normal را در محاسبات تابش، حل کرده و بکار می‌برد. در غیر اینصورت همان مقدار تعیین شده برای q_Irrad جایگزین q_Irrad.Normal می‌شود. شکل (13) شماتیکی از پهنا و جهت بیم را در پرتوزدگی(Irradiation) خارجی نشان می‌دهد. لازمست پارامترهای ورودی در این شکل بصورت شرط مرزی در یک دیواره نیمه شفاف مشخص شوند. بسته به ضریب شکست ناحیه a (که جزء خصوصیات ماده می‌باشد)، پرترو تابشی به این ناحیه دچار شکست می‌شود.

محدودیت‌ها

اگر شرط پوسته منظور نگردد، آنگاه نرم افزار Fluent در دیواره‌های نازک نیمه شفاف، محاسبات مرتبط با ضریب جذب/انتشار را منظور نمی‌کند. در چنین شرایطی اگر مقادیر جذب/تشعشع در مواد جامد دیواره قابل توجه باشد (مانند پنجره‌های شیشه‌ای در طول موج بلند)، استفاده از دیواره‌های نازک نیمه شفاف می‌تواند منجر به محاسبه غیر فیزیکی دما در حل عددی شود. اما با حل سه بعدی می‌توان بر این مشکل غلبه کرد. چراکه شرط پوسته تنها برای مدل‌های سه بعدی در دسترس می‌باشد. از طرف دیگر بهتر استدیواره‌ها بصورت صریح و کامل مدلسازی گشته و شبکه‌ای با حداقل یک ردیف المان در راستای ضخامت دیواره تولید شده تا شبیه سازی با دقت چشمگیر بیشتری انجام شود.

ناحیه نیمه شفاف جامد

با استفاده از مدل تشعشع DO می‌توان یک ناحیه جامد همجوار با نواحی جامد/مایع را به عنوان یک ناحیه نیمه شفاف مدلسازی نمود. این مهم به ما اجازه می‌دهد تا با حل معادله انرژی در این ناحیه، به جزئیات توزیع دما در آن برسیم. در نرم افزار Fluent، طبق پیش فرض، مدل DO تنها برای ناحیه سیال بکار می‌رود. بنابراین برای استفاده از این مدل در نواحی جامد لازمست آن را در فرم ناحیه پیوستگی Solid فعال کنیم (Cell Condition: Solid).

رفتار شرایط مرزی در دیواره‌های آئینه‌ای و مرزهای متقارن در مدل تشعشع DO

در دیواره‌های آئینه‌ای (Specular Walls) و مرزهای متقارن (Symmetry Boundaries)، اشعه بازتابیده در جهت بردار Sr متناظر با اشعه ورودی در جهت بردار S (معادله-37) می‌باشد. بنابراین در این نوع شرایط مرزی معادله زیر حاکم است.

رفتار شرط مرزی در مرزهای متناوب (پریودیک) در مدل تشعشع DO

موقع استفاده از شرط مرزی متناوب دورانی، کمیت پیکسل بندی برای محاسبه مناسب انرژی تابشی از مرهای پریودیک و سطوح سایه، بسیار حائز اهمیت است. در واقع پیکسل بندی بین 3*3 تا 10*10 پیشنهاد می‌گردد.

شرط مرزی در ورودی‌ها و خروجی‌ها در مدل تشعشع DO

در مدل تشعشع DO، ویژگی‌های مرزهای ورودی و خروجی همانند شرایط مرزی ورودی و خروجی در مدل تشعشع DTRM می‌باشد. برای کسب اطلاعات بیشتر به این صفحه مراجعه نمایید.

 

بازگشت

مطالب مرتبط

حل میدان‌های جریان‌های همراه با انتقال حرارت با استفاده از نرم‌افزارهای CFD

مبانی تئوری انتقال حرارت به روش هدایت و جابجایی

مدل تشعشعی DTRM

مدل تشعشع P-1

مدل تشعشع راسلند (Rosseland)

مدل تشعشع S2S

مدل تشعشع مونت کارلو (MC)

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ