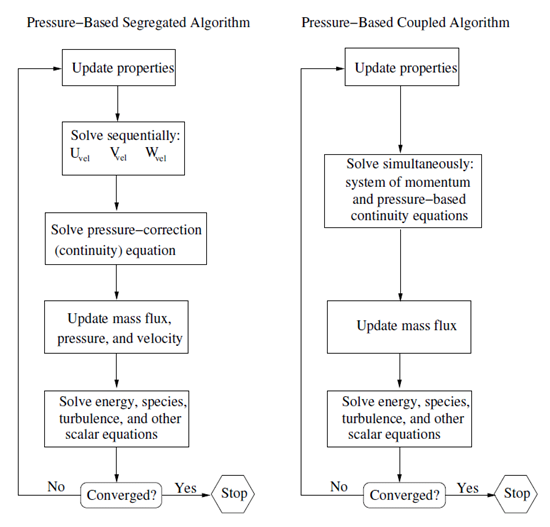
حلگر فشار مبنا (Pressure-Based)

حلگر فشار مبنا

Pressure-Based Solver

حلگر فشار مبنا (Pressure-Based) در کنار حلگر چگالی مبنا یکی از دو روش اصلی حل میدان جریان است. چگونگی گسسته‌سازی معادلات پیوستگی و ممنتم و همچنین نحوه حل آنها در حلگر فشار مبنا در این صفحه توضیح داده شده است. شکل ساده معادلات پیوستگی و ممنتم پایا و در فرم انتگرالی بصورت معادلات (1) و (2) هستند.

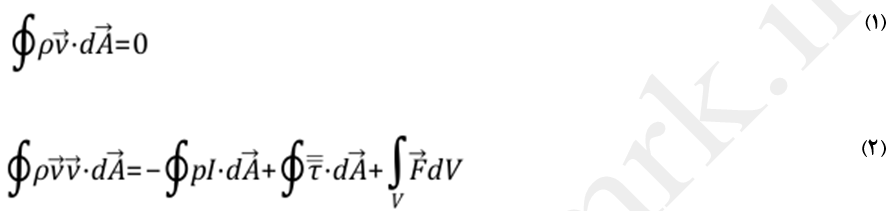
که I، ماتریس چگالی،

Ʈ، تانسور تنش و

F، بردار نیرو می‌باشد.

گسسته‌سازی معادله ممنتم در حلگر فشار مبنا (Pressure-Based)

روش گسسته‌سازی برای معادله انتقال اسکالر برای گسسته‌سازی معادلات ممنتم نیز بکار می‌رود. بنابراین می‌توان فرم گسسته شده معادله ممنتم در جهت x‌ را بصورت معادله (3)نوشت.

اگر میدان فشار و شار جرمی عبوری در هر یک از وجوه المان مشخص باشد، آنگاه معادله (2) را می‌توان با استفاده از روش‌های مختلف گسسته سازی حل کرد. به هر صورت در ابتدا، میدان فشار و دبی جرمی عبوری معلوم نبوده و باید بعنوان بخشی از مسئله بدست آید. به همین خاطر در نرم‌افزارهایی مانند FLUENT از روش هم-مکان(Co-Located Scheme) جاییکه، هر دو متغیر فشار و سرعت در مرکز المان بدست آمده، استفاده می‌کند. بطور کلی در معادله (3) لازمست که مقدار فشار در وجه بین المان‌ها معلوم باشد. بنابراین یک روش میانیابی برای محاسبه مقادیر فشار در هر وجه نسبت به مقادیر در مرکز المان مورد نیاز است.

روش‌های میانیابی فشار در حلگر فشار مبنا (Pressure-Based)

روش‌های متنوع و مختلفی برای میانیابی فشار توسعه یافته و مورد استفاده قرار می‌گیرند. مهمترین این روش‌ها که در نرم افزار Fluent نیز استفاده می‌شوند عبارتند از:

روش خطی

در این روش مقدار فشار در هر وجه از میانگین‌گیری مقدار فشار در المان‌های همسایه بدست می‌آید.

روش استاندارد

در این روش مقادیر فشار با استفاده از ضرائب محاسبه ممنتم میانیابی می‌شود (معادله 4). این روش تا زمانیکه تغییرات فشار بین مرکز المان‌ها هموار باشد، بخوبی کار می‌کند. زمانیکه که گرادیان ترم‌های چشمه معادله ممنتم بین المان‌ها زیاد باشد، گرادیان فشار در وجوه این المانها نیز زیاد بوده و نمی‌تواند با استفاده از این روش میانیابی شود. در حالت فوق اگر از روش یاد شده، استفاده شود، اختلاف سرعت بین مرکز المانهای همجوار بیش از مقدار معمول شده و موجب واگرائی حل می‌گردد. برای جریان‌هایی نظیر جریان چرخشی(Swiriling) قوی در جابجایی طبیعی با عدد ریلی بالا، لازمست که شبکه تولید شده در نواحی گرادیان فشار بالا از کیفیت مناسبی برخوردار بوده تا تغییرات فشار به درستی محاسبه شود.

در نرم‌افزارهایی همانند FLUENT، فرض شده که گرادیان فشار در جهت عمود بر دیواره صفر می‌باشد. این موضوع برای لایه‌های مرزی صادق است اما در حالت وجود نیروی وزن و انحنای دیواره نمی‌توان این فرض را بکار برد. بعلاوه عدم محاسبه دقیق گرادیان فشار در اندازه گیری بردارهای سرعت تأثیر می‌گذارد. بهمین خاطر در نرم‌افزر FLUENT، روشهای دیگری برای حالتهایی که میانیابی استاندارد فشار از کارایی لازم برخوردار نیست، نیز در نظر گرفته شده است.

روش مرتبه دوم

در این روش ترم‌های جابجایی فشار وجوه با استفاده از گسسته سازی دقت مرتبه دوم تفاضل مرکزی (Central Differencing) تصحیح می‌گردد (معادله 5). روش مذکور نسبت به روش استاندارد و مرتبه اول از کارایی نسبتاً بیشتری برخوردار است. اما ممکن است برای حالتهایی نظیر شروع محاسبات و یا دامنه محاسباتی متشکل از شبکه‌های با کیفیت پایین به مشکل برخورد کند.

برای جریان‌های شبیه سازی شده با مدل چند فازی اویلرین، بخاطر تغییرات زیاد احتمالی در خصوصیات جریان، روش مذکور کارایی ندارد. با این حال با ترکیب اثر گرادیان فشار روی فشار وجه (Face Pressure) المان‌ها، در معادله (5) و ترکیب آن‌ها با روش استاندارد (معادله 4)، روش مرتبه دوم برای مدلسازی جریان چند فازی با روش اویلرین در قالب معادله (6) تعریف می‌شود.برای مدلسازی جریان چند فازی به روش اویلرین در زمانیکه المان‌های شبکه از تعامد مناسبی برخوردار نباشند، روش مرتبه دوم تصحیح شده (معادله 6) نسبت به روش PRESTO! پایدارتر است.

روش نیروی وزنی(Body-Force-Weighted)

در این روش فشار وجوه با فرض اینکه گرادیان نرمال فشار ناشی از اختلاف بین فشار و نیروهای وزنی ثابت است، محاسبه می‌شود. این روش برای حالت‌هایی‌ که نیروهای وزنی در معادله ممنتم معلوم می‌باشد از کارایی خوبی برخوردار است (بعنوان مثال محاسبات گردابه متقارن و بویانسی). در موارد کسر حجمی چند سیالی ( Eulerian Multi-Fluid VOF) که نیروهای وزنی غالب هستند و المان‌های شبکه نیز از تعامد مناسب برخوردار نیستند، روش نیروی وزنی از روش {RESTO! پایدارتر است. در محیط‌های متخلخل (Porous Zone)، روش نیروی حجمی تنها برای وجوه غیر متخلخل اعمال می‌‍‌‌شود. در این روش ناپیوستگی نیرو‌های صریح حجمی (همانند گرانش، چرخش و کریولیس) و ناپیوستگی تغییرات فشار برای جریان‌های همراه با تغییرات شدید چگالی (مثل جابجایی طبیعی و تغییر ناگهانی فاز جریان از یک سیال به سیال دیگر) در نظر گرفته می‌شود.

روش (PREssure Staggering Option (PRESTO

روش فوق از بالانس پیوستگی گسسته برای یک حجم کنترل صلیبی (Staggered Control Volume) حول یک وجه برای محاسبه فشار آن وجه از المان استفاده می‌کند. این رویکرد همانند روش‌ شبکه صلیبی (Staggered Grd) قابل استفاده در شبکه‌های باسازمان می‌باشد. البته در نرم افزار Fluent روش مذکور برای تمامی شبکه‌ها قابل استفاده است. هر چند در نخه‌های قدیمی تنها برای شبکه‌‌‌‌های باسازمان با المانهای مربعی و مکعبی کاربرد داشت.

گسسته‌سازی معادله پیوستگی در حلگر فشار مبنا (Pressure-Based)

فرم گسسته معادله پیوستگی در قالب یک معادله اسکالر انتگرال گیری شده در یک حجم کنترل بصورت معادله (7) می‌باشد. در این معادله J_f شار جرمی از وجه f و معرف ρv_n  بوده و برابر ρv_nA_f می‌باشد.همانطور که اشاره شد، در روش‌های فشار مبنا (به جز روش Coupled) معادلات پیوستگی و ممنتم بطور متناوب حل می‌شود. در طی این فرآیند، معادله پیوستگی بعنوان یک معادله برای فشار استفاده می‌شود.

برای محاسبه مقادیر سرعت در هر وجه باید نسبت به مقادیر سرعت در مرکز المانها محاسبه شود. میانیابی خطی سرعتهای مرکز المانها برای وجوه بعنوان یک بررسی کننده غیر فیزیکی فشار می‌باشد. البته مقدار سرعت در روی وجوه از میانیابی خطی بدست نمی‌آید. بجای آن میانگین‌گیری وزنی ممنتم با استفاده از فاکتورهای وزنی و براساس ضریب a_p در معادله (3)، انجام می‌شود. که p_c0 و p_c2 مقدار فشار در المانهای مجاور هر وجه بوده و شامل تأثیر سرعت در این المانها می‌باشد. پارامتر d_f نیز تابعی از مقدار میانگین a_p  است.

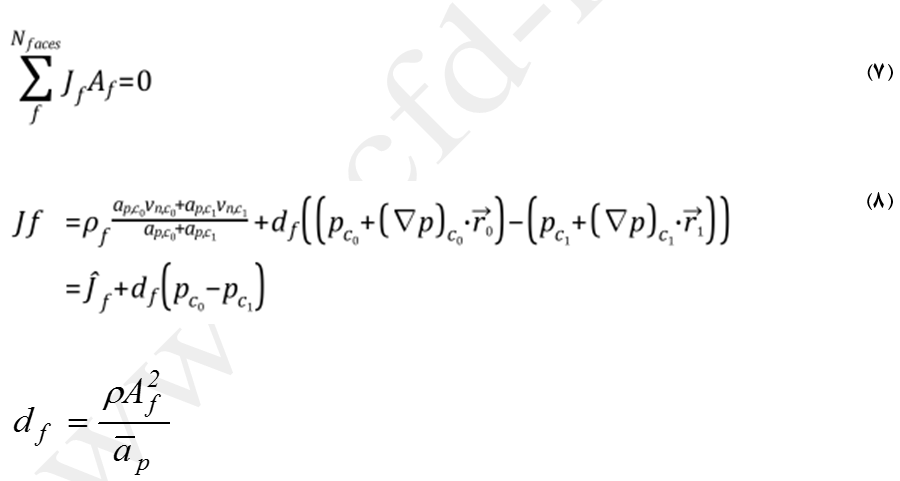
کوپلینگ سرعت-فشار (روش مجزا Segregated) در حلگر فشار مبنا (Pressure-Based)

کوپلینگ متغیرهای فشار و سرعت با استفاده از معادله (8) برای بدست آوردن یک معادله فشار از معادله پیوستگی گسسته‌شده (معادله 7)، حاصل می‌شود. نرم افزار CFX تنها از روش کوپله (Coupled) بهره می‌برد. در حالیکه در نرم افزار Fluent هر دو روش کوپله و مجزا (Segregated) قابل استفاده است. الگوریتم‌های SIMPLE، SIMPLEC و PISO مهمترین الگوریتم‌های روش مجزا برای کوپلینگ متغیرهای فشار و سرعت می‌باشند که در نرم افزار Fluent در دسترس هستند. در حل جریان‌های ناپایا متدهای پیشرفت زمان غیر تکراری (Non-Iterative Time Advancement Scheme: NITA) و گام کسری (Fractional Step Method: FSM) مطرح می‌باشند. لازم به ذکر است تمامی موارد فوق بجز روش کوپله براساس مفهوم پیش بینی پیشگو-تصحیحگر (Predictor-Corrector) توسعه یافته‌اند.

الگوریتم Semi-Implicit Method for Pressure Linked Equations: SIMPLE

از الگوریتم SIMPLE برای ارتباط بین تصحیحات سرعت و فشار بمنظور ارضاء کردن قانون بقای جرم و دست‌ یافتن به میدان فشار استفاده می‌شود. اگر معادله ممنتم با حدس اولیه میدان فشار ، حل شود، در نتیجه شار عبوری از وجوه محاسبه شده در معادله (8، معادله پیوستگی را ارضاء نمی‌کند. بهمین خاطر یک پارامتر تصحیح، J’_f، به پارامتر J^*_f اضافه شده تا شار عبوری از وجوه تصحیح گردد. پارامتر J’_f با استفاده از رابطه (11) محاسبه می‌شود. قابل توجه است در معادله (20-9) پارامتر فشار تصحیح شده هر المان می‌باشد. در الگوریتم SIMPLE، معادلات تصحیح شار (معادلات10 و 11) جایگزین معادله پیوستگی گسسته‌شده (معادله 7) شده تا یک معادله گسسته‌شده برای تصحیح فشار در هر المان، ‘p، بدست آید (معادله 12). ترم چشمه b در معادله (12) نرخ جریان خالص عبوری از المان بوده و با استفاده از معادله (13) محاسبه می‌شود. معادله تصحیح فشار (معادله 12) را می‌توان با استفاده از روش Algebraic Multigrid: AMG  حل کرد. راه حل دیگر اینست که فشار المان و نرخ جریان عبوری از وجوه با استفاده از معادلات (14 و 15) تصحیح گردد. در معادله (15)، α_p پارامتر Under-Relaxation برای فشار است. نرخ تصحیح شده جریان عبوری از هر وجه، J_f ، معادله پیوستگی گسسته‌شده را در هر تکرار ارضاء می‌کند.

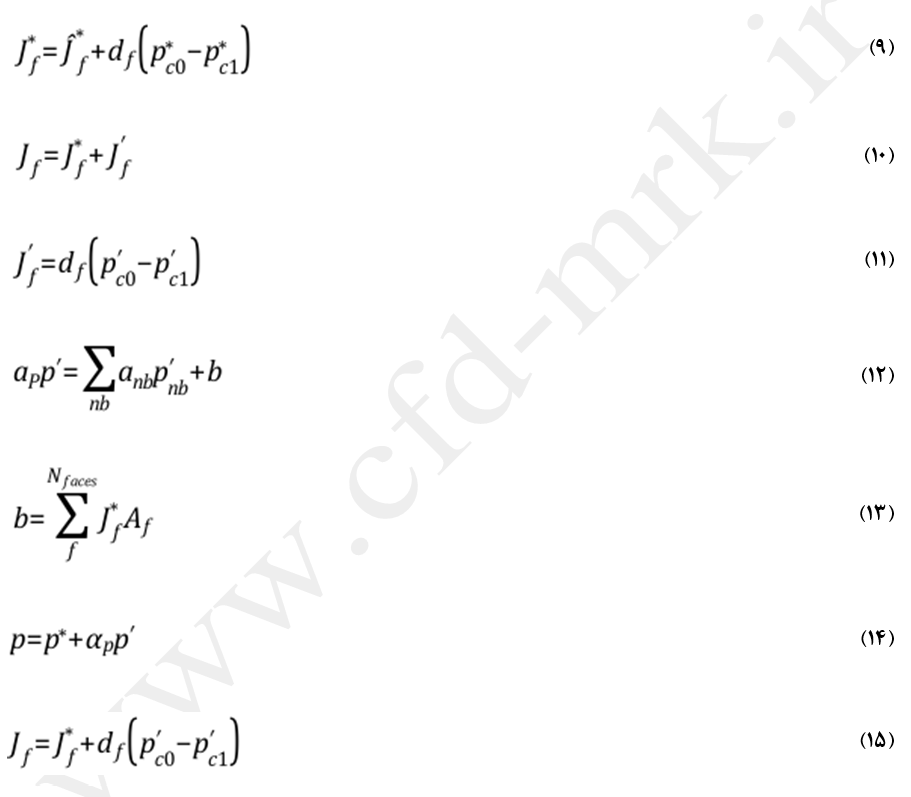
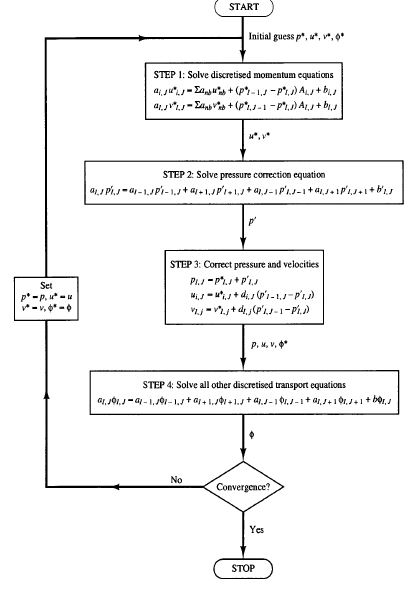
 الگوریتم SIMPLE

روش SIMPLEC

انواع مختلفی از الگوریتم SIMPLE، در ادبیات CFD موجود است. اگر چه در نرم‌افزار FLUENT، روش SIMPLE‌ بعنوان یک روش پیش فرض می‌باشد. اما پیشنهاد می‌شود که بجای این الگوریتم از الگوریتم (SIMPLEC(SIMPLE_Consistent، استفاده ‌شود چراکه در بسیاری از مسائل الگوریتم SIMPLEC از کارایی بهتری برخوردار است.

اساس الگوریتم SIMPLEC همانند الگوریتم SIMPLEمی‌باشد که در قسمت قبل توضیح داده شده است. تنها تفاوت بین این دو الگوریتم در سری بکار رفته برای تصحیح نرخ جریان عبوری از وجوه، J’_f، خلاصه شده است. همانند الگوریتم SIMPLE، معادله تصحیح کننده را می‌توان بصورت رابطه (16) نوشت. در این رابطه پارامتر d_f از معادله (17) بدست می‌آید.

استفاده از معادله تصحیح کننده فوق موجب افزایش نرخ همگرائی در مسائلی که کوپلینگ سرعت-فشار جزء اصلی پیچیدگی مسئله است. خواهد شد.

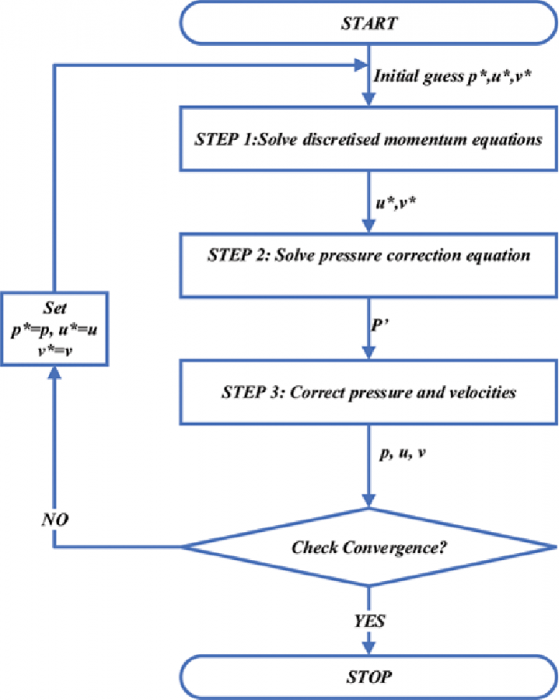
الگوریتم SIMPLEC

روش Pressure Implicit with Splitting Operators: PISO

روش PISO جزئی از خانواده الگوریتمهای SIMPLE بوده که براساس مرتبه بالاتر تقریب ارتباط بین تصحیحات فشار و سرعت توسعه یافته است. یکی از محدودیتهای الگوریتمهای SIMPLE و SIMPLEC اینست که پس از حل معادله تصحیح فشار، سرعتهای جدید و شارهای متناظر با آن نمی‌تواند معادله ممنتم را ارضاء کند. در نتیجه محاسبات آنقدر باید تکرار شود تا تعادل ممنتم برقرار گردد. برای بهبود اثر این محاسبات، الگوریتم PISO دو راهکار تصحیح همسایه(Neighbor Correction) و تصحیح تابیدگی(Skewness Correction) را پیشنهاد می‌کند. در ادامه هریک از دو راهکار مذکور توضیح داده شده است.

الگوریتم PISO

تصحیح همسایه

ایده اصلی الگوریتم PISO اینست که محاسبات تکراری مورد نیاز در الگوریتمهای SIMPLE و SIMPLEC را در مرحله حل معادله تصحیح فشار، وارد می‌کند. در این حالت همگرائی بسیار سریعتر صورت می‌گیرد. این فرآیند تکرار، تصحیح ممنتم یا تصحیح همسایه نامیده می‌شود. استفاده از الگوریتم PISO موجب افزایش نسبتاً کمی در زمان مورد نیاز برای هر تکرار شده اما تعداد تکرار برای دستیابی به همگرائی مورد نظر، بخصوص برای مسائل گذرا، را بطور چشمگیری کاهش می‌دهد.

تصحیح تابیدگی

برای شبکه‌های دارای المانهایی با تابیدگی غیر قابل اغماض، تقریب زدن برای تصحیح دبی جرمی عبوری از وجوه و اختلاف تصحیحات فشار در المانهای همسایه بسیار مشکل است. از آنجا که مؤلفه های گرادیان تصحیح فشار در امتداد وجوه المانها معلوم نیست، لذا استفاده از یک روش تکرار مشابه در الگوریتم PISO مناسب می‌باشد. پس از حل اولیه معادله تصحیح فشار، گرادیان تصحیح فشار برای بهینه کردن تصحیحات دبی جرمی وجوه، دوباره محاسبه می‌شود. این فرآیند که تصحیح تابیدگی نامیده می‌شود، بطور چشمگیری بر افزایش کیفیت همگرایی برای دامنه‌های محاسباتی شامل شبکه‌های بالمانهای دارای تابیدگی زیاد، تأثیر دارد. با استفاده از تصحیح تابیدگی الگوریتم PISO در نرم‌افزار FLUENT، همگرایی حل در دامنه‌های دارای شبکه‌های با المانهای دارایی تابیدگی زیاد، از کیفیت مناسبی برخوردار خواهد شد.

الگوریتم کوپله (Coupled) در حلگر فشار مبنا (Pressure-Based)

استفاده از روش کوپله نسبت به روش مجزا چند مزیت را به دنبال دارد. در روش کوپله شاهد پایداری و همگرایی بیشتر در حل میدان جریان بویژه یرای جریان‌های تک فاز و پایا هستیم. این روش به عنوان آلترناتیوی برای حلگرهای چگالی مبنا و همچنین فشار مبنای همراه با الگوریتم SIMPLE مطرح است. برای جریان‌های گذرا همراه با شبکه کم کیفیت، استفاده از این روش ضروریست. هم چنین با استفاده از روش مذکور می‌توان برای حل میدان جریان ناپایا گام‌های زمانی بزرگتری در نظر گرفت.

در رویکرد کوپله معادلات پیوستگی و ممنتم همزمان و همراه با هم حل می‌شوند. کوپلینگ کاملا ضمنی معادلات، از گسسته سازی ضمنی ترم‌های گرادیان فشار در معادلات ممنتم و شاره جرمی وجوه از جمله ترم‌های اتلاف فشار Rhie-Chow حاصل می‌شود. در معادلات ممنتم گرادیان فشار مؤلفه k بصورت رابطه (18) تعریف می‌شود. در این رابه aukp ضریب بدست آمده از واگرایی گاوس و روش درونیابی استاندارد فشار (معادله 4) می‌باشد. برای سلول iام، گسسته سازی معادلات ممنتم برای مؤلفه uk همان معادله (19) است. در معادله پیوستگی (7) تعادل شارها با استفاده از توصیف شارها در معادله (8)، جایگزین شده و رابطه (20) را نتیجه می‌دهد. در پایان فرم کلی معادلات (19 و 20) پس از انتقال به فرم δ در قالب معادلات (21) تا (24) بیان می‌شوند. تنها محدودیت روش کوپله در ناسازگاری آن با متد پیشرفت زمان غیر تکراری (Non-Iterative Time Advancement Scheme: NITA) خلاصه شده است.

بازگشت

مطالب مرتبط

حل میدان‌های جریان‌های تراکم‌ناپذیر و تراکم پذیر با استفاده از نرم افزارهای CFD

معرفی حلگرهای فشار مبنا و چگالی مبنا

حلگر چگالی مبنا (Density-Based)

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ