شرط مرزی رادیاتور

شرط مرزی رادیاتور

Radiator Boundary Condition

شرط مرزی رادیاتور برای مدل‌سازی یک رادیاتور در داخل دامنه محاسباتی به کار گرفته می‌شود. در واقع شرط مرزی مذکور برای محاسبه ضریب انتقال حرارت و افت فشار، بصورت تابعی از سرعت عمود بر رادیاتور به کار می‌رود.

معادلات رادیاتور

کاهش فشار و میزان انتقال حرارت رادیاتور در این شرط مرزی طبق مدل‌های زیر محاسبه می‌شود.

مدلسازی کاهش فشار در رادیاتور

در مدل رادیاتور، نرم‌افزار فلوئنت، رادیاتور را بی‌نهایت نازک فرض کرده و افت فشار درآن را متناسب با هد دینامیکی سیال و با استفاده از ضریب افت تعیین شده توسط کاربر، محاسبه می‌کند. تغییرات افت فشار،p∆، براساس مؤلفه عمودی سرعت،v ، بصورت رابطه (1) می‌باشد.

در رابطه (1) ρ چگالی سیال و k_L ضریب افت بدون بعد است. این ضریب بصورت یک عدد ثابت، چند جمله‌ای، تکه‌ای خطی و یا تکه‌ای چند جمله‌ای تعریف می‌شود. در حالت چند جمله‌ای،‌ k_Lطبق رابطه (2) محاسبه می‌گردد. در رابطه (2) r_n ضرائب چند جمله‌ای و v اندازه سرعت محلی عمود بر رادیاتور می‌باشد.

مدلسازی انتقال حرارت در رادیاتور

شار حرارتی از رادیاتور به سیال اطراف با استفاده رابطه زیر به دست می‌آید:

q شار حرارتی،

T_extدمای مبدل حرارتی (رادیاتور)

T_air,d دمای سیال خروجی می‌باشد.

همچنین در رابطه (3)، ضریب انتقال حرارت جابجایی می‌تواند بصورت یک عدد ثابت، یک تابع چندجمله‌ای، تکه‌ای خطی و یا تکه‌ای چند جمله‌ای در نظر گرفته شود. در فرم تابع چند جمله‌ای ضریب انتقال حرارت جابجایی براساس رابطه (4) بدست می‌آید.

در این رابطه h_n ضرائب چند جمله‌ای و v اندازه سرعت محلی عمود بر رادیاتور(متر بر ثانیه) می‌باشد.

محاسبه ضریب انتقال حرارت

برای مدلسازی رفتار حرارتی رادیاتور، لازمست که ضریب انتقال حرارت، h، که تابعی از سرعت عبوری از رادیاتور می‌باشد، بدرستی تعریف شود. برای بدست آوردن تعریف مناسبی برای ضریب انتقال حرارت، رابطه تعادل حرارتی زیر در نظر گرفته شود:

رابطه (5) را می‌توان بصورت زیر باز نویسی کرد:

ورودیهای شرط مرزی رادیاتور

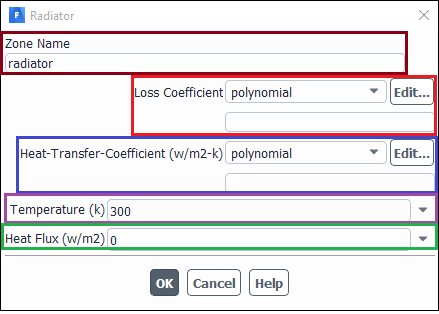
پس از مشخص کردن شرط مرزی رادیاتور، باید تمام پارامترهای ورودی این شرط مرزی در پانل Radiator بدرستی تعیین شود (شکل ابتدای صفحه). بطور کلی پارامترهای زیر در شرط مرزی رادیاتور مشخص می‌شود:

• ناحیه رادیاتور
• افت فشار در رادیاتور
• شار حرارتی و یا ضریب انتقال حرارت و همچنین دمای رادیاتور
• شرائط مرزی فاز گسسته (برای محاسبات فاز گسسته)

تعیین ناحیه رادیاتور

از آنجائیکه ضخامت رادیاتور بی‌نهایت نازک فرض می‌شود. لذا باید بعنوان فصل مشترک بین المان‌ها بجای ناحیه‌ای از المانها تعریف شود. بعبارت دیگر در نرم‌افزار فلوئنت، ناحیه رادیاتور در واقع از نوع ناحیه مرزهای داخلی می‌باشد. (لبه‌ها برای دو بعد و سطوح برای سه بعد).

تعیین افت فشار

برای تعریف افت فشار، k_L، لازمست که یکی از توابع ثابت، چند جمله‌ای، تکه‌ای خطی و یا تکه‌ای چند جمله‌ای براساس سرعت تعریف شده و یا اینکه ار توابع تعریف شده توسط کاربر استفاده شود.

 چگونگی تعریف افت فشار براساس تابع سرعت بصورت  چند جمله‌ای، تکه‌ای خطی و یا تکه‌ای چند جمله‌ای،  طبق مراحل زیر است:

1- یکی از گزینه‌های Polynomial، Piecewise-Linear و یا Piecewise-Polynomial (با توجه به نظر کاربر) در کادر فهرست Loss-Coefficient (شکل زیر) انتخاب شده و روی گزینه Edit کلیک شود.

2- پس از کلیک کردن روی گزینه Edit پانل مربوط به تعریف تابع (بعنوان مثال تابع چند جمله‌ای) باز می‌شود. در این پانل درجه چند جمله‌ای و ثابتها تعریف می‌شود. تعریف تابع محاسبه‌گر ضریب انتقال حرارت نیز به همین روش انجام می‌شود.

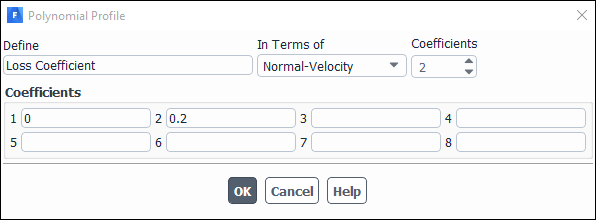
پانل Polynomial profile برای تعریف افت فشار.

مثال-1: محاسبه ضریب افت فشار

در این مثال چگونگی تعریف یک تابع برای افت فشار توضیح داده شده است. فرض بر اینست که جریان هوا با چگالی ثابت در یک کانال دوبعدی (شکل زیر) از بین یک رادیاتور خنک کننده آب، عبور می‌کند. خصوصیات رادیاتور باید بصورت تجربی مشخص شده باشد. در این مثال خصوصیات رادیاتور در جدول (1) براساس هد دینامیکی ورودی آب در رادیاتور با نرخی دبی جرمی 7 کیلوگرم بر دقیقه و دمای 400  درجه کلوین، درج شده است. برای محاسبه ضریب افت، از جدول (2) که براساس (معادله 1) تنظیم گردیده، استفاده شده است (چگالی هوا 1.0 کیلوگرم بر متر مکعب می‌باشد).

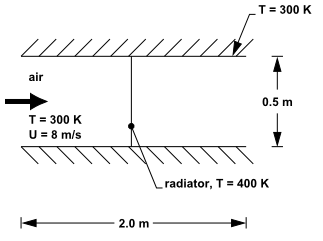
جریان عبوری از یک کانال دو بعدی مجهز به رادیاتور.

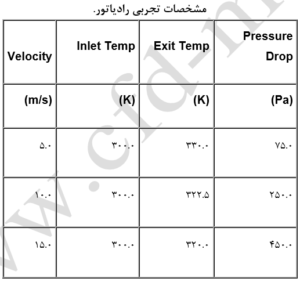
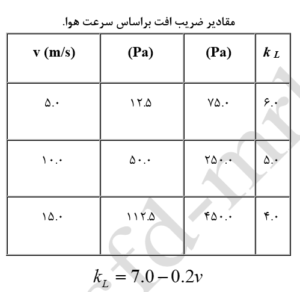
ضریب افت، تابعی خطی از سرعت می‌باشد که با افزایش سرعت، مقدار آن (طبق رابطه بالا) کم می‌شود. باید توجه داشت که در این رابطه فوق، v اندازه سرعت در رادیاتور می‌باشد.

مثال-2: محاسبه ضریب انتقال حرارت

در این مثال چگونگی تعریف یک تابع برای ضریب انتقال حرارت توضیح داده شده است. همانند مثال قبل، فرض بر اینست که جریان هوا با چگالی ثابت در یک کانال دوبعدی از بین یک رادیاتور خنک کننده آب، عبور می‌کند. خصوصیات رادیاتور باید بصورت تجربی مشخص شده باشد. در این مثال خصوصیات رادیاتور در جدول (1) براساس ورودی آب در رادیاتور با نرخی دبی جرمی 7 کیلوگرم بر دقیقه و دمای 400 درجه کلوین، درج شده است. (چگالی هوا 1.0 کیلوگرم بر متر مکعب و گرمای ویژه آب 1000، می‌باشد). با توجه به موارد فرض شده تغییرات ضریب انتقال حرارت براساس سرعت هوا در جدول (3) درج شده است.

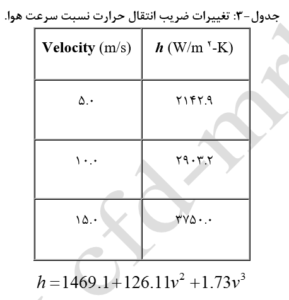
با توجه به مقادیر جدول فوق، می‌توان ضریب انتقال حرارت را بصورت یک تابع چند جمله‌ای درجه دوم نوشت. باید توجه داشت که در رابطه فوق، v، اندازه سرعت در رادیاتور می‌باشد.

بازگشت

مطالب مرتبط

شرط مرزی فن

شرط مرزی پرش متخلخل

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ