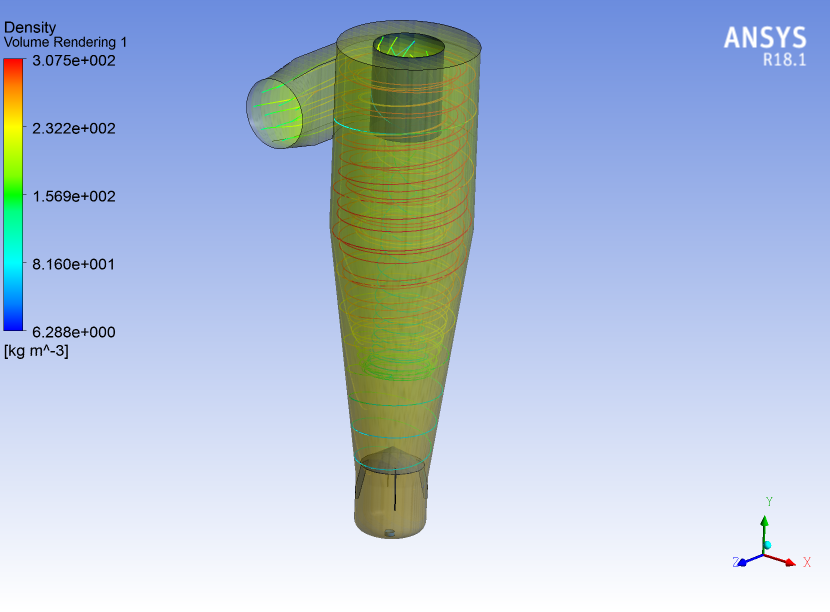
مدلسازی جریان چندفازی با استفاده از روش Mixture

Multiphase Flow Simulation Using Mixture Method

مدل Mixture یک مدل چند فازی ساده شده است که در موارد مختلفی بکار گرفته می‌شود. از این مدل می‌توان برای حل جریان‌ چند فازی با سرعت‌های مختلف هر یک از فازها استفاده نمود. البته در این حالت باید فرض تعادل محلی روی مقیاس‌های طول مکانی کوتاه در نظر گرفته شود. شبیه سازی جریان‌های چند فازی همگن با کوپلینگ بسیار بالا بین فازها در سرعت‌های یکسان یکی دیگر از موارد کاربرد این مدل است. در نهایت مدل Mixture ابزار مناسبی برای محاسبه لزجت غیر نیوتنی به شمار می‌رود. معادلات حل شده در مدل مذکور عبارتند از:

معادلات ممنتم، پیوستگی و انرژی برای جریان مخلوط.
معادله کسر حجمی برای فاز ثانویه.
یک رابطه جبری برای سرعت‌های نسبی.

کاربردهای عمومی این مدل شامل موارد زیر می‌باشد:

ته نشینی (Sedimentation).
جدا کننده‌های سیکلونی.
جریان‌های Particle Laden با بار کم.
جریان‌های حبابی که کسر حجمی گاز در آن کم باقی می‌ماند.

مدل Mixture گزینه بسیار مناسبی برای جانشینی مدل جامع اویلرین (Eulerian) برای برخی مسائل به شمار می‌رود. به عنوان مثال در هر یک از حالت‌های زیر امکان استفاده از مدل جامع اویلرین چندان مقدور نیست:

اگر توزیع گسترده‌ای از فازهای ذرات وجود داشته باشند (حجم محاسبات زیاد می‌شود).
قوانین بین فازها ناشناخته باشد.
قابلیت دوام (Reliability) و پایداری فازها حتمی نباشد.

مدل ساده‌تر Mixture در حل مسائل نسبت به مدل اویلرین پاسخ‌هایی با دقت مشابه با آن را به همراه دارد در حالیکه از متغیرهای کمتری استفاده می‌کند. همچنین در این مدل می‌توان فازهای ریگناک (Granular) را انتخاب کرده و تمام خواص آن را محاسبه نمود. این قابلیت برای برای حل میدان جریان‌های مایع-جامد قابل استفاده است.

1- محدودیت‌های مدل Mixture

در استفاده از مدل مذکور محدودیت‌هایی نیز وجود دارد که مهمترین آن‌ها در نرم افزار Fluent عبارتند از:

تنها با حلگر فشار مبنا (Pressure-Based ُSolver) قابل استفاده است. نمی‌توان آن را همراه با حلگر چگالی مبنا (Density-Based) بکار گرفت.
تنها یک فاز می‌تواند به عنوان گاز ایده‌آل تراکم پذیر تعریف شود. محدودیتی در تعریف مایعات تراکم پذیر با استفاده از توابع UDF در این نرم افزار وجود ندارد.
در هنگام استفاده از این مدل، امکان شبیه‌سازی جریان‌های پریودیک محوری با دبی جرمی مشخص وجود ندارد.
مدل ذوب و انجماد (Solidification and Melting) با مدل مورد بحث سازگار نبوده و نمی‌توانند همزمان استفاده شوند.
مدل کاویتاسیون سینگهال و همکاران (Singhal et al) در این مدل با مدل آشفتگی LES سازگار نیست.
امکان بکارگیری مدل مذکور در شبیه سازی جریان‌های غیر لزج (Inviscid) وجود ندارد.
مدل مورد بحث با احتراق پیش آمیخته، غیر پیش آمیخته و پیش آمیخته جزئی سازگار نیست.

این مدل همانند مدل VOF از تقریب تک سیالی (Single-Fluid) برای حل جریان‌های چند فازی استفاده می‌کند. البته با این تفاوت که:

در مدل مذکور امکان نفوذ و امتزاج فازها وجود دارد در حالیکه در مدل VOF اینگونه نیست.
در این مدل بخاطر استفاده از مفهوم سرعت لغزشی، سرعت نسبی بین فازها می‌تواند متفاوت و حتی بسیار زیاد باشد. این ویژگی در مدل VOF قابل شبیه سازی نیست.

2- معادله پیوستگی

معادله پیوستگی در مدل Mixture این گونه تعریف می‌شود. n معرف تعداد فاز است.

3- معادله ممنتم

معادله ممنتم برای جریان مخلوط کلی بصورت جمع معادلات ممنتم تک تک فازها (معادله 4) بدست می‌آید.

4- معادله انرژی

معادله حاکم بر انرژی جریان بصورت زیر می‌باشد:

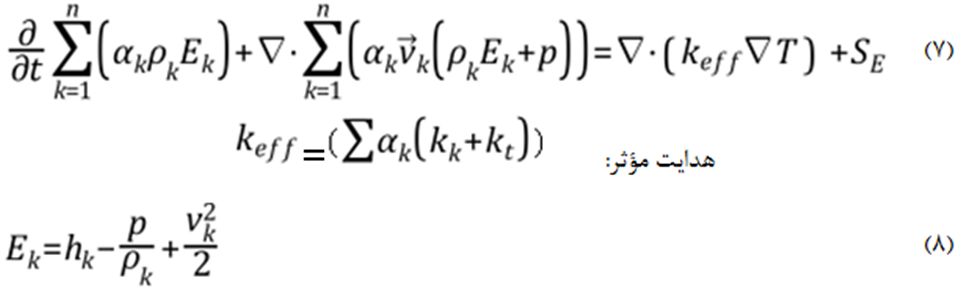
در معادلات فوق Kt هدایت گرمایی آشفته در جریان آشفته می‌باشد. ترم اول سمت راست معادله (7) بیانگر انرژی انتقال ناشی از هدایت است. در معادله مذکور، SE نیز معرف ترم‌های چشمه حرارتی حجمی تعریف شده توسط کاربر می‌باشد. برای جریان‌های تراکم پذیر معادله (8) و برای جریان‌های تراکم ناپذیر Ek=hk حاکم است. hk آنتالپی محسوس فاز k تعریف می‌شود.

5- سرعت نسبی (لغزشی) و سرعت دریفت (Relative (Slip) Velocity and Drift Velocity)

سرعت نسبی (لغزشی) بصورت سرعت فاز ثانویه p نسبت به فاز اصلی q (معادله 9) بیان می‌شود.

مدل Mixture موجود در نرم افزار Fluent از یک رابطه جبری برای سرعت نسبی استفاده می‌کند. فرض اصلی در این رابطه آنست که تعادل محلی بین فازها در مقیاس طولی کوتاه برقرار باشد. طبق تحقیقات مانینن و همکاران (Manninen et al) سرعت نسبی از رابطه (12) بدست می‌آید. ساده‌ترین فرمولاسیون سرعت نسبی جبری مدل فلاکس دریفت (ِDrift Flux) نام دارد. در این مدل شتاب ذرات از نیروهای گرانش و یا گریز از مرکز ناشی می‌شود. زمان آسایش ذرات (Particle Relaxation Time) بگونه‌ای تصحیح می‌گردد تا احتساب حضور سایر ذرات را در خود جای دهد. در جریان آشفته لازمست سرعت نسبی، حامل ترم انتشار حاوی پراکنش (Dispersion) موجود در معادله ممنتم برای فاز پراکنده نیز باشد. در نتیجه سرعت نسبی با استفاده از روابطه زیر محاسبه می‌شود.

در مدل Mixture موجود در نرم افزار Fluent می‌توان از فرمولاسیون متعددی برای محاسبه نیروی درگ استفاده نمود که عبارتند از:

رابطه پیش فرض نیومن-اشمیت (Schiller-Naumann).
مرسی-الکساندر (Morsi-Alexander)
متقارن (symmetric)
گریس و همکاران (Grace et al)
تامیاما و همکاران (Tomiyama et al)
قوانین درگ عمومی (universal drag laws)
ثابت (constant)
تابع قابل تعریف توسط کاربر (UDF)

اگر سرعت لغزشی در این مدل حل نشود، مدل مذکور بصورت یک مدل چند فازی همگن (Homogeneous) ساده می‌شود. همچنین در نرم افزار Fluent، با استفاده از UDF می‌توان توابع دلخواهی برای محاسبه سرعت لغزشی تعریف نمود.

6- معادله کسر حجمی برای فاز ثانویه

کسر حجمی فاز ثانویه p از طریق ح لمعادله پوستگی برای فاز p و بصورت زیر محاسبه می‌شود.

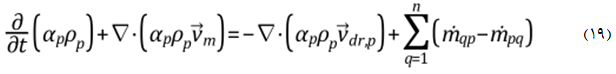
$mixture-volume-fraction$

7- خواص ریگناکی (Granular Properties)

غلظت ذرات در محاسبه سرعت مؤثر جریان مخلوط پارامتر مهمی است. از این رو ممکن است از مفهوم لزجت ریگناکی برای تعیین مقدار لزجت محلول استفاده شود. لذا لزجت متوسط حجمی شامل افزایش لزجت برشی بخاطر تغییر ممنتم ناشی از انتشار و تصادم ذرات نیز می‌شود. لزجت برشی ذرات جامد از لزجت تصادم (Collision)، جنبشی (Kinetic) و اصطکاکی (Friction) ذرات تشکیل می‌شود.

1-7: لزجت تصادم

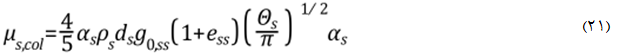
2-7: لزجت جنبشی

در نرم افزار Fluent از دو رابطه برای محاسبه لزجت جنبشی استفاده می‌شود. رابطه اول براساس تحقیق سیاملال و همکاران (Syamlal et al) و بصورت معادله (22) است. رابطه دوم نیز مبتنی بر بیان گیداسپاو و همکاران (Gidaspow et al) و طبق معادله (23) می‌باشد.

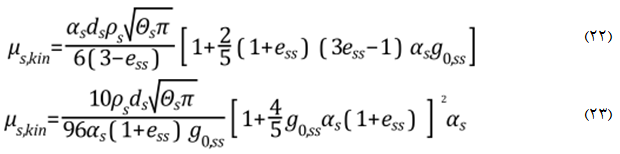
8- دمای ریگناکی در مدل Mixture

برای تعیین مقدار لزجت‌ها، دانستن دمای ریگناکی برای فاز جامد sام الزامیست. از این رو این دما از معادله انتقال دمای ریگناکی محاسبه می‌شود. این مهم تنها برای بسترهای شاره (Fluidized Beds) که در آن‌ها ترم‌های جابجایی و انتشار نسبت به انرژی ریگناکی تولید و اتلاف، قابل صرف نظر است بکار می‌رود.

اتلاف برخورد انرژی، γθs، بیانگر نرخ اتلاف انرژی در فاز جامد sام ناشی از برخورد بین ذرات است. رابطه معرف این ترم توسط لون و همکاران بصورت معادله (25) می‌باشد. انتقال انرژی جنبشی از نوسانات تصادفی در سرعت ذره از فاز جامد sام به فاز مایع یا جامد lام بصورت معادله (26) است.

در نرم افزار Fluent از یکی از سه روش زیر برای محاسبه دمای ریگناکی استفاده می‌شود.

فرمولاسیون جبری (پیش فرض

با حذف انتشار و جابجایی در معادله انتقال بدست می‌آید (معادله 24).

دمای ریگناکی ثابت

مناسب برای وضعیت‌های بسیار چگالی که نوسانات تصادفی در آن کوچک می‌باشد.

تعریف دمای ریگناکی با استفاده از UDF

9- فشار جامدات (Solids Pressure) در مدل Mixture

فشار جامد توتال در معادلات ممنتم لحاظ و محاسبه می‌گردد.

10- غلظت مساحت فصل مشترک (Interfacial Area Concentration)

غلظت مساحت فصل مشترک بصورت مساحت سطح تماس بین دو فاز بر واحد حجم مخلوط تعریف می‌شود. این مفهوم پارامتر مهمی برای پیش‌بینی جرم، ممنتم و انرژی انتقالی بین مرز مشترک فازها می‌باشد. در سیستم‌های دوفازی سیالی یکی فاز پیوسته و دیگری فاز گسسته لحاظ می‌گردد. در این سیستم‌ها، انداز و توزیع فاز گسسته می‌تواند بسرعت تحت تأثیر رشد (انتقال بین فازها)، انبساط ناشی از تغییرات فشار، انعقاد، شکست و یا مکانیزم‌های هسته‌ای تغییر کند. مدل تعادل جمعیت (population Balance Model) بطور تئوری این پدیده را شبیه سازی می‌کند. اما این مدل از لحاظ محاسباتی در زمانیکه به حل چندین معادله انتقال با استفاده از روش‌های ممان یا روش‌های گسسته نیاز باشد، بسیار گران است. مدل غلظت مساحت فصل مشترک از یک معادله انتقال برای هر فاز ثانویه استفاده می‌کند. مدل مذکور مختص شبیه سازی جریان‌های حبابی در سیال است. معادله انتقال برای غلظت بین سطحی بصورت زیر می‌باشد.

دو ترم اول سمت راست معادله (28) بیانگر انبساط حباب گاز در اثر تراکم پذیری و انتقال جرم (تغییر فاز) می‌باشد. دو دسته مدل هیبیکی-ایشی (Hibiki-Ishii) و ایشی-کیم (Ishii-Kim) برای ترم‌های چشمه و چاه غلظت مساحت فصل مشترک و براساس تحقیق ایشی و همکاران در دسترس است. طبق مطالعه آن‌ها، مکانیزم‌های اندرکنش فازها را می‌توان در 5 دسته زیر دسته بندی نمود.

انعقاد یا در هم آمیختگی (Coalescence) ناشی از برخورد تصادفی بخاطر آشفتگی جریان
شکست ناشی از ضربه گردابه‌های آشفته
به هم آمیختگی ناشی از ایجاد دنباله
برش گردابه‌های کوچک از گردابه‌های بزرگ
شکستن حباب‌های بزرگ در اثر ناپایداری سطح حباب

شکل زیر نشانگر مکانیزم‌های فوق می‌باشد.

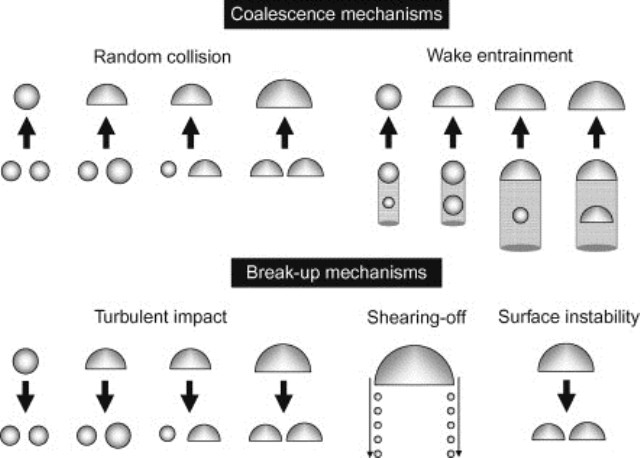
انواع مکانیزم‌های اندرکنش بین فازی در مدل Mixture.

در نرم افزار Fluent تنها سه اثر اولیه قابل شبیه سازی هستند.

1-10: مدل هیبیکی-ایشی

فرم کلی مدل بصورت زیر است:

**قابل توجه است مدلی برای SWE در فرمولاسیون هیبیکی-ایشی وجود ندارد.

2-10: مدل ایشی-کیم

مدل ایشی-کیم تنها برای جریان‌های دو فازی گاز-مایع و بصورت ستون حبابی مناسب است. فرمولاسیون کلی مدل مذکور بصورت زیر می‌باشد.

3-10: مدل یائو-مورل (Yao-Morel)

مساحت فصل مشترک حجمی (Volumetric Interfacial Area) پارامتر بسیار مهمی در محاسبه پدیده‌های تبادلی بین فازها می‌باشد. از جمله این پدیده‌های تبادلی می‌توان به ممنتم، جرم و انتقال حرارت اشاره نمود. در نرم افزار Fluent دو مدل بالا برای جریان‌های حبابی با انتقال جرم بالا بکار گرفته می‌شوند. بسطی برای این دو مدل موجود است که شامل اثرات انتقال جرم غیر همگن (Heterogeneous)روی دیواره می‌باشد. این مدل براساس تحقیقات مورل و یائو بوده و برای کاربردهای جوشش هسته‌ای مناسب است. انتقال مساحت فصل مشترک حجمی (معادله 28) شامل ترم ‌هسته‌ای و مدل‌هایی برای انعقاد و شکست می‌باشد. فرمولاسیون کلی مدل یاد شده در زیر نشان داده شده است.