مبانی تئوری آکوستیک

مبانی تئوری آکوستیک

The Theories Of Acoustics

مبانی تئوری آکوستیک براساس تولید، انتشار، شنیدن و اضمحلال صوت بنا نهاده شده است. صدا (Sound) در زبان انگلیسی، به معنی آن چیزی است که شنیده می شود. آکوستیک (Acoustic) نیز شاخه‌ای از فیزیک است که در مورد امواج مکانیکی در گازها، مایعات و جامدات بحث می‌کند. صدا را می توان در مراحل مختلفی مورد بررسی قرار داد. به عبارت دیگر، صدا از پیش از تولدش تا زمان از بین رفتنش مراحلی را طی می‌کند. هر مرحله، به طور تخصصی و به طور مجزا قابل بررسی است. صدا طی فرایندی ساده‌ای تولید، منتقل، شنیده و مضمحل می‌شود. هر کدام از این فرآیندها بحث‌های مفصلی را طلب می‌کند. 

علم آکوستیک در واقع به تولید، انتشار و اضمحلال صوت‌های هوابرد (Airborne) می‌پردازد. روش‌های عددی نیز شاخه‌ای از این علم را به خود اختصاص داده‌اند. همانطور که در اینجا اشاره شد، روش‌های عددی حل میدان آکوستیک عبارتند از:

• روش‌های مستقیم
• روش‌های انتگرالی
• روش‌های پهن باند

مبانی تئوری آکوستیک برای روش‌های عددی

روش‌های مستقیم فرمولاسیون جداگانه‌ای ندارند. در این روش‌ها سطح نویز براساس تغییرات متغیرهای جریان از جمله فشار نسبت به زمان، تعیین می‌شود. مهمترین و پرکاربردترین روش انتگرالی، روش فاکس-ویلیامز و هاوکینگز (Ffowcs-Williams and Hawkings: FW-H) می‌باشد که در این نوشتار به تفصیل تشریح شده است. روش‌های پهن باند اما متنوع‌تر هستند. مهمترین روش‌های پهن باند مورد بررسی قرار گرفته در اینجا عبارتند از:

• فرمولاسیون پرودمن (Proudman’s Formula)
• مدل منبع جت نویز (Jet Noise Source Models)
• مدل منبع نویز لایه مرزی (The Boundary Layer Noise Source Model)
• ترم‌های منبع در معادلات اویلر خطی شده
• ترم‌های منبع در معادله لایلی (Lilley’s Equation)

مبانی تئوری آکوستیک:

مدل فاکس-ویلیامز و هاوکینگز (FW-H)

معادله فاکس-ویلیامز و هاوکینگز (FW-H) یک معادله موج غیر همگن (Inhomogeneous) که با دستکاری و اصلاح معادلات پیوستگی و ممنتم ناویر-استوکس بدست می‌آید. این مدل بصورت معادله (1) تعریف می‌شود.

f=0 بیانگر مرز محاسباتی مورد نیاز برای جریان خارجی در فضای نامحدود (f>0) است که شرایط لازم برای استفاده از توابع عمومی و فضای آزاد گرین را به منظور حل مسئله فراهم می‌سازد. سطح f=0 با سطح منبع (انتشار) متناظر است. همچنین سطح مذکور می‌تواند بر سطح بدنه (نفوذ ناپذیر) یا سطح نفوذ پذیر جدا از بدنه همزمان شود. n_i نیز بردار نرمال واحد به سمت فضای خارج (f>0) می‌باشد. a_o سرعت صوت در دور دست (Far-Feild) و T_ij تنش لایت هیل (معادله-2) می‌باشد. P_ij تانسور تنش فشاری بوده و برای سیال استوکسی بصورت معادله (3) تعریف می‌شود. مقادیر جریان آزاد با زیر نویس o بیان می‌شوند.

معادله (1) تحت شرایط جریان در فضای آزاد و عدم وجود مانع بین منابع تولید نویز و گیرنده‌های صوتی، را می‌توان بصورت تحلیلی انتگرال گرفت. حل نهایی شامل انتگرال‌های سطح و حجم می‌باشد. انتگرال‌های سطحی مبین سهم منابع آکوستیک تک قطبی (Monopole) و دو قطبی (Dipole) و جزئی از منابع چهار قطبی (Quadrupole) می‌باشد. انتگرال‌های حجمی نیز معرف منابع چهار قطبی (حجمی)، در ناحیه‌ای خارج از سطح منبع هستند. سهم انتگرال‌های حجمی زمانیکه سرعت جریان زیر صوت و خیل کم بوده و همچنین سطح منبع نزدیک به ناحیه منبع باشد، کوچک می‌شود. در نتیجه معادله ساده شده (4)  برای تعریف فشار صوت ‘p حاصل خواهد شد.

توجه:

زمانیکه سطح انتگرال منطبق بر یک دیواره نفوذ ناپذیر باشد، دو ترم سمت راست معادله (4)، p’_T و p’_L به ترتیب به عنوان ترم‌های ضخامت و بارگذاری و براساس معانی فیزیکیشان مطرح می‌شوند.  براکت‌های معادلات (5) و (6) بیانگر این موضوع هستند که هسته‌های انتگرال در زمان‌های تأخیر، τ، (که بصورت تابعی از زمان گیرنده، t، و فاصله تا گیرنده، r، در معادله-9 تعریف می‌شوند) محاسبه می‌گردند. مقدار L_i نیز برابر با ضرب اسکالر L_iM_i می‌باشد. علامت دات روی متغیرهای معادلات فوق بیانگر تمایز زمان منبع از آن متغیرهاست.

برای محاسبه صدای آئرودینامیکی ناشی از جریان خارجی حول یک جسم لازمست اثرات همرفت (Convective Effects) لحاظ گشته و بردار سرعت جریان در دور دست V_conv  نیز مشخص شود. این گزینه معادل وضعیت تجربی همچون تست‌های پروازی (که در آن روی هواپیما میکروفون(ها) نصب می‌شود) و یا تست‌های تونل باد (که در آن میکروفون‌ها در هسته جریان تونل باد نصب می‌شوند) می‌باشد. در صورت اعمال شرایط همرفتی، محاسبه زمان تأخیر به مراتب پیچیده‌تر از معادله (9) خواهد بود. همانطور که در شکل (1) نشان داده شده است، سرعت انتشار صوت، a_θ، در نیمکره بالادست جریان بیشتر از a_o و در نیمکره پایین دست کمتر از آن می‌باشد. θ نیز جهت زاویه از بالادست به سمت گیرنده نصب شده است. طبق شکل (1) زمان تأخیر براساس معادله (10) محاسبه می‌شود. بدیهی است اثرات همرفتی تنها برای جریان‌های دور دست زیر صوت (V_conv<a_o) مفهوم دارد.

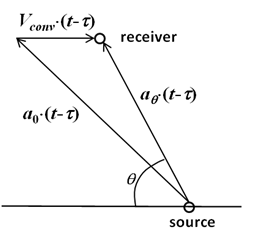
شکل-1: شماتیکی از اثر همرفت روی محاسبه زمان تأخیر

نکات مهم در استفاده از مدل FW-H

بطور کلی نکات مهم در بکار گیری مدل FW-H عبارتند از:

• در نرم افزار Fluent فرمولاسیون FW-H برای سطوح دورانی همچون سطوح ثابت قابل استفاده است.
• مهم نیست که سطح f=0 منطبق بر دیواره یا سطوح جسم باشد. فرمولاسیون FW-H به گونه‌ای است که بتوان سطح f=0 را در داخل دامنه نیز قرار داد.
• در زمانیکه سطح منبع صوت نفوذ پذیر (در داخل دامنه محاسباتی یا روی مرزهای اینترفیسی ثابت یا متغیر) در فاصله مشخصی، جدا از سطح جسم واقع شود آنگاه، حل‌های انتگرالی معادلات 5 و 6 در برگیرنده بخش‌هایی از منابع چهارقطبی در نواحی محصور به سطح منبع می‌باشند. البته در این شرایط، شبکه تولید شده باید به اندازه کافی ریز باشد تا بتواند ساختار جریان گذرا در داخل حجم محصور یا سطح نفوذپذیر را مدل کند.

مبانی تئوری آکوستیک:

مدل‌های منبع نویز پهن باند

برخلاف روش‌های مستقیم و انتگرلی FW-H، مدل‌های منبع نویز پهن باند (Boradband Noise Source Models) به حل گذرای معادلات حاکم بر جریان سیال احتیاجی ندارند. سرعت متوسط، انرژی جنبشی آشفتگی (k) و نرخ اتلاف آشفتگی (ε) مهمترین متغیرهای ورودی در برای تمامی مدل‌های پهن باند هستند. بنابراین مدل‌های آشفتگی معمول RANS برای شبیه سازی میدان جریان در منابع نویز پهن باند کافیست.

از آنجائیکه کنترل و کاهش نویز ایجاد شده توسط جریان مهمترین هدف در شبیه سازی آکوستیک است، از این مدل‌ها می‌توان برای تشخیص منبع (منابع) نویز استفاده کرد تا مشخص شود که کدام قسمت از جریان مهمترن نقش را در تولید نویز بازی می‌کند. البته توجه داشته باشید که این مدل‌ها، منبع صدا در گیرنده ها را پیش بینی نمی‌کنند.

چندین مدل منبع نویز پهن باند توسعه یافته است. این مدل‌ها به شما امکان می‌دهد سهم محلی (در واحد سطح یا حجم واحد) را به کل قدرت آکوستیک تولید شده توسط جریان تعیین کنید. در این نوشتار مهمترین مدل‌های موجود که در نرم افزار Fluent نیز مورد استفاده قرار می‌گیرند تشریح شده است.

مبانی تئوری آکوستیک:

فرمولاسیون پرودمن (Proudman’s Formula)

پرودمن با استفاده از قیاس آکوستیک (Acoustic Analogy) لایت هیل (Lighthill)، رابطه‌ای برای توان آکوستیک تولید شده توسط آشفتگی ایزوتروپیک بدون جریان میانگین استخراج نمود. بعدها لایلی (Lilley) براساس محاسبه تفاضل زمان تأخیر که در معادله پرودمن صرف نظر شده بود، رابطه جدیدتری ارائه کرد. هر دو رابطه معرف توان آکوستیک ناشی از آشفتگی ایزوتروپیک در واحد حجم می‌باشند (معادله 11).

در رابطه  (11) پارامترهای u و l به ترتیب سرعت آشفتگی و طول مشخصه هستند. در همین رابطه، a_o سرعت صوت و α ثابت مدل می‌باشد. براساس ترم‌های k و ε، معادله (11) بصورت روابط (12) و (13) بازنویسی می‌شود. ثابت α_ε با استفاده از حل DNS آشفتگی ایزوتروپیک برابر با 0.1 در نظر گرفته شده است. قابل توجه است توان آکوستیک را می‌توان درو احد dB (معادله 14) نیز تعیین کرد.

فرمول پرودمن مقدار تقریبی از سهم محلی توان کل آکوستیک بر واحد حجم در یک میدان آشته مشخص را بیان می‌کند. به هر صورت باید احتیاط لازم را هنگام تفسیر نتایج با توجه به مفروضات اتخاذ شده لحاظ نمود. این مفروضات شامل اعداد رینولدز بالا،  ماخ کوچک، ایزوتروپی آشفتگی و سرعت متوسط صفر می‌باشد.

مبانی تئوری آکوستیک:

مدل منبع جت نویز (Jet Noise Source Model)

این مدل منبع برای جت‌های متقارن محوری و براساس تحقیق گلدستین (Goldstein)  می‌باشد. در واقع مدل اصلی توسط ریبنر (Ribner) پیشنهاد شده بود. گلدستین مدل ریبنر را برای دستیابی به مقدار دقیقتر ناهمسانگردی (Anisotropy) آشفتگی در جت‌های آشفته متقارن محوری بهبود بخشید. در مدل گلدستین توان اکوستیک ساتع شده توسط حجم واحد جت آشفته و طبق معادله (15) محاسبه می‌شود.

رابطه (28) بیانگر بیان توان آکوستیک در واحد دسی بل (dB) می‌باشد.

مبانی تئوری آکوستیک:

منابع نویز لایه مرزی (The Boundary Layer Noise Source Model)

صدای دور دست تولید شده توسط جریان لایه مرزی روی یک بدنه جامد در اعدا ماخ پایین اغلب یکی از موضوعات مورد علاقه در مباحث تجربی است. انتگرال کرل (Curle) مبتنی بر قیاس اکوستیک می‌تواند برای تخمین سهم موضعی از سطح بدنه به توان کل آکوستیک، مورد استفاده قرار گیرد. انتگرال کرل طبق معادله (29) حساب می‌شود. با استفاده از معادله (29) می‌توان شدت صوت در دور دست را طبق رابطه (30) تخمین زد. توان کل آکوستیک ساتع شده از سطح کل جسم نیز با استفاده از معادلات (31) و (32) محاسبه می‌شود. معادله (32) به هر دو صورت ابعادی (W/M³) و dB قابل گزارش است.

مبانی تئوری آکوستیک:

ترم‌های منبع در معادلات اویلر خطی شده (Linearized Euler Equations: LEE)

معادلات اویلر خطی شده (LEE) می‌تواند از معادلات ناویر استوکس بدست آیند. این مهم با تجزیه متغیرهای جریان به پارامترهای متوسط، آشفتگی و آکوستیک امکان‌پذیر است. البته فرض بر اینست که مؤلفه‌های آکوستیک بطور قابل توجهی کوچکتر از مؤلفه‌های متوسط و آشفتگی می‌باشند. در نتیجه معادله اویلر خطی شده برای مؤلفه‌های سرعت آکوستیک طبق رابطه (33) نوشته می‌شود. در این رابطه زیر نویس a معرف مؤلفه‌های آکوستیک و بالا نویس پریم (‘) نیز معرف مؤلفه‌های آشفتگی هستند. ترم سمت راست معادله (33) را می‌توان به عنوان ترم‌های منبع مؤثر تولید نویز در نظر گرفت. طبق این ترم‌ها سه ترم اول درگیر ترم‌های آشفتگی بوده و بیشترین سهم را بخود اختصاص می‌دهند.

ترم‌های L_sh اغلب به منابع نویز برشی (Shear-Noise) دلالت دارند چراکه درگیر برش میانگین هستند. ترم L_se که تنها با مؤلفه‌های سرعت آشفته سروکار دارد نیز اغلب منبع نویز خودسر (Self-Noise) نامیده می‌شود. میدان سرعت آشفته مورد نیاز برای محاسبه ترم‌های منبع LEE با استفاده از روش تولید تصادفی و تابشی (Stochastic Noise Generation and Radiation) بدست می‌آید.  در این روش میدان سرعت آشفته و مشتقات آن از مجموعه N مود فوریه بدست می‌آید (معادله 34).

باید توجه داشت ترم‌های منبع در LEE مقادیر برداری بوده و بسته به ابعاد مسئله دارای دو یا سه مؤلفه می‌باشد.

مبانی تئوری آکوستیک:

ترم‌های منبع نویز در معادله لایلی (Lilley)

معادله لایلی یک معادله موج مرتبه سوم بوده که می‌تواند از ترکیب بقای جرم و ممنتم سیالات تراکم پذیر بدست آید. زمانیکه ترم‌های لزجت حذف شوند این معادله می‌تواند بصورت رابطه (35) نوشته شود. با جایگذاری معادله (36) در ترم چشمه معادله (35)، رابطه (37) استخراج می‌شود.

ترم‌های منبع تولید نویز در معادله (37) با استفاده از میدان سرعت متوسط و  مؤلفه‌های سرعت نوسانی حاصل از SNGR بدست می‌آیند. همچون ترم‌های منبع LEE، ترم‌های منبع معادله (37) به ترم‌های نویز برشی یا نویز خودسر دسته بندی و بصورت جداگانه قابل گزارش هستند.

 

بازگشت

مطالب مرتبط

شبیه سازی آکوستیک (نویز آئرودینامیکی) با استفاده از نرم افزارهای CFD

https://www.onera.fr/fr/actualites/propagation-acoustique-autour-dun-profil-a-trois-corps

برای کسب اطلاعات بیشتر با ما تماس بگیرید

محمدرضا کلیچ